一、什么是回归
回归的目的是预测数据型的目标值。最直接的办法是依据输入写出一个目标值的计算公式。加入你想要预测某位小姐姐男友汽车的功率大小,可能会这么计算:
小 姐 姐 男 友 汽 车 功 率 = 0.0015*男 友 年 薪 - 0.99* 收 听 公 共 广 播 时 间
这就是所谓的回归方程(regression equation),其中的0.0015和-0.99称作回归系数(regression weights),求这些回归系数的过程就是回归。一旦有了这些回归系数,再给的那个这些回归系数,再给定输入值,我们计算出回归系数与输入值的乘积之和,就可以得到最后的预测值。
二、线性回归
1. 简单线性回归
简单线性回归也叫一元线性回归,先来看一元线性方程:y = b + wx
这个直线方程相信大家都不陌生,这就是最简单的线性回归模型。其中,w是直线的斜率,b是直线的截距。

2. 多元线性回归

3. 线性回归的损失函数
损失函数是衡量预测值与真实值之间的差距的函数。这里采用平方误差作为线性回归的损失函数:


4. 简单线性回归的python实现
4.1 导入相关包
import numpy as np import pandas as pd import random import matplotlib as mpl import matplotlib.pyplot as plt plt.rcParams['font.sans-serif']=['simhei'] #显示中文 plt.rcParams['axes.unicode_minus']=False #用来正常显示负号 %matplotlib inline
4.2 导入数据集并探索数据
ex0 = pd.read_table('ex0.txt',header=None) ex0.head() ex0.shape ex0.describe()
4.3 构建辅助函数
def get_Mat(dataSet): """函数功能:输入DF数据集(最后一列为标签),返回特征矩阵和标签矩阵""" xMat = np.mat(dataSet.iloc[:,:-1].values) yMat = np.mat(dataSet.iloc[:,-1].values).T return xMat,yMat

def plotShow(dataSet): """函数功能:数据集可视化""" xMat,yMat=get_Mat(dataSet) plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5) plt.show()
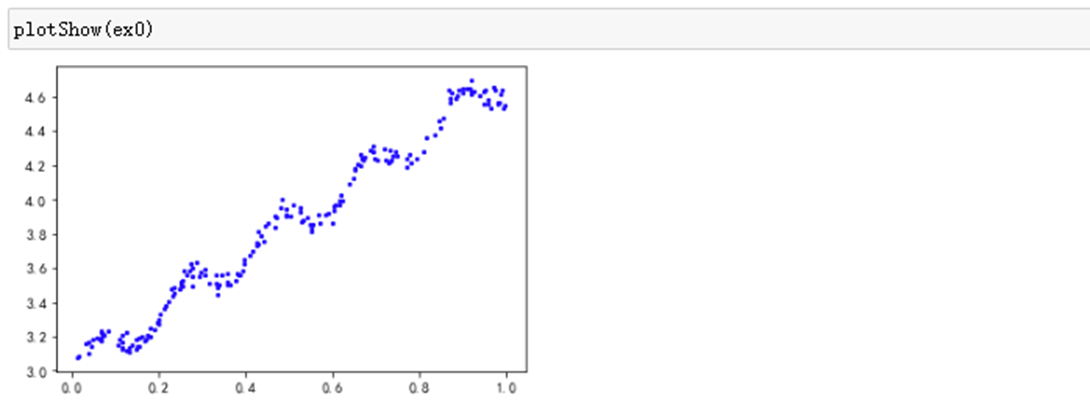
4.4 计算回归系数
def standRegres(dataSet): """ 函数功能:计算回归系数 参数说明: dataSet:原始数据集 返回: ws:回归系数 """ xMat,yMat =get_Mat(dataSet) xTx = xMat.T*xMat if np.linalg.det(xTx)==0: print('矩阵为奇异矩阵,无法求逆') return ws=xTx.I*(xMat.T*yMat) return ws

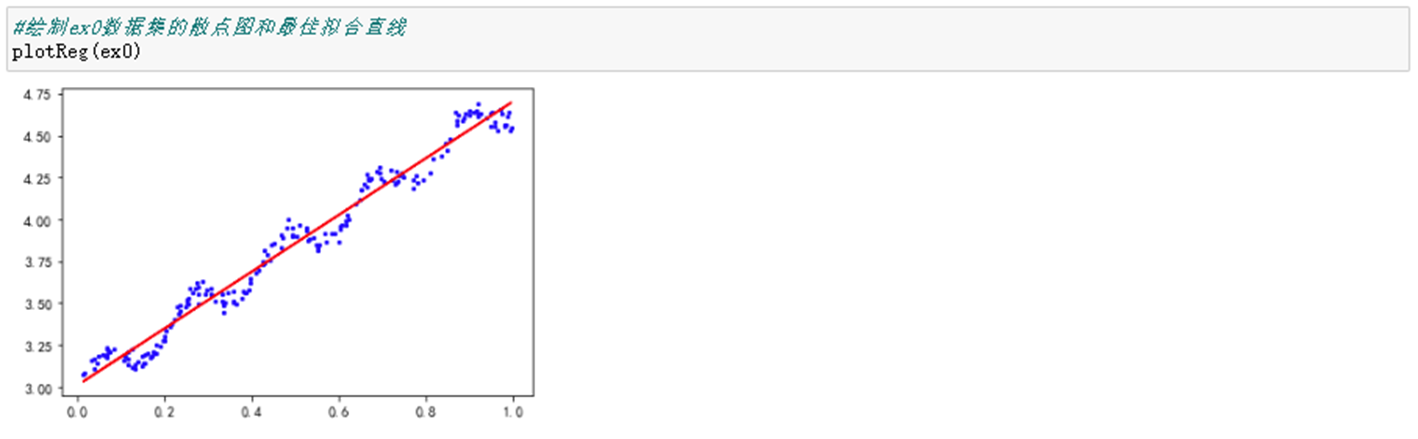
4.5 绘制最佳拟合直线
def plotReg(dataSet): """ 函数功能:绘制散点图和最佳拟合直线 """ xMat,yMat=get_Mat(dataSet) plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5) ws = standRegres(dataSet) yHat = xMat*ws plt.plot(xMat[:,1],yHat,c='r') plt.show()
4.6 计算相关系数
在python中,Numpy库提供了相关系数的计算方法:可以通过函数np.corrcoef(yEstimate, yActual)来计算预测值和真实值之间的相关性。这里需要保证的是,输入的两个参数都是行向量。

该矩阵包含所有凉凉组合的相关系数。可以看到,对角线上全部为1.0,因为自身匹配肯定是最完美的,而yHat和yMat的相关系数为0.98.看起来似乎是一个不错的结果。但是仔细关注数据集,会发现数据呈现有规律的波动,但是直线似乎没有很好的捕捉到这些波动。
三、局部加权线性回归
线性回归的一个问题时有可能出现欠拟合现象,为了解决这个问题,我们可以采用的一个方法是局部加权线性回归(Locally Weighted Linear Regreesion),简称LWLR。该算法思想就是给待预测点附近的每个店赋予一定的权重,然后按照简单线性回归求解w方法求解。与KNN一样,这种算法每次预测均需要实现选取出对应的数据子集。该算法解出回归系统w的形式如下:



#此段代码供大家参考 xMat,yMat = get_Mat(ex0) x=0.5 xi = np.arange(0,1.0,0.01) k1,k2,k3=0.5,0.1,0.01 w1 = np.exp((xi-x)**2/(-2*k1**2)) w2 = np.exp((xi-x)**2/(-2*k2**2)) w3 = np.exp((xi-x)**2/(-2*k3**2)) #创建画布 fig = plt.figure(figsize=(6,8),dpi=100) #子画布1,原始数据集 fig1 = fig.add_subplot(411) plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5) #子画布2,w=0.5 fig2 = fig.add_subplot(412) plt.plot(xi,w1,color='r') plt.legend(['k = 0.5']) #子画布3,w=0.1 fig3 = fig.add_subplot(413) plt.plot(xi,w2,color='g') plt.legend(['k = 0.1']) #子画布4,w=0.01 fig4 = fig.add_subplot(414) plt.plot(xi,w3,color='orange') plt.legend(['k = 0.01']) plt.show()

这里假定我们预测的点是x-0.5,最上面的图是原始数据集,从下面三张图可以看出随着k的减小,被用于训练集模型的数据点越来越少。
1. 构建LWLR函数
这个过程与简单线性函数的基本一致,唯一不同的是加入了权重weights,这里我将权重参数求解和预测yHat放在了一个函数里面。
def LWLR(testMat,xMat,yMat,k=1.0): """ 函数功能:计算局部加权线性回归的预测值 参数说明: testMat:测试集 xMat:训练集的特征矩阵 yMat:训练集的标签矩阵 返回: yHat:函数预测值 """ n=testMat.shape[0] m=xMat.shape[0] weights =np.mat(np.eye(m)) yHat = np.zeros(n) for i in range(n): for j in range(m): diffMat = testMat[i]-xMat[j] weights[j,j]=np.exp(diffMat*diffMat.T/(-2*k**2)) xTx = xMat.T*(weights*xMat) if np.linalg.det(xTx)==0: print('矩阵为奇异矩阵,不能求逆') return ws = xTx.I*(xMat.T*(weights*yMat)) yHat[i]= testMat[i]*ws return ws,yHat

2. 不同k值的结果图
我们调整k值,然后查看不同k值模型的影响。
xMat,yMat = get_Mat(ex0) #将数据点排列(argsort()默认升序排列,返回索引) srtInd = xMat[:,1].argsort(0) xSort=xMat[srtInd][:,0] xMat,yMat = get_Mat(ex0) #将数据点排列(argsort()默认升序排列,返回索引) srtInd = xMat[:,1].argsort(0) xSort=xMat[srtInd][:,0] #计算不同k取值下的y估计值yHat ws1,yHat1 = LWLR(xMat,xMat,yMat,k=1.0) ws2,yHat2 = LWLR(xMat,xMat,yMat,k=0.01) ws3,yHat3 = LWLR(xMat,xMat,yMat,k=0.003) #创建画布 fig = plt.figure(figsize=(6,8),dpi=100) #子图1绘制k=1.0的曲线 fig1=fig.add_subplot(311) plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2) plt.plot(xSort[:,1],yHat1[srtInd],linewidth=1,color='r') plt.title('局部加权回归曲线,k=1.0',size=10,color='r') #子图2绘制k=0.01的曲线 fig2=fig.add_subplot(312) plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2) plt.plot(xSort[:,1],yHat2[srtInd],linewidth=1,color='r') plt.title('局部加权回归曲线,k=0.01',size=10,color='r') #子图3绘制k=0.003的曲线 fig3=fig.add_subplot(313) plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2) plt.plot(xSort[:,1],yHat3[srtInd],linewidth=1,color='r') plt.title('局部加权回归曲线,k=0.003',size=10,color='r') #调整子图的间距 plt.tight_layout(pad=1.2) plt.show()
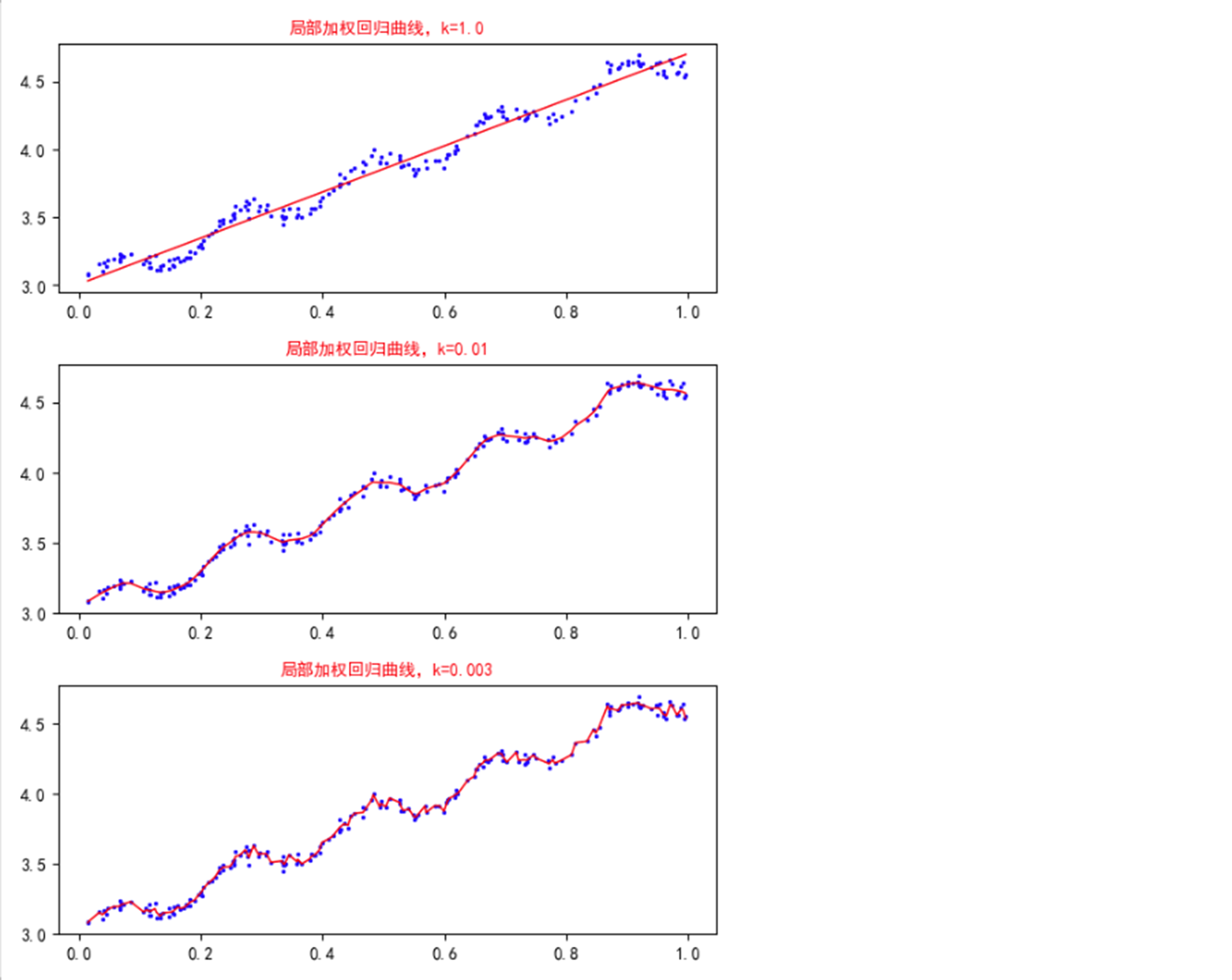
这三个图是不同平滑值绘制出的局部加权线性回归结果。当k=1.0时,模型的效果与最下二乘法差不多;k=0.01时,该模型基本上已经挖出了数据的潜在规律,当继续减小到k=0.003时,会发现模型考虑了太多的噪音,进而导致了过拟合现象。

局部加权线性回归也存在一个问题——增加了计算量,因为它对每个点预测都要使用整个数据集。从不同k值的结果图中可以看出,当k=0.01时模型可以很好地拟合数据潜在规律,但是同时看一下,k值与权重关系图,可以发现,当k=0.01时,大部分数据点的权重都接近0,也就是说他们基本上可以不用带入计算。所以如果一开始就去掉这些数据点的计算,那么就可以大大减少程序的运行时间了,从而缓解计算量增加带来的问题。
四、案例:预测鲍鱼的年龄
此案例所用数据来自UCL数据集,记录了鲍鱼(一种介可累水生生物)的一些相关属性,根据这些属性来预测鲍鱼的年龄。


1. 导入数据集
abalone = pd.read_table('abalone.txt',header=None) abalone.columns=['性别','长度','直径','高度','整体重量','肉重量','内脏重量','壳重','年龄']

从数据基本信息来看,并不存在缺失 NaN类型异常数据。
2. 查看数据分布状况
def dataPlot(dataSet): """ 函数功能:绘制散点图来查看特征和标签的数据分布 """ m,n=dataSet.shape fig = plt.figure(figsize=(8,20),dpi=100) colormap = mpl.cm.rainbow(np.linspace(0, 1, n)) for i in range(n): fig_ = fig.add_subplot(n,1,i+1) plt.scatter(range(m),dataSet.iloc[:,i].values,s=2,c=colormap[i]) plt.title(dataSet.columns[i]) plt.tight_layout(pad=1.2)
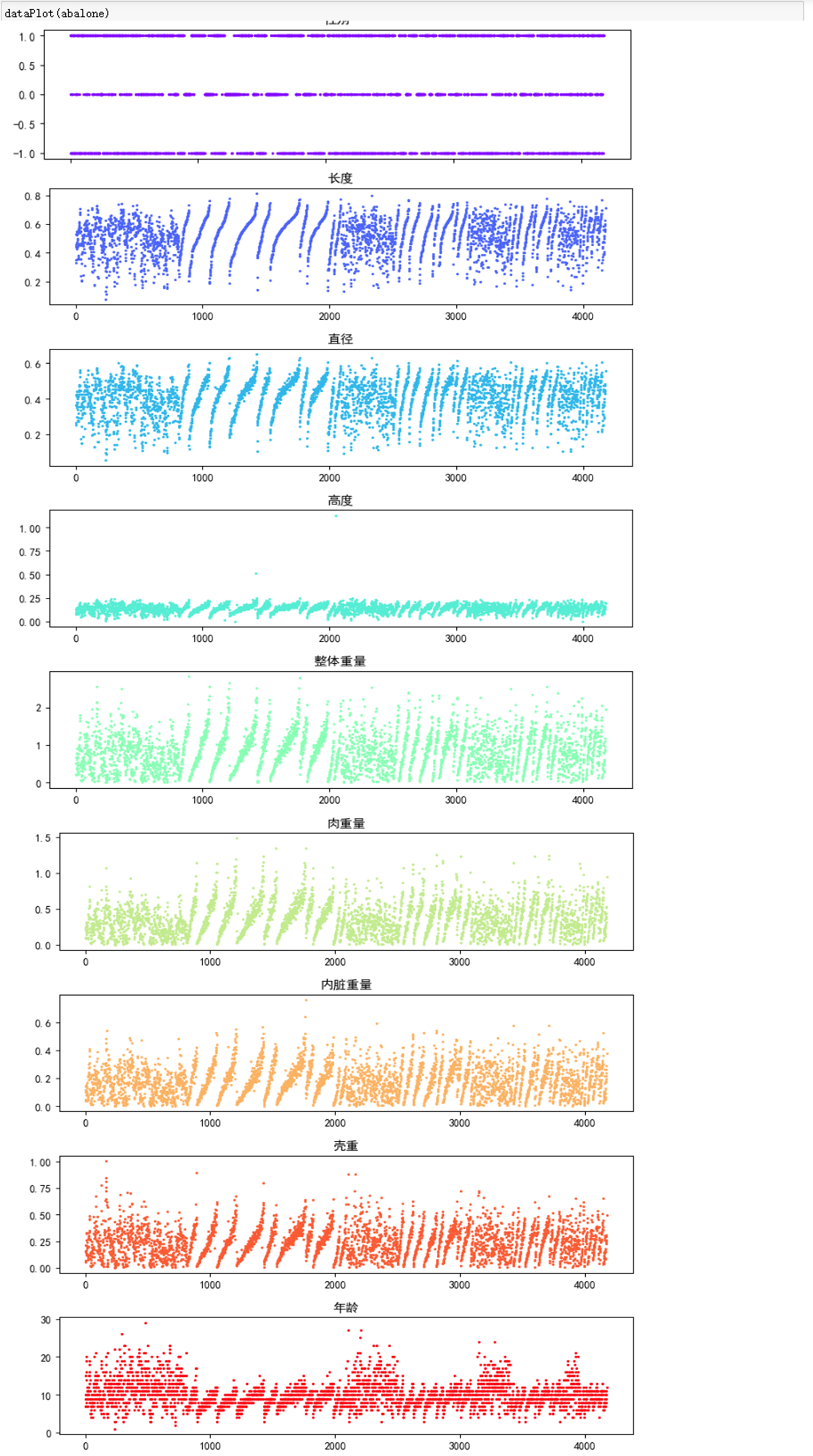
可以从数据分布散点图中看出:
①除“性别”之外,其他数据明显存在规律性排列;
②“高度”这一特征中,有两个异常值。
那从看到的现象,我们可以采取以下两种措施:
①切分训练集和测试集时,需要打乱原始数据集来进行随机调选;
② 剔除“高度”这一特征中的异常值

3. 切分训练集和测试集
此处采用train_test_split进行train与test切分。
from sklearn.model_selection import train_test_split # X数据集 Xdata = aba.iloc[:, :7] Xdata # y数据集 y = aba.iloc[:, 8:] y Xtrain, Xtest, Ytrain, Ytest = train_test_split(Xdata, y, train_size=0.8) train = pd.concat([Xtrain ,Ytrain], axis=1) train.head() test = pd.concat([Xtest ,Ytest], axis=1) test.head()
dataPlot(train)

dataPlot(test)

4. 构建辅助函数
def sseCal(dataSet, regres): """ 函数功能:计算误差平方和SSE 参数说明: dataSet:真实值 regres:求回归系数的函数 返回: SSE:误差平方和 """ xMat,yMat = get_Mat(dataSet) ws = regres(dataSet) yHat = xMat*ws sse = ((yMat.A.flatten() - yHat.A.flatten())**2).sum() return sse
以ex0数据集为例,查看函数运行结果:

def rSquare(dataSet,regres): """ 函数功能:计算相关系数R2 """ xMat,yMat=get_Mat(dataSet) sse = sseCal(dataSet,regres) sst = ((yMat.A-yMat.mean())**2).sum() r2 = 1 - sse / sst return r2
同样以ex0数据集为例,查看函数运行结果:

5. 构建加权线性模型
def ssePlot(train,test): """ 函数功能:绘制不同k取值下,训练集和测试集的SSE曲线 """ X0,Y0 = get_Mat(train) X1,Y1 =get_Mat(test) train_sse = [] test_sse = [] for k in np.arange(0.2,10,0.5): ws1,yHat1 = LWLR(X0[:99],X0[:99],Y0[:99],k) sse1 = ((Y0[:99].A.T - yHat1)**2).sum() train_sse.append(sse1) ws2,yHat2 = LWLR(X1[:99],X0[:99],Y0[:99],k) sse2 = ((Y1[:99].A.T - yHat2)**2).sum() test_sse.append(sse2) plt.plot(np.arange(0.2,10,0.5),train_sse,color='b') plt.plot(np.arange(0.2,10,0.5),test_sse,color='r') plt.xlabel('不同k取值') plt.ylabel('SSE') plt.legend(['train_sse','test_sse'])
运行结果:
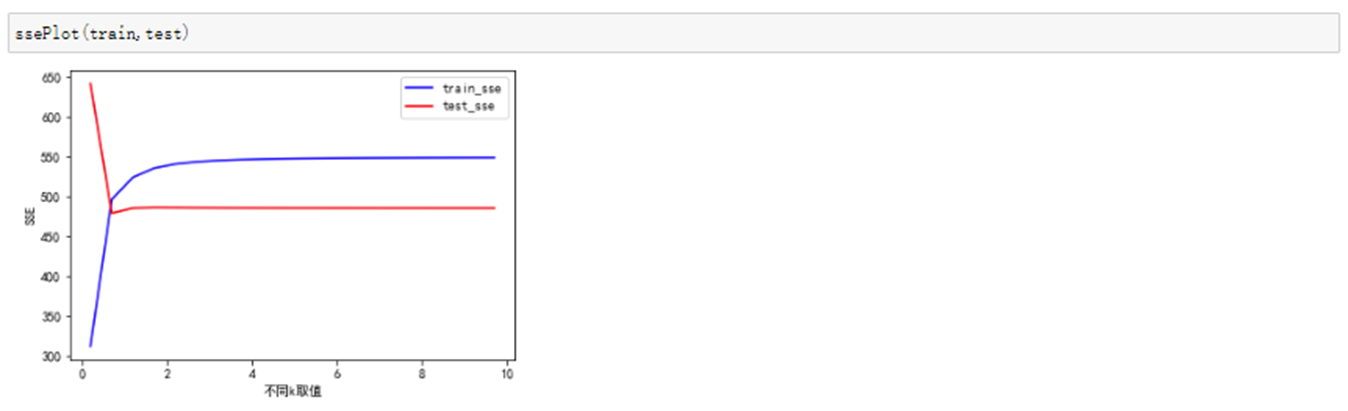
这个图的解读应该是这样的:从右往左看,当k取较大值时,模型比较稳定,随着k值的减少,训练集的SSE开始逐渐减小,当K取到2左右,训练集的SSE与测试的SSE相等,当K继续减少时,训练集的SSE也越来越小,也就是说,模型在训练集上的表现越来于浩,但是模型在测试集上的表现却越来越差了,这就说明模型开始出现过拟合了。其实,这个图与前面不同k值的结果图是吻合的,K=1.0,0.01,0.003这三张图也表明随着K的减小,模型会逐渐出现过拟合。所以这里可以看出,K在2左右的取值最佳。
再将K=2带入局部线性回归模型中,然后查看预测结果:

封装一个函数计算SSE和R方,方便后续调用
def LWLR_pre(dataSet): """ 函数功能:计算加权线性回归的SSE和R方 """ Xtrain, Xtest, Ytrain, Ytest = train_test_split(aba.iloc[:, :8], aba.iloc[:, 8:], train_size=0.8) train = pd.concat([Xtrain, Ytrain], axis=1) test = pd.concat([Xtest, Ytest], axis=1) trainX,trainY = get_Mat(train) testX,testY = get_Mat(test) ws,yHat = LWLR(testX,trainX,trainY,k=2) sse = ((testY.A.T - yHat)**2).sum() sst = ((testY.A-testY.mean())**2).sum() r2 = 1 - sse / sst return sse,r2
查看模型预测结果:

从结果可以看出,SSE近4000,相关系数只有0.47,模型效果并不是很好。
五、岭回归
在前面线性回归的求解过程中,我们使用最小二乘法来求解最优解,但是其中有一个隐形的条件:XTX的行列式|XTX| ≠ 0,也就是说必须要求XTX为满秩矩阵或者正定阵。
| 矩阵知识 | 矩阵知识点回顾(以非零m*n矩阵A为例) |
| 秩 |
矩阵A的列秩是A的最大线性无关列集合的大小,行秩是A的最大线性无关行集合的大小 对于任意矩阵A,其行秩等于其列秩,可以统称为秩 所以A的秩是【0, min(m,n)】内的整数 |
| 满秩 | 一个矩阵A的列满秩的,当且仅当该矩阵不存在空向量 |
| 正定矩阵 | 对于任意列满秩的矩阵A,矩阵ATA是正定的 |
1. 什么是岭回归
岭回归(Ridge Regression)是线性回归的一种进阶算法,它最先主要用来处理那种特征比样本点还多,也就是说,输入数据的矩阵X不是满秩矩阵的情况,现在也用于估计中加入偏差,从而得到更好的估计。岭回归的算法核心是:在矩阵XTX上加一个λI从而使得矩阵非奇异,进而能对XTX + λI 求逆。假如我们的数据集有m个样本点n个特征,回归系数的计算公式变为:

其中λ是一个人为定义的参数,矩阵I 是一个m*m的单位矩阵。对角线上全是1,其他元素全是0.
这里通过引入λ来限制了所有w之和,λ可称之为惩罚项,它能够减少不重要的参数,这个技术在统计学中也叫做缩减(shrinkage)。

2. 构建岭回归模型
岭回归函数,此处默认设置岭回归系数为0.2,当该系数部位0的时候不会存在不可逆的情况,因此可免去if语句判别是否满秩的设置。对于单位矩阵的生成,需要借助numpy中的eye函数,该函数需要数据对角矩阵规模参数。

def ridgeRegres(dataSet, lam=0.2): """ 函数功能:计算回归系数 参数说明: dataSet:原始数据集 lam:人为设定的惩罚系数(默认0.2) 返回: ws:回归系数 """ xMat,yMat=get_Mat(dataSet) xTx = xMat.T * xMat denom = xTx + np.eye(xMat.shape[1])*lam ws = denom.I * (xMat.T * yMat) return ws


从结果可以看出,两者效果差不多,那我们改变λ的值,看看回归系数如何改变。我们可以通过绘制岭迹图更直观的查看回归系数的变化。
3. 绘制岭迹图
这里需要对特征做标准化处理。因为,我们需要使每个维度特征具有相同的重要性。这里用了比较简单的标准化处理手段——所有特征都减去各自的均值并除以方差。
def ridgeTest(dataSet,k=30): """ 函数功能:计算岭回归的回归系数(默认λ以指数级变化) 参数说明: dataSet:原始数据集 k:λ的个数 返回: wMat:回归系数矩阵 """ xMat,yMat=get_Mat(dataSet) m,n=xMat.shape wMat = np.zeros((k,n)) #特征标准化 yMean = yMat.mean(0) xMeans = xMat.mean(0) xVar = xMat.var(0) yMat = yMat-yMean xMat = (xMat-xMeans)/xVar for i in range(k): xTx = xMat.T*xMat lam = np.exp(i-10) denom = xTx+np.eye(n)*lam ws=denom.I*(xMat.T*yMat) wMat[i,:]=ws.T return wMat
k与λ关系:

运行函数,查看结果:

通过岭迹图我们可以:
① 观察较佳的λ取值:通常取喇叭口的值,大家看岭迹图可以发现,当λ增大到某个值时,所有的回归系数开始发生变化,那这个λ值就是我们要找寻的较佳惩罚系数,此时准确率会比较高(前提是数据有线性关系),并且SSE比较小,模型泛化能力会比较好。
② 观察变量是否有多重共线性:随着λ的增加,回归系数会出现增大再减小的波动状况,则说明变量存在共线性,并且曲线交点越多说明共线性越强。

六、lasso
不难证明,在增加如下约束时,普通的最小二乘法回归会得到与岭回归一样的公式:

这个式子限定了所有回归系数的平方和不能大于λ。使用普通的最小二乘法回归,在有共线性或者多重共线性出现的情况下,可能会出现一个值很大的正系数或者负系数。正是因为这种限制条件的存在,使用岭回归可以避免这个问题。
与岭回归类似,另一个缩减方法LASSO(Least Absolite Shrinkage and Selection Operator)也对回归系数做了限定,对应的约束条件如下:

唯一不同的是,这个约束条件使用绝对值取代了平方和。虽然只是约束形式稍作变化,结果却大相径庭:在λ足够小的时候,一些系数会因此被迫缩减到0而岭回归却是很能使得某个系数恰好缩减为0, 这个特性可以帮助我们更好地理解数据。我们可以通过几何解释看到LASSO与岭回归之间的不同。
1. 岭回归和lasso的几何意义
以两个变量为例,残差平方和可以保湿为w1,w2的一个二次函数,是一个在三维空间中的抛物面,可以用等值线来表示。
岭回归的几何解释
岭回归的限制条件w12 + w22 ≤ λ,相当于在二维平面的一个圆。这个时候等值线与圆相切的点便是在约束条件下的嘴有点,如下图所示:

lasso的几何解释
标准线性回归的损失函数还是可以用二维平面的等值线表示,而约束条件则与岭回归的圆不同,LASSO的约束条件可以用菱形表示,如下图:

相比圆,菱形的顶点更容易与抛物面相交,顶点就意味着对应的很多系数为0,而岭回归中的圆上的任意一点都很同意与抛物面相交很难得到正好等于0的系数。这也就意味着,lasso、起到了很好的筛选变量的作用。
但是因为lasso的约束条件是绝对值形式,所以极大地增加了计算复杂度。这里我们使用sklearn调库来简单了解lasso最后返回的结果。
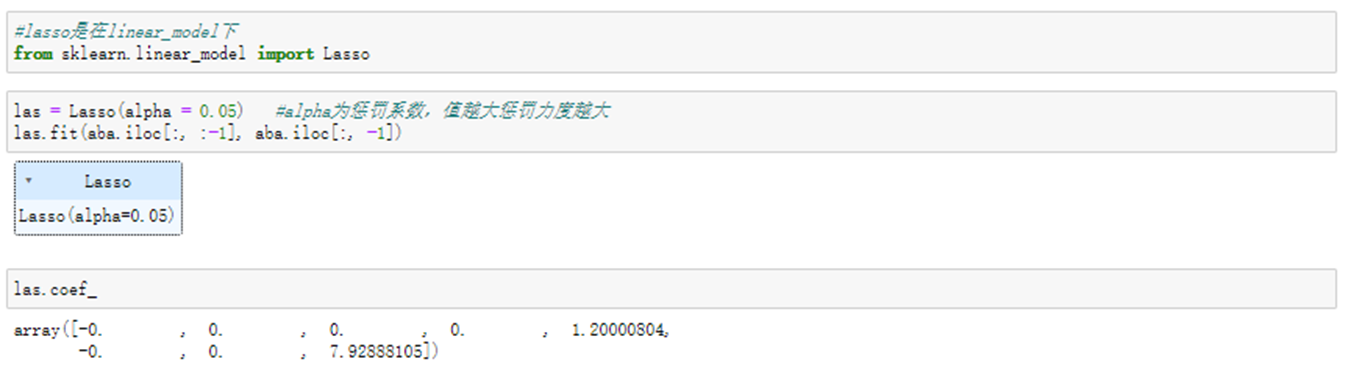
七、向前逐步回归
向前逐步回归算法可以得到与lasso差不多的效果,但是更加简单。它属于一种贪心算法,即每一步都尽可能减少误差。一开始所有的权重都设置为1,然后每一步所做的决策是对某个权重增加或者减少一个很小的值。
该算法伪代码如下:
数据标准化,使其分布满足均值为0,方差为1
在每轮迭代中:
设置当前最小误差lowestError为正无穷
对每个特征:
按步长增大或者缩小:
改变一个系数得到一个新的W
计算新W下的误差
如果误差Error小于lowestError:将当前w设置为Wbest
将W设置为新的Wbest
1. 构建辅助函数
数据标准化,使其分布满足均值为0,方差为1.
def regularize(xMat,yMat): """ 函数功能:数据标准化 """ inxMat = xMat.copy() #数据拷贝 inyMat = yMat.copy() yMean = yMat.mean(0) #行与行操作,求均值 inyMat = inyMat - yMean #数据减去均值 xMeans = inxMat.mean(0) #行与行操作,求均值 xVar = inxMat.var(0) #行与行操作,求方差 inxMat = (inxMat - xMeans) / xVar #数据减去均值除以方差实现标准化 return inxMat, inyMat
计算SSE
def rssError(yMat, yHat): sse = ((yMat.A-yHat.A)**2).sum() return sse
2. 向前逐步线性回归
def stageWise(dataSet, eps = 0.01, numIt = 100): """ 函数说明:前向逐步线性回归 参数说明: dataSet:原始数据集 eps:每次迭代需要调整的步长 numIt:迭代次数 返回: wsMat:numIt次迭代的回归系数矩阵 """ xMat0,yMat0 = get_Mat(dataSet) xMat,yMat = regularize(xMat0, yMat0) #数据标准化 m, n = xMat.shape wsMat = np.zeros((numIt, n)) #初始化numIt次迭代的回归系数矩阵 ws = np.zeros((n, 1)) #初始化回归系数矩阵 wsTest = ws.copy() wsMax = ws.copy() for i in range(numIt): #迭代numIt次 # print(ws.T) #打印当前回归系数矩阵 lowestError = np.inf #正无穷 for j in range(n): #遍历每个特征的回归系数 for sign in [-1, 1]: wsTest = ws.copy() wsTest[j] += eps * sign #微调回归系数 yHat = xMat * wsTest #计算预测值 sse = rssError(yMat, yHat) #计算平方误差 if sse < lowestError: #如果误差更小,则更新当前的最佳回归系数 lowestError = sse wsMax = wsTest ws = wsMax.copy() wsMat[i,:] = ws.T #记录numIt次迭代的回归系数矩阵 return wsMat
步长设置为0.01, 循环200次查看结果:

从结果中看出,w1始终为0,说明它不对目标值造成任何影响,也就是说这个特征可能是不需要的。另外,从结果中可以看到,第一个权重值在0.04~0.05之间震荡,可能是步长太长了。
再次尝试用更小的补偿和更多的迭代次数

与最小二乘法进行比较
这里对最小二乘法的回归系数计算函数做简单修改,增加数据标准化这一步。
def standRegres0(dataSet): xMat0,yMat0 =get_Mat(dataSet) xMat,yMat = regularize(xMat0, yMat0) #增加标准化这一步 xTx = xMat.T*xMat if np.linalg.det(xTx)==0: print('矩阵为奇异矩阵,无法求逆') return ws=xTx.I*(xMat.T*yMat) yHat = xMat*ws return ws

从结果可以看到,在500次迭代之后向前逐步线性回归的结果与常规最小二乘法的效果相似。
绘制结果图:

逐步线性回归算法的优点在于它可以帮助人们理解有的模型并做出改进。当构建了一个模型后,可以运行该算法找出重要的特征,这样就有可能及时停止对那些不重要特征的收集。
八、案例:预测乐高玩具套装的价格
乐高(LEGO)公司生产拼装类玩具,由很多大小不同的塑料插块组成。一般来说,这些插块都是成套出售,它们可以拼装成很多不同的东西,如船、城堡、一些著名建筑等。乐高公司每个套装包含的部件数据从10件到5000件不等。乐高示意图如下所示:

一种雷高套件基本上在几年后就会停产,但乐高的收藏者之间仍会在停产后彼此交易。所以这里我们使用回归方法对收藏者之间的交易价格进行预测。
1. 获取数据
因是同html网页文件中获取数据,故会使用到爬虫。
from bs4 import BeautifulSoup def scrapePage(data, infile, yr, numPce, origPrc): """ 函数功能:抓取一个网页的信息 参数说明: data:用来盛放抓取的所有信息 infile:html文件名 yr:年份 numPce:部件数目 origPrc:出厂价格 """ HTML_DOC = open(infile,encoding = 'utf-8').read() soup = BeautifulSoup(HTML_DOC,'lxml') i=1 #根据HTML页面结构进行解析 currentRow = soup.find_all('table', r = f'{i}') while(len(currentRow) != 0): currentRow = soup.find_all('table', r = f'{i}') title = currentRow[0].find_all('a')[1].text lwrTitle = title.lower() #查找是否有全新标签 if (lwrTitle.find('new') > -1): newFlag = 1 else:newFlag = 0 #查找是否已经标志出售,我们只收集已出售的数据 soldbutt = currentRow[0].find_all('td')[3].find_all('span') if len(soldbutt) == 0: print(f"商品 #{i} 没有出售") else: #解析页面获取当前价格 soldPrice = currentRow[0].find_all('td')[4] priceStr = soldPrice.text priceStr = priceStr.replace('$','') priceStr = priceStr.replace(',','') if len(soldPrice) > 1: priceStr = priceStr.replace('Free shipping', '') sellingPrice = float(priceStr) #去掉不完整的套装价格 if sellingPrice > origPrc * 0.5: data.append([yr, numPce, newFlag, origPrc,sellingPrice]) i+=1 currentRow = soup.find_all('table', r = f'{i}') def setDataCollect(data): scrapePage(data, 'lego/lego8288.html', 2006, 800, 49.99) scrapePage(data, 'lego/lego10030.html', 2002, 3096, 269.99) scrapePage(data, 'lego/lego10179.html', 2007, 5195, 499.99) scrapePage(data, 'lego/lego10181.html', 2007, 3428, 199.99) scrapePage(data, 'lego/lego10189.html', 2008, 5922, 299.99) scrapePage(data, 'lego/lego10196.html', 2009, 3263, 249.99)
2. 建立模型

在第0列增加常数项特征X0=1

用简单线性回归计算回归系数

计算模型预测效果

从散点图中可以看出,模型将价格分段预测,看起来效果还不错。
所以我们最后得到的模型就是:
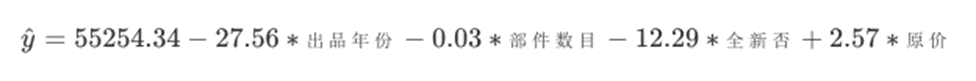
虽然说我们这个模型效果还不错,但是从实际意义上将,模型的解释性不是很好。从公式中看,魔心归队“出品年份”、“部件数据”和“全新否”这三个特征进行了惩罚,出品年份还比较好解释:年份越大说明距现在时间越短,二手成交价就会有所降低,但是部件数目和是否全新这两个特征就不太好解释了,部件数越多二手成交反而越低?全新的套装成交价反而越低?
再来看看我们的相关系数R2:

用sklearn中的树回归跑一遍,看看效果如何:






