算法系列之图--探查环

　　DFS可以被用来探查图中环的存在。仅有当一个图中存在‘回边’（back edge）时可以判定图中存在环。’回边‘是一条边，该边从一个结点到该结点或者到达该结点在DFS中的祖先。

　　下图有三条‘回边’，也就有三个环

　　

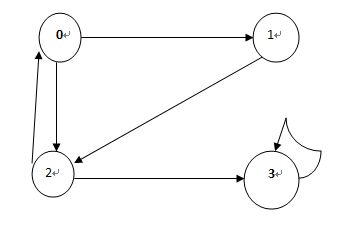
代码例子：

 1 #include <iostream>
 2 #include <limits.h>
 3 #include <list>
 4 using namespace std;
 5 
 6 class Graph{
 7     int v;//结点数
 8     list<int> *adj;//邻接表
 9     bool isCyclicUtil(int v,bool visited[],bool *stack);
10 public:
11     Graph(int v);
12     void addEdge(int u,int v);
13     bool isCyclic();
14 };
15 
16 Graph::Graph(int v){
17     this->v = v;
18     this->adj = new list<int>[v];
19 }
20 
21 void Graph::addEdge(int u,int v){
22     adj[u].push_back(v);
23 }
24 
25 bool Graph::isCyclicUtil(int v,bool visited[],bool resStack[]){
26     if (visited[v] == false){
27         cout<<v<<" ";
28         visited[v] = true;
29         resStack[v] = true;
30         list<int>::iterator iter = adj[v].begin();
31         for (;iter != adj[v].end();iter++){
32             if (!visited[*iter] && isCyclicUtil(*iter,visited,resStack))
33                 return true;
34             else if (resStack[*iter])
35                 return true;
36         }
37     }
38     resStack[v] = false;
39     return false;
40 }
41 
42 bool Graph::isCyclic(){
43     bool *visited = new bool[v];
44     bool *resStack = new bool[v];
45     for (int i=0;i<v;i++){
46         visited[i] = false;
47         resStack[i] = false;
48     }
49     for (int i=0;i<v;i++)
50         if (isCyclicUtil(i,visited,resStack))
51             return true;
52     return false;
53 }
54 
55 int main()
56 {
57     Graph g = Graph(4);
58     g.addEdge(2,0);
59     g.addEdge(2,3);
60     g.addEdge(0,1);
61     g.addEdge(0,2);
62     g.addEdge(3,3);
63     g.addEdge(1,2);
64 
65     if (g.isCyclic())
66         cout<<"Graph has a cycle"<<endl;
67     else
68         cout<<"Graph has no cycle"<<endl;
69 
70     return 0;
71 }

 

运行结果为：

 

 

代码参考：http://www.geeksforgeeks.org/detect-cycle-in-a-graph/

posted on 2015-03-18 10:21  lxiao_socool  阅读(175)  评论(0)  编辑  收藏  举报

导航