抽象语法树(AST)
1.简介
抽象语法树（abstract syntax code，AST）是源代码的抽象语法结构的树状表示，树上的每个节点都表示源代码中的一种结构，这所以说是抽象的，是因为抽象语法树并不会表示出真实语法出现的每一个细节，比如说，嵌套括号被隐含在树的结构中，并没有以节点的形式呈现。抽象语法树并不依赖于源语言的语法，也就是说语法分析阶段所采用的上下文无文文法，因为在写文法时，经常会对文法进行等价的转换（消除左递归，回溯，二义性等），这样会给文法分析引入一些多余的成分，对后续阶段造成不利影响，甚至会使合个阶段变得混乱。因些，很多编译器经常要独立地构造语法分析树，为前端，后端建立一个清晰的接口。
百度百科版本：
在计算机科学中，抽象语法树（Abstract Syntax Tree，AST），或简称语法树（Syntax tree），是源代码语法结构的一种抽象表示。它以树状的形式表现编程语言的语法结构，树上的每个节点都表示源代码中的一种结构。
之所以说语法是“抽象”的，是因为这里的语法并不会表示出真实语法中出现的每个细节。比如，嵌套括号被隐含在树的结构中，并没有以节点的形式呈现；而类似于if-condition-then这样的条件跳转语句，可以使用带有两个分支的节点来表示。和抽象语法树相对的是具体语法树（通常称作分析树）。一般的，在源代码的翻译和编译过程中，语法分析器创建出分析树。一旦AST被创建出来，在后续的处理过程中，比如语义分析阶段，会添加一些信息。
2.实例
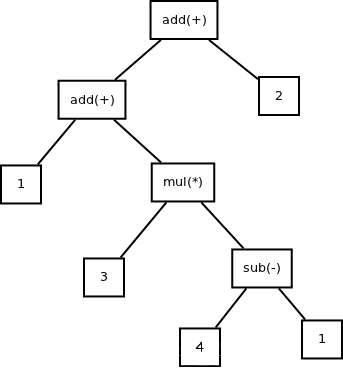
- 四则运算表达式：1+3*(4-1)+2
其抽象语法树为：
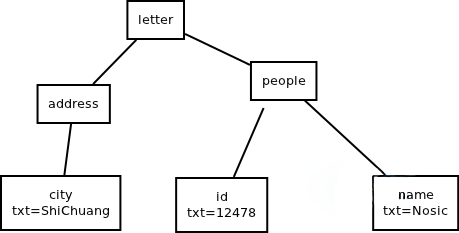
- 代码1：
<letter>
<address>
<city>ShiChuang</city>
</address>
<people>
<id>12478</id>
<name>Nosic</name>
</people>
</letter>
其抽象语法树为：
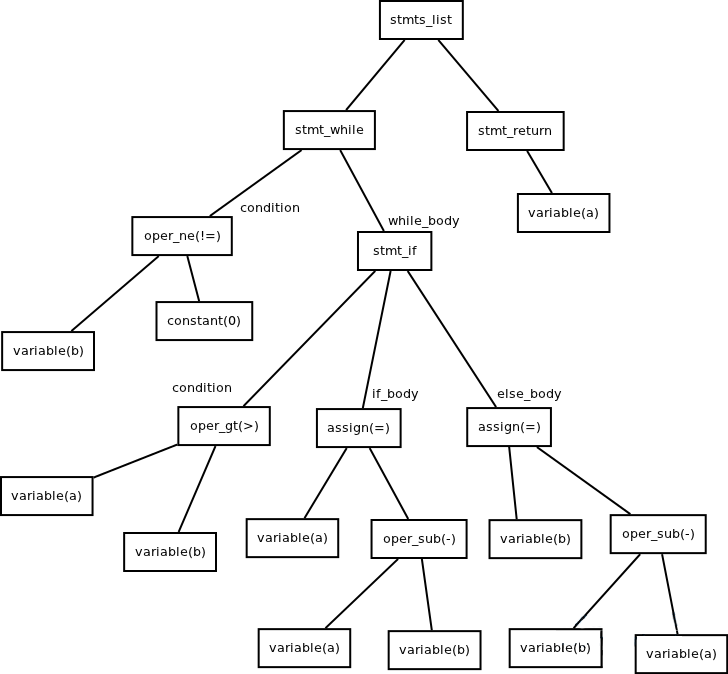
- 代码2：
while b != 0
{
if a > b
a = a-b
else
b = b-a
}
return a
其抽象语法树为：
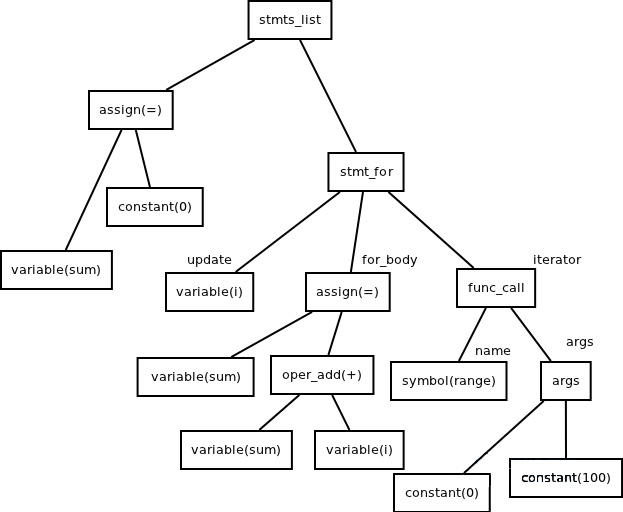
- 代码3：
sum=0
for i in range(0,100)
sum=sum+i
end
其抽象语法树为：
3.为什么需要抽象语法树
当在源程序语法分析工作时，是在相应程序设计语言的语法规则指导下进行的。语法规则描述了该语言的各种语法成分的组成结构，通常可以用所谓的前后文无关文法或与之等价的Backus-Naur范式(BNF)将一个程序设计语言的语法规则确切的描述出来。前后文无关文法有分为这么几类：LL(1)，LR(0)，LR(1)， LR(k) ,LALR(1)等。每一种文法都有不同的要求，如LL(1)要求文法无二义性和不存在左递归。当把一个文法改为LL(1)文法时，需要引入一些隔外的文法符号与产生式。
例如，四则运算表达式的文法为：
文法1.1：
E->T|EAT T->F|TMF F->(E)|i A->+|- M->*|/
改为LL(1)后为：
E->TE' E'->ATE'|e_symbol T->FT' T'->MFT'|e_symbol F->(E)|i A->+|- M->*|/
例如，当在开发语言时，可能在开始的时候，选择LL(1)文法来描述语言的语法规则，编译器前端生成LL(1)语法树，编译器后端对LL(1)语法树进行处理，生成字节码或者是汇编代码。但是随着工程的开发，在语言中加入了更多的特性，用LL(1)文法描述时，感觉限制很大，并且编写文法时很吃力，所以这个时候决定采用LR(1)文法来描述语言的语法规则，把编译器前端改生成LR(1)语法树，但在这个时候，你会发现很糟糕，因为以前编译器后端是对LL(1)语树进行处理，不得不同时也修改后端的代码。
抽象语法树的第一个特点为:不依赖于具体的文法。无论是LL(1)文法，还是LR(1)，或者还是其它的方法，都要求在语法分析时候，构造出相同的语法树，这样可以给编译器后端提供了清晰，统一的接口。即使是前端采用了不同的文法，都只需要改变前端代码，而不用连累到后端。既减少了工作量，也提高的编译器的可维护性。
抽象语法树的第二个特点为:不依赖于语言的细节。在编译器家族中，大名鼎鼎的gcc算得上是一个老大哥了，它可以编译多种语言，例如c，c＋＋，java，ADA，Object C， FORTRAN， PASCAL， COBOL等等。在前端gcc对不同的语言进行词法，语法分析和语义分析后，产生抽象语法树形成中间代码作为输出，供后端处理。要做到这一点，就必须在构造语法树时，不依赖于语言的细节，例如在不同的语言中，类似于if－condition－then这样的语句有不同的表示方法
在c中为：
if(condition)
{
do_something();
}
在fortran中为：
If condition then
do_somthing()
end if
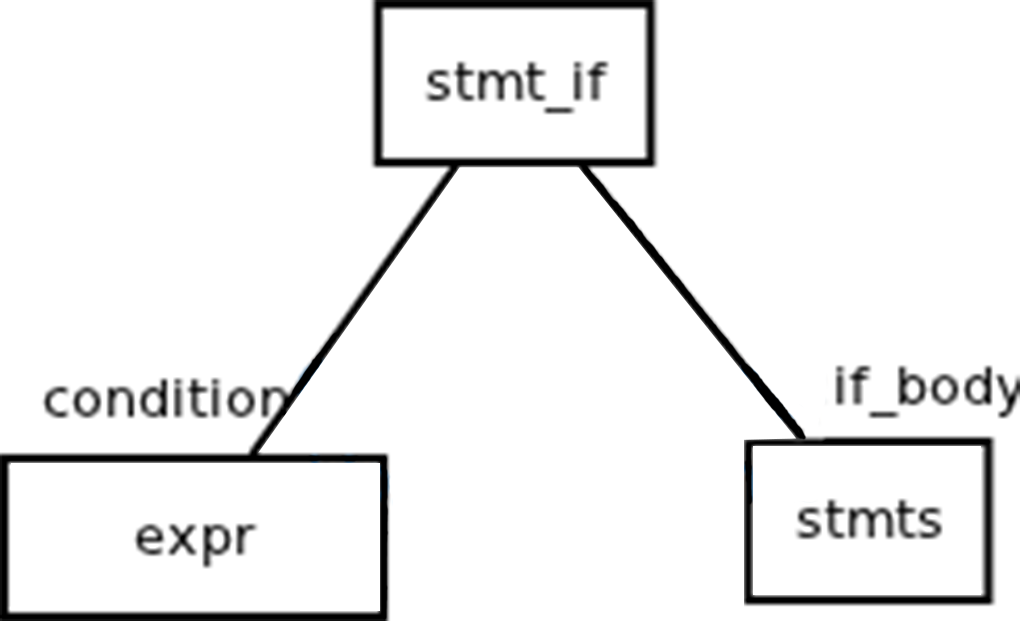
在构造if－condition－then语句的抽象语法树时，只需要用两个分支节点来表于，一个为condition，一个为if_body。如下图：
在源程序中出现的括号，或者是关键字，都会被丢掉。
我的公众号！
把你的手放在滚热的炉子上一分钟，感觉起来像一小时。坐在一个漂亮姑娘身边整整一小时，感觉起来像一分钟。这就是相对论。
——爱因斯坦
