关于SVD-LLM的应用-基于SVD量化

关于SVD-LLM的应用-基于SVD量化

一 背景

　　论文连接：https://arxiv.org/pdf/2403.07378 这是论文

　　github：https://github.com/AIoT-MLSys-Lab/SVD-LLM

 

二 什么是SVD

 　　SVD可能是 可以把矩阵向量 转化到另外一个 空间角度，以方便数据处理。

　　2.1 概念

　　SVD（Singular Value Decomposition，奇异值分解）是一种矩阵分解的技术，它可以将一个矩阵分解成三个矩阵的乘积。给定一个m×n的矩阵A，SVD 将其分解为以下形式：

　　A = U * Σ * V^T

　　其中U 是一个m×m的正交矩阵，Σ 是一个m×n的对角矩阵，V^T（V 的转置）是一个n×n的正交矩阵。

　　对角矩阵

　　对角矩阵是一种特殊的方阵，其除了对角线上的元素外，其余元素均为零。

　　正交矩阵

　　正交矩阵是指其行向量和列向量是正交的方阵。在数学上，一个n×n的矩阵A如果满足以下条件，则称为正交矩阵：

1. A 的每一列都是单位向量（向量的长度为1）；
2. A 的每一列两两正交（即任意两列的内积为0，表示它们垂直）；
3. A 的每一行也是单位向量且两两正交

　　正交变换

         

 

          

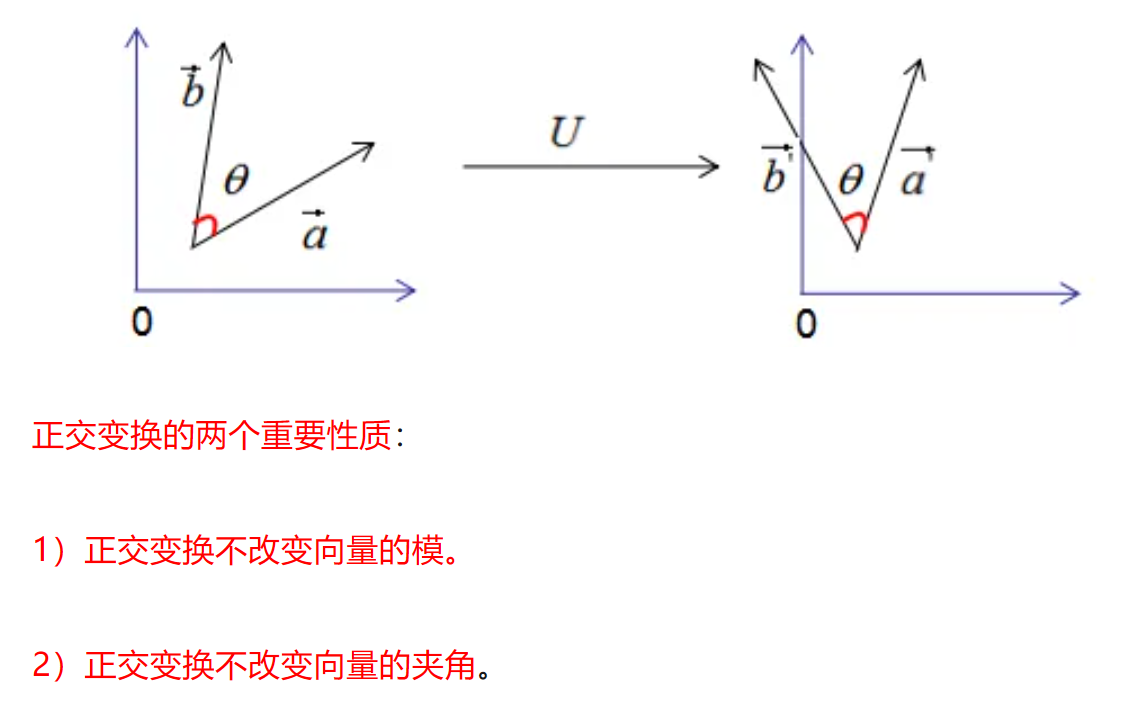
　　向量长度

　　||v|| = sqrt(x1^2 + x2^2 + ... + xn^2)，将每个分量的平方求和后再开根号。这样计算出的结果就是向量的长度或模。

 

三 SVD-LLM原理

 　　示意图：

       

　　Key Designs

• Truncation-Aware Data Whitening: Ensure truncating smaller singular values has lower compression loss.
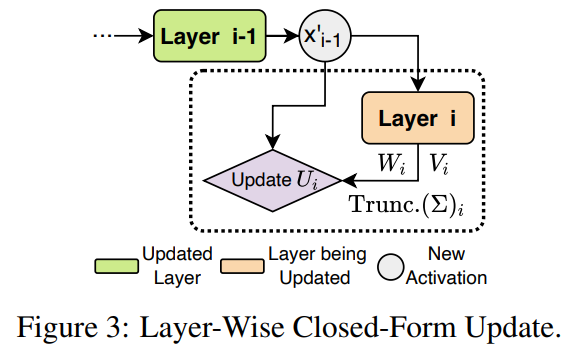
• Layer-Wise Closed-Form Update: Compensate for accuracy degradation under high compression ratio.

　　更详细的原理  来自论文

         

 

　　

              

 

　　为什么使用SVD呢？ 

　　U和V 是正交矩阵，epsilon矩阵 是对角矩阵，  =>  这些矩阵都 容易量化吗？

 

 

四 怎么使用SVD-LLM

　　已封装好脚本 主要对LLAMA-7B 可以使用