机器学习基础功能练习II
机器学习基础功能练习II
一、导入sklearn 数据集
from sklearn.datasets import load_diabetes diabetes = load_diabetes() """返回字典,数据集的descr,data,feature_names等关键数据 diabetes.data 是一个矩阵 sklearn.datasets.load_boston sklearn.datasets.load_breast_cancer sklearn.datasets.load_diabetes sklearn.datasets.load_digits sklearn.datasets.load_files sklearn.datasets.load_iris """ print(diabetes) print(diabetes.feature_names) print(diabetes.data)
X = diabetes.data
y = diabetes.target
二、分隔数据集
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) test_size=0.3 代表7:3,random_state=1 0~42
三、模型训练与预测
from sklearn.linear_model import LinearRegression
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
四、绘制结果图
plt.figure()
plt.plot(range(len(y_predict)), y_predict, 'b', label="predict")
plt.plot(range(len(y_predict)), y_test, 'r', label="test")
plt.legend(loc="upper right") # 显示图中的标签
plt.xlabel("the x")
plt.ylabel('value')
plt.show()
五、线性回归的指标
from sklearn.metrics import explained_variance_score, \
mean_absolute_error, \
mean_squared_error, \
median_absolute_error, r2_score
# 由于回归分析的目标值是连续值,因此我们不能用准确率之类的评估标准来衡量模型的好坏,
# 而应该比较预测值(Predict)和实际值(Actual)之间的差异程度。
# 其中,均方根误差(root-mean-square error,简称 RMSE)是最常见的评估标准之一。
print('数据线性回归模型测试集的平均绝对误差为:',mean_absolute_error(y_test, y_predict))
print('数据线性回归模型测试集的均方误差为:',mean_squared_error(y_test, y_predict))
print('数据线性回归模型测试集的中值绝对误差为:',median_absolute_error(y_test, y_predict))
print('数据线性回归模型测试集的可解释方差值为:',explained_variance_score(y_test, y_predict))
print('数据线性回归模型测试集的R方值为:',r2_score(y_test, y_predict))
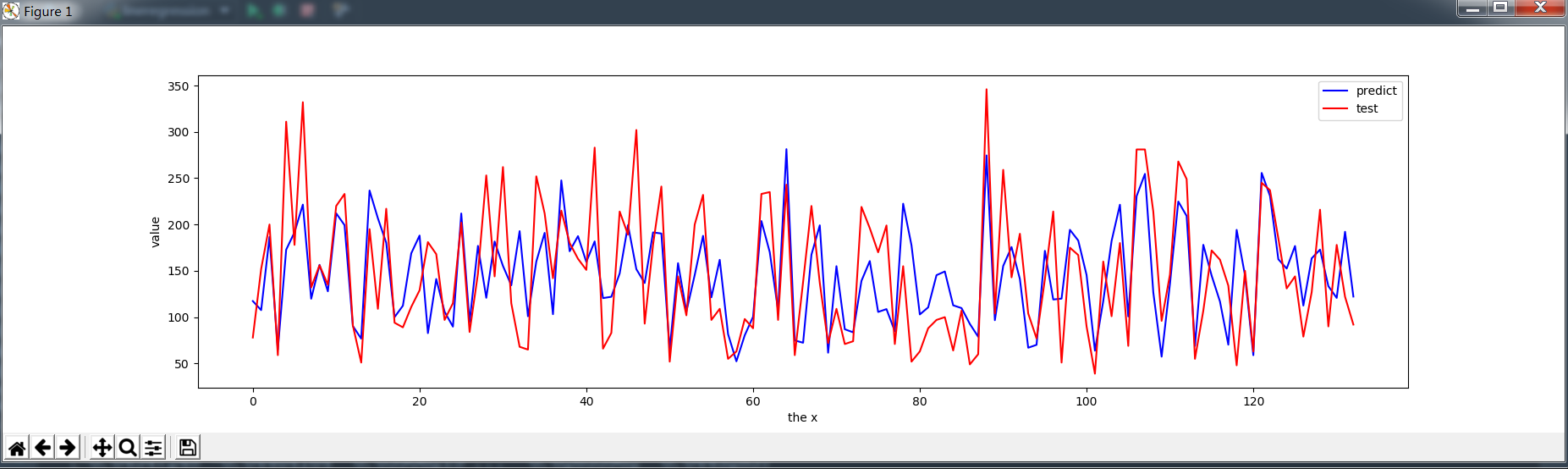
效果不是很好
数据线性回归模型测试集的平均绝对误差为: 41.64925030150086
数据线性回归模型测试集的均方误差为: 2827.0709606368036
数据线性回归模型测试集的中值绝对误差为: 35.94007730856664
数据线性回归模型测试集的可解释方差值为: 0.4395412676763393
数据线性回归模型测试集的R方值为: 0.4384569849129575
欠拟合的原因在于: 不是对比测试集和训练集的mse,而是mse在两个数据集都很高。
六、加入决策树
from sklearn.tree import DecisionTreeRegressor dtr = DecisionTreeRegressor(criterion="mse", splitter="best",max_depth=3) dtr.fit(X_train,y_train) y_pred = dtr.predict(X_test)
max_depth对结果有很大影响
第二部需要从数据研究开始 >>>>>>
对比线性回归
plt.plot(range(len(y_pred)),y_pred,"g",label="dtr_pred")
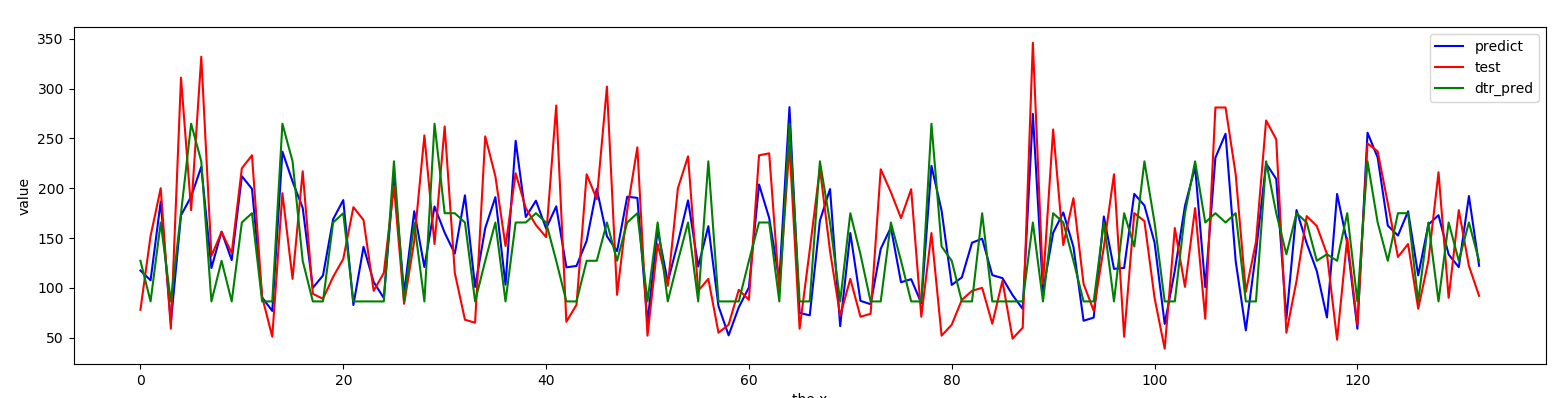
七、交叉验证方法优化模型
交叉验证的结果是衡量模型性能指标的一种方法。是一种评价方法。
1 交叉验证有效防止过拟合
防止过拟合就能在测试集上有好效果
崔卿解答:“交叉验证怎么避免过拟合呢” 以我的理解,交叉验证并不能避免过拟合,避免过拟合还是有其他很多算法层面的方式,交叉验证主要还是效果调优用
理解:不能防止过拟合,只是评价标准
2 那么交叉验证怎么避免过拟合呢?
如使用5折交叉验证,那么测试结果为5个score,也分别对应5个模型,选择score中的中位数对应的那个模型吗?
阿里 崔卿 解答:这个一般选最好的,但不一定就是最好的,验证集/测试集只是评估模型效果的一种方式 问题
理解:比如3折交叉验证,[0.98,0.99,1.00],实际应用中能说明,score在0.99左右,模型堪用。然后选取三号模型。进一步会在业务中评估。
3 在数据集a训练一个模型后,再放入另一组数据集b训练。
那么模型相当于在a+b的测试合集上训练出来的还是仅仅是在 数据集b上训练出来的呢?
sklearn代码如下,如果只是针对sklearn代码来说model是不是只用最后一次fit的训练参数。
model=LogisticRegression()
model.fit(Xa,ya)
# 此时再放入Xb,yb中训练
model.fit(Xb,yb)
阿里 崔卿 解答:2, 会重头训练 https://stackoverflow.com/questions/49841324/what-does-calling-fit-multiple-times-on-the-same-model-do
理解:重新刷新。可以增量训练partial_fit
4 在5折交叉验证得到5个模型,5组模型参数(W权重),取均值作为模型的最终权重是否可以防止过拟合?
如果不可行的话,是什么道理呢?
如果可行的话,sklearn代码需要调用哪个api呢?
阿里 崔卿 解答:线性模型取均值是可行的,某种程度也可以避免过拟合,但这种方法不常用,如果其中一个模型过拟合很厉害,参数值非常大,则会导致结果依然过拟合或者异常。可以用LinearRegression的attributes coef_来获取参数 https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
理解:可行但是保证model中不能有很大过拟合,否则结果还是过拟合。LinearRegression的attributes coef_可修改。
model.coef_ = np.array([0 for x in range(10)])
model.coef_ 返回一个 class numpy.ndarray





