机器学习-聚类

聚类：
(一)聚类的基本概念
(二)原型聚类
(三)密度聚类
(四)层次聚类
(五)本章小结

(零)前置知识

0 基本概念

0.1 P，NP，NPC和NPhard问题

0.1.1. P问题

P问题(easy to find): 能在多项式时间内解决的问题
考虑时间复杂度，P问题的时间复杂度总是可以用多项式表示，或小于某多项式表示的。
例如计算1-1000的连续整数之和：这个问题就比较简单，无论是编程还是使用高斯求和公式都可以在有限可接受的时间内完成，这种算是P类问题。
冒泡排序算法，时间复杂度为$O(n^2)$，显然是多项式时间内可以解决的问题。
更快的排序算法如快速排序，时间复杂度为$O(nln(n))$，也是多项式时间内可以解决的问题。

0.1.2. NP问题

NP问题(easy to check): 不能在多项式时间内解决或不确定能不能在多项式时间内解决，但能在多项式时间验证的问题。
为什么是”不能或不确定能不能“呢，因为关于P是否等于NP，人类尚且没有统一的答案。但是人们现在普遍认为P不等于NP。
典型的NP问题如哈密顿回路问题：

天文学家哈密顿(William Rowan Hamilton) 提出，在一个有多个城市的地图网络中，寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径。

可以证明，哈密顿回路问题是一个NP问题，人们往往要通过穷举这样笨拙的方法寻找问题的解，然而，显然我们可以在多项式时间内判断一个既定的解是否是正确的。

又例如计算地球上所有原子个数之和：这个问题就很困难甚至无解，但是现在有个答案是300个，显然是错的，所以很容易验证但不容易求解，这种算NP类问题。

0.1.3 NPC问题

NPC问题：它是一个NP问题，且所有的NP问题都可以用多项式时间约化到它。更本质的理解，我们把规约看作一种偏序关系，那么NPC就是NP的上届。一句话，所有NP问题都不比NPC难。

首先解释一下规约的概念，如果能找到这样一个变化法则，对任意一个程序A的输入，都能按这个法则变换成程序B的输入，使两程序的输出相同，那么我们说，问题A可约化为问题B，即可以用问题B的解法解决问题A，或者说，问题A可以“变成”问题B。

例如A是求一元一次方程的解，B是求一元二次方程的解，A的输入参数是k和m，B的输入参数是a，b和c。
显然，我们可以令 $a=k^2,b=2km,c=m^2$ ，这样我们就可以通过解问题B来求解问题A了。当然，A和B问题都不是NP问题。
可以看出，B的时间复杂度高于或者等于A的时间复杂度。也就是说，问题A不比问题B难。

显然，NPC问题是NP问题的一部分，如果P=NP成立，P，NP和NPC将重合在一起。

0.1.4 NPhard问题
NPHard问题：NPhard满足所有的NP问题都可以用多项式时间约化到它，但并不要求其是一个NP的问题。或者说，NPhard是所有问题的上界。也就是说，所有问题都不比NPhard难。
可以看出，NPhard问题的范围比NPC的范围更大。

0.2 可计算问题与不可计算问题

0.2.1 可计算问题

可计算问题的边界是什么？
　　可以说，可计算问题包括了P，NP和NPC，但不限于NP问题。由NP的定义可以看出，NP的问题的解必须是在多项式时间内可以验证的，而显然存在这样的问题，即问题的解既不能在多项式时间内找到，也不能在多项式时间内验证。

　　理论上说，可计算问题的数目和自然数集的数目相当，可以用如下方法证明：任何可计算问题都可以被图灵机计算，图灵机的算法和数据由纸带给出，而纸带则是由0和1组成的序列，因此，所有可计算问题都可以和一个由0和1组成的序列对应。而0和1组成的序列可以被看做二进制数，二进制数和十进制数一一对应，因此可计算问题和自然数集等势。

0.2.2.不可计算问题

　　定义了可计算问题后，我们很自然的像尝试计数不可计算问题。但遗憾的是，不可计算问题是不可数的，它的势远大于可计算问题。

什么样的问题是不可计算的？
　　一个典型的例子是，消除机器学习中过拟合的问题是不可计算问题，因为对于任意的学习问题，样本的特征空间是无穷的，同时我们无法得到样本的分布。回到之前图灵机的例子，我们没有办法把所有的输入都写在纸上，因为它是无穷的，所以我们没有办法彻底解决过拟合的问题。

0.2.3. 机器学习所解决的问题

　　想找到一个问题的贝叶斯最有决策器是NPhard的，因此我们往往需要通过设置阈值等方式使学习算法在合适的时间停止，从而得到问题的近似解。同时，过拟合的出现是不可避免的，彻底解决过拟合是NPhard的。

(一)聚类的基本概念

1.1 聚类任务

　　在“无监督学习”(unsupervised learning)中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。此类学习任务中研究最多、应用最广的“聚类”(clustering)。

　　聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”(cluster)。通过这样的划分，每个簇可能对应与一些潜在的概念(类别)，如在西瓜数据集中划分为“浅色瓜”，“深色瓜”，“有籽瓜”，“无籽瓜”，甚至“本地瓜”，“外地瓜”等；

　　需要说明的是，这些概念对聚类算法而言事先是未知的，聚类过程仅能自动形成簇结构，簇所对应的概念语义需由使用者来把握和命名。

　　形式化地说，假定样本集$D=\left\{x_1,x_2,...,x_m\right\}$包含m个无标记样本，每个样本$x_i = {x_{i1};x_{i2};...;x_{in}}$是一个n维特征向量，则聚类算法将样本$D$划分为k个不相交的簇${C_l|l=1,2,...,k}$，其中$C_{l'}\cap_{l'\neq l}C_l=\varnothing$且$D=\cup_{l=1}^k C_l$。相应地，我们用$\lambda_j∈ \left\{1,2,...,k\right\}$表示样本$x_j$的“簇标记”(cluster label)，即$x_j∈C_{\lambda_j}$。于是，聚类的结果可用包含$m$个元素的簇标记向量$\lambda=(\lambda_1; \lambda_2;...;\lambda_m)$表示。
　　
　　聚类既能作为一个单独的过程，用于找寻数据内在的分布结果，也可作为分类等其他学习任务的前驱过程。例如，在一些商业应用中需对新用户的类型进行判别，但定义“用户类型”对商家来说却可能不太容易，此时往往可先对用户数据进行聚类，根据聚类结果将每个簇定义为一个类，然后再基于这些类训练分类模型，用于判别新用户的类型。

　　基于不同的学习策略，人们设计出多种类型的聚类算法。为了更好的选用和讨论不同聚类算法类型的优劣，我们先来讨论聚类算法设计的两个基本问题——性能度量和距离计算。

1.2 性能度量

　　聚类性能度量，亦称聚类“有效性指标”(validity index)。
与监督学习中的性能度量作用相似，对聚类结果，我们需通过某种性能度量来评估其好坏；另一方面，若明确了最终将要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。

　　聚类是将样本集D划分为若干互不相交的子集，即样本簇。那么，什么样的聚类结果比较好呢？
直观上看，我们希望“物以类聚”，即同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。
换言之，聚类结果的“簇内相似度”(intra-cluster similarity)高且“簇间相似度”(inter-cluster similarity)低。

　　聚类性能度量大致有两类指标作为标准。

外部指标，是将聚类结果与某些“参考模型”进行比较。
内部指标，是直接考察聚类结果而不利用任何参考模型。

1.2.1 外部指标

　　对数据集$D={x_1,x_2,...,x_m}$，假定通过聚类给出的簇划分为$\mathcal{C}=\left\{C_1,C_2,...,C_k\right\}$，参考模型给出的簇划分为$\mathcal{C}^* = \left\{C_1^*,C_2^*,...,C_s^* \right\}$.相应地，令$\lambda$与$\lambda^*$分别表示与$\mathcal{C}$和$\mathcal{C}^*$对应的簇标记向量。

　　由此聚类结果为$\lambda$，参考模型结果是$\lambda^*$，我们将样本两两配对考虑，定义

\[a =|SS|，\quad SS= \left\{(x_i,x_j)|\lambda_i=\lambda_j, \lambda_i^*=\lambda_j^*, i<j \right\}, 参考结果同类簇，聚类结果同类簇 \\ b =|SD|，\quad SS= \left\{(x_i,x_j)|\lambda_i=\lambda_j, \lambda_i^* \neq \lambda_j^*, i<j \right\}, 参考结果不同类簇，聚类结果同类簇 \\ c =|DS|，\quad SS= \left\{(x_i,x_j)|\lambda_i \neq \lambda_j, \lambda_i^*=\lambda_j^*, i<j \right\} ,参考结果同类簇，聚类结果不同类簇\\ d =|DD|，\quad SS= \left\{(x_i,x_j)|\lambda_i \neq \lambda_j, \lambda_i^* \neq \lambda_j^*, i<j \right\},参考结果不同类簇，聚类结果不同类簇 \]

说明：
　　其中，对于聚类划分出的两个簇，$\mathcal{C}$与$\mathcal{C}^*$。
　　集合$SS$包含了在$\mathcal{C}$中隶属于相同簇且在$\mathcal{C}^*$中也隶属于相同簇的样本对，
　　集合$SD$包含了在$\mathcal{C}$中隶属于相同簇但在$\mathcal{C}^*$中隶属于不同簇的样本对，
　　集合$DS$包含了在$\mathcal{C}$中不隶属于相同簇但在$\mathcal{C}^*$中隶属于相同簇的样本对，
　　集合$DD$包含了在$\mathcal{C}$中不隶属于相同簇且在$\mathcal{C}^*$中也隶属于相同簇的样本对。
　　显然$a$和$b$代表着聚类结果好坏的正能量，$b$和$c$则表示参考结果和聚类结果相矛盾

基于上面的两个簇$\mathcal{C}$与$\mathcal{C}^*$的关系式，可导出以下这些常用的聚类性能度量外部指标。

Jaccard系数(Jaccard Coeffcient，简称JC)

\[JC = \frac{a}{a + b + c} \quad \quad (9.5) \]
FM指数(Fowlkes and Mallows Index，简称FML)

\[FMI = \sqrt{\frac{a}{a+b} \cdot \frac{a}{a+c}} \quad \quad (9.6) \]
Rand指数(Rand Index，简称RI)

\[RI = \frac{2(a+d)}{m(m-1)} \quad \quad (9.7) \]
显然，上述性能度量的结果值均在[0,1]区间，值越大越好。

式(9.7)的解释

将式(9.7)变形为$RI = \frac{a + d}{m(m_1)/2} = \frac{a + d}{a + b + c +d}$
因为RI肯定不大于1，之所以$a + b + c + d = m(m-1)/2$，这是因为式(9.1)$\sim$遍历了所有$(x_i, x_j)$组合对$(i \neq j)$：其中$i = 1$时$j$可以取2到$m$共$m-1$个值，$i=2$时$j$可以取$3$到$m$共$m-2$个值，...，$i = m-1$时$j$仅可以取$m$共1个值，因此$(x_i, x_j)$组合对的个数从$1$到$m-1$求和，根据等差数列求和公式即得$m(m-1)/2$。

1.2.2 内部指标

　　内部指标即不依赖任何外部模型，直接对聚类的结果进行评估，聚类的目的是想将那些相似的样本尽可能聚在一起，不相似的样本尽可能分开，直观来说：簇内高内聚紧紧抱团，簇间低耦合老死不相往来。

　　考虑聚类结果的簇划分$\mathcal{C} = \left\{C_1,C_2,...,C_k \right\}$，定义

\[\begin{align} & 平均距离　\quad avg(C) = \frac{2}{|C|(|C|-1)} \sum_{1\leq i\leq j \leq |C|} dist(x_i,x_j),\quad \quad (9.8)\\ & 最远距离 \quad diam(C) = max_{1\leq i\leq j \leq |C|} dist(x_i,x_j) \quad \quad (9.9)\\ & 最近邻距离　d_{min}(C_i,C_j) = min_{x_i∈C_i,x_j∈C_j}　dist(x_i,x_j), \quad \quad (9.10)\\ & 中心偏离距离　d_{cen}(C_i,C_j) = dist(\mu_i, \mu_j) \quad \quad (9.11) \end{align} \]

其中，$|C|$表示簇$C$中样本的个数，
　　　$dist(\cdot,\cdot)$用于计算两个样本之间的距离；
　　　$\mu$代表簇C的中心点$\mu=\frac{1}{|C|}\sum_{1\leq i \leq |C|}x_i$。
　　　显然，$avg(C)$对应于簇$C$内样本间的平均距离，
　　　$diam(C)$对应与簇$C$内样本间的最远距离，
　　　$d_{min}(C_i,C_j)$对应与簇$C_i$与$C_j$簇最近样本间的距离，
　　　$d_{cen}(C_i,C_j)$对应与簇$C_i$与$C_j$簇中心点间的距离

基于上列式子，可到处以下这些常用的聚类性能度量内部指标。

DB指数(Davies-Bouldin Index，简称DBI)
\[DBI = \frac{1}{k} \sum \limits_{i=1}^k \underset{j\neq i}{max} \left(\frac{avg(C_i)+avg(C_j)}{d_{cen}(C_i,C_j)} \right). \quad \quad (9.12) \]

式(9.12)的解释

式中，$k$表示聚类结果中簇的个数，因此该式的DB值越小越好，因为我们希望“物以类聚”，即同一簇的样本尽可能彼此相似，$avg(C_i)$和$avg(C_j)$越小越好；我们希望不同簇的样本尽可能不同，即$d_{cen}(C_i, C_j)$越大越好。

Dunn指数(Dunn Index，简称DI)
\[DI = \underset{1 \leq i \leq k}{min} \left\{\underset{j\neq i}{max} \left( \frac{d_{min}(C_i,C_j)}{\underset{1\le l \leq k}{max}　diam(C_l)}\right) \right\}. \quad \quad (9.13) \]

显然，DBI的值越小越好，而DI则相反，值越大越好。

1.3 距离计算

1.3.1 距离$dist(\cdot,\cdot)$的充分条件

对函数$dist(\cdot,\cdot)$，若它是一个“距离度量”(distance measure)，则需要满足一些基本性质：

非负性：$dist(x_i,x_j)\geq 0$ ; (9.14)
同一性：$dist(x_i,x_j)=0$当且仅当$x_i=x_j$; (9.15)
对称性：$dist(x_i,x_j)=dist(x_j,x_i)$; (9.16)
直递性：$dist(x_i,x_j) \leq dist(x_i,x_k) + dist(x_k,x_j)$. (9.17)

1.3.2 几种距离与属性

1.3.2.1 闵可夫斯基距离

　　给定样本$x_i=(x_{i1};x_{i2};...;x_{in})$与$x_j=(x_{j1};x_{j2};...;x_{jn})$，最常用的是“闵可夫斯基距离”(Minkowski distance)

\[dist_{mk}(x_i,x_j) = \left(\sum \limits_{u=1}^n |x_{iu}-x_{ju}|^p \right)^{\frac{1}{p}} \quad \quad (9.18) \]

对$p \geq 1$，上式显然满足“距离度量”的基本性质。

以下是针对$p$不同取值，得到的对应距离。

1.3.2.2 曼哈顿距离

当$p=1$时，闵可夫斯基距离即为曼哈顿距离(Manhattan distance)

\[dist_{man}(x_i,x_j) = ||x_i-x_j||_1 = \sum \limits_{u=1}^n |x_{iu} - x_{ju}|^2. \quad \quad (9.20) \]

1.3.2.3 欧氏距离

当$p=2$时，闵可夫斯基距离即为欧氏距离(Euclidean distance)

\[dist_{ed}(x_i,x_j) = ||x_i-x_j||_2 = \sqrt{\sum \limits_{u=1}^n |x_{iu} - x_{ju}|^2} \quad \quad (9.19) \]

1.3.2.4 欧氏距离和曼哈顿距离

当提及“距离”的概念，通常意味着从A到B的“最短”路径。
下图显示出了在二维平面上欧氏距离(黑色)和曼哈顿距离(蓝色)。

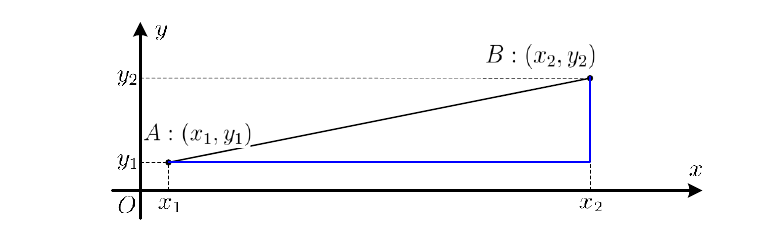
即从A到B的欧氏距离是两点之间的直线最短路径(空间任意位置均可作为路径)，而A到B的曼哈顿距离则是当只能沿着平行各坐标轴方向行走时的最短路径。

1.3.2.5 几种属性

我们常将属性划分为

“连续属性”(continuous attribute)，在定义域上有无穷多个可能的取值
对于连续值的属性，一般都可以被学习器所用，有时会根据具体的情形作相应的预处理，例如：归一化等；
“离散属性”(categorical attribute)，在定义域上是有限个取值
而对于离散值的属性，需要作下面进一步的处理：

若属性值之间存在序关系，则可以将其转化为连续值，例如：身高属性“高”“中等”“矮”，可转化为$\{1, 0.5, 0\}$。
若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“女”，可转化为$\{(1,0),(0,1)\}$。

然而，在讨论距离计算是，我们更加关心属性是否定义了“序”的关系，即为属性有序或无序

“有序属性”(ordinal attribute)，即样本的离散属性直接在属性值上计算距离。
例如，定义域为{1,2,3}的离散属性与连续属性更接近一些，样本元素“1”与“2”比加近(距离为1)，与“3”比较远(距离为2)。这样的属性称为“有序属性”。
“无序属性”(non-ordinal attribute)，不能直接在属性值上计算距离
例如，定义域为{飞机，火车，轮船}这样的离散属性则不能直接在属性值上计算距离，称为“无序属性”。
“混合属性”：由若干个有序属性与无序属性结合而成的属性集合。
例如定义域为{(飞机，1)，(火车，2)，(轮船，3)}这样的属性，包含连续属性、离散属性，且对于连续属性是有序，离散属性是无序的，称为“混合属性”

显然，闵可夫斯基距离可用于有序属性，无序属性和混合属性则需要其他方式计算距离。
此外，需要注意的是，这里的属性皆可理解为特征feature，特征也即为我们处理和计算距离的对象。

对于无序属性可采用VDM(Value Difference Metric)进行距离计算。
其中$i$表示类簇，令$m_{u,a}$表示属性$u$上取值为$a$的样本数，$m_{u,a,i}$表示在第$i$个样本簇中在属性$u$上取值为$a$的样本数，$k$为样本簇数，则属性$u$上两个离散值$a$与$b$之间的VDM距离为

\[VDM_p(a,b) = \sum \limits_{i=1}^k \left|\frac{m_{u,a,i}}{m_{u,a}} - \frac{m_{a,b,i}}{m_{u,b}} \right|^p . \quad \quad (9.21) \]

式(9.21)的解释

该式符号较为抽象，下面计算表4.1的西瓜数据集2.0属性根蒂上“蜷缩”和“稍蜷”两个离散值之间的距离。
此时，$u$为“根蒂”，$a$为属性根蒂上取值为“蜷缩”，$b$为属性根蒂上取值为"稍蜷"，根据边注，此时样本类别已知(好瓜/坏瓜)，因此$k=2$。
从表4.1中可知，根蒂为蜷缩的样本共有8个(编号$1\sim5$，编号$12$、编号$16\sim17$)，即$m_{u,a} = 8$，根蒂为稍蜷的样本共有7个(编号$6\sim9$和编号$13\sim15$)，即$m_{u,b} = 7$;
设$i = 1$对应好瓜，$i = 2$对应坏瓜，好瓜中根蒂为蜷缩的样本共有5个(编号$1 \sim 5$)，即$m_{u, a,1} = 5$，好瓜中根蒂为稍蜷的样本共有3个(编号$6 \sim 8$)，即$m_{u,b,1} = 3$，坏瓜中根蒂为蜷缩的样本共有3个(编号12和编号$16\sim 17$)，即$m_{u,a,2} = 3$，坏瓜中根蒂为稍蜷的样本共有4个(编号9和编号$13\sim 15$.)，即为$m_{u,a,2} = 4$，因此VDM距离为

　　　　　　　　　$VDM_{p}(a, b) = \bigg|\frac{m_{u,a,1}}{m_{u,a}} - \frac{m_{u,a,1}}{m_{u,b}} \bigg|^p + \bigg|\frac{m_{u,a,2}}{m_{u,a}} - \frac{m_{u,b,2}}{m_{u,b}} \bigg|^p \\ = \bigg|\frac{5}{8} - \frac{3}{7}\bigg|^p + \bigg|\frac{3}{8} - \frac{4}{7} \bigg|^p$

对于混合属性可采用闵可夫斯基距离与VDM结合。
假定有$n_c$个有序属性、$n-n_c$个无序属性，不失一般性，令有序属性排列在无序属性之前，则

\[MinkovDM_p(x_i,x_j) = \left(\sum \limits_{u=1}^{n_c}|x_{iu}-x_{ju}|^p + \sum \limits_{u=n_c+1}^n VDM_p(x_{iu},x_{ju}) \right)^{\frac{1}{p}} \quad \quad (9.22) \]

其中$\displaystyle \sum_{u=1}^{n_c} |x_{iu}-x_{ju}|^p$表示有序属性，$\displaystyle \sum_{u=n_c+1}^n \text{VDM}_p(x_{iu},x_{ju})$表示无序属性。

当样本空间中不同属性的重要性不同时，可使用“加权距离”(weighted distance)。
以加权闵可夫斯基距离为例：

\[dist_{wmk}(x_i,x_j) = (w_1\cdot|x_{i1}-x_{j1}|^p + ... + w_n \cdot |x_{in} - x_{jn}|^p)^{\frac{1}{p}}. \quad \quad (9.23) \]

其中，权重$w_i \geq 0(i=1,2,...,n)$表征不同属性的重要性，通常$\sum_{i=1}^n w_i=1$.（定义域内所有属性的权重和为1）

需注意的是，通常我们是基于某种形式的距离来定义“相似度量”(similarity measure)，距离越大，相似度越小。距离越小，相似度越大然而，用于相似度度量的距离未必一定要满足距离度量的所有基本性质，尤其是直递性。

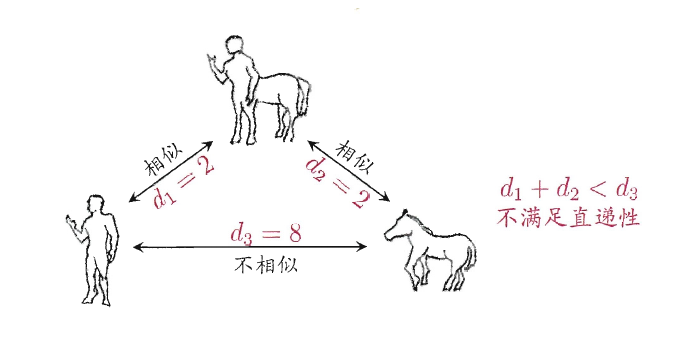
例如，在某些任务中我们可能希望有这样的相似度度量：
“人”，“马”分别是“人马”相似，但“人”与“马”很不相似；
要达到这个目的，可以令“人”，“马”与“人马”之间的距离都比较小，但“人”与“马”之间的距离很大，则此时该距离便不再满足直递性；这样的距离称为“非度量距离”(non-metric distance)。

(二)原型聚类

　　“原型”是指样本空间中具有代表性的点。
　　原型聚类，亦称“基于原型的聚类”(prototype-based clustering)，此类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用。通常情况下，算法先对原型进行初始化，然后对原型进行迭代更新求解。
采用不同的原型表示、不同的求解方式，将产生不同的算法。

2.1 $k$均值算法

　　给定样本集$D=\left\{x_1,x_2,...,x_m\right\}$，“$k$均值”(k-means)算法针对聚类所得簇划分$\mathcal{C}=\left\{C_1,C_2,...,C_k\right\}$最小化平方误差。

\[E = \sum \limits_{i=1}^k \sum \limits_{x∈C_i} ||x-\mu_i||_2^2 \quad \quad (9.24) \]

　　其中$\mu_i = \frac{1}{|C_i|}\sum_{x∈C_i}x$是簇$C_i$的均值向量。直观来看，上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，E值越小则簇内样本相似度越高。

　　求解最小化平方误差$E = \sum \limits_{i=1}^k \sum \limits_{x∈C_i} ||x-\mu_i||_2^2$并不容易，找到它的最优解需考察样本集D所有可能的簇划分，这是一个NP难(NPhard)问题。因此，$k$均值算法采用了贪心策略，通过迭代优化来近似求解E。

　　事实上，若将样本的类别看做为“隐变量”（latent variable），类中心看作样本的分布参数，这一过程正是通过EM算法的两步走策略而计算出，其根本的目的是为了最小化平方误差函数E：$E=\sum_{i=1}^k \sum_{x \in C_i}\|x-\mu_i\|_2^2$.

2.1.1 k-means算法描述

k-means算法流程如下所示:

输入：训练集$D=\{x_1,x_2,\ldots,x_m\}$；
聚类簇数$k$；
过程：
  1: 从$D$中随机选择$k$个样本作为初始均值向量$\{\mu_1,\mu_2,\ldots,\mu_k\}$
  2: repeat
  3:     令$C_i=\emptyset(1 \leqslant i \leqslant k)$
  4:      for $j=1,2,\ldots,m$ do
  5:         计算样本$x_i$与各均值向量$\mu_i(1 \leqslant i \leqslant k)$的距离：$d_{ji}=\|x_i-\mu_i\|_2$
  6:         根据距离最近的均值向量确定$x_j$的簇标记：$\lambda_j=\underset{i \in (1,2,\ldots,k)} {\arg \min} d_{ji}$
  7:         将样本$x_i$划入相应的簇：$C_{\lambda_j}=C_{\lambda_j} \cup \{x_j\}$

  8:     end for
  9:     for $i=1,2,\ldots,k$ do
  10:         计算新均值向量：$\displaystyle \mu'_i = \frac{1}{|C_i|} \sum_{x \in C_i} x$
  11:          if $\mu'_i \neq \mu_i$ then
  12:             将当前均值向量$\mu_i$更新为$\mu'_i$
  13:          else
  14:             保持当前均值向量不变
  15:         end if
  16:     end for
  17: until 当前均值向量均为更新
输出：簇划分$C=\{C_1,C_2,\ldots,C_k\}$.

　　其中第1行对均值向量进行初始化，在第4-8行与第9-16行依次对当前簇划分及均值向量迭代更新，若迭代更新后聚类结果保持不变，则在最后将当前簇划分结果返回。
　　

2.1.2 k-means算法应用实例

　　下面以西瓜数据集4.0为例来演示ｋ均值算法的学习过程。为方便叙述，我们将编号$i$的样本称为$x_i$，这是一个包含“密度”与“含糖率”两个属性值的二维向量。
　　

　　假定聚类簇数$k=3$，算法开始时随机选取三个样本$x_6,x_{12},x_{27}$作为均值向量，即

\[\mu_1 = (0.403; 0.237),\quad \mu = (0.343; 0.099), \quad \mu = (0.532; 0.472) \]

　　考察样本$x_1=(0.697; 0.237)$,，它与当前均值向量$\mu_1,\mu_2,\mu_3$的距离分别为0.369,0.506,0.166，因此$x_1$将被划入簇$C_3$中。类似的，对数据集中的所有样本考察一遍后，可得当前簇划分为

\[\begin{align} & C_1 = \left\{x_5,x_6,x_7,x_8,x_{9},x_{10},x_{13},x_{14},x_{15},x_{17},x_{18},x_{19},x_{20},x_{23} \right\}; \\ & C_2 = \left\{x_{11},x_{12},x_{16}\right\}; \\ & C_1 = \left\{x_1,x_2,x_3,x_4,x_{21},x_{22},x_{24},x_{25},x_{26},x_{27},x_{28},x_{29},x_{30}\right\}; \end{align} \]

　　于是，可从$C_1,C_2,C_3$分别求出新的均值向量

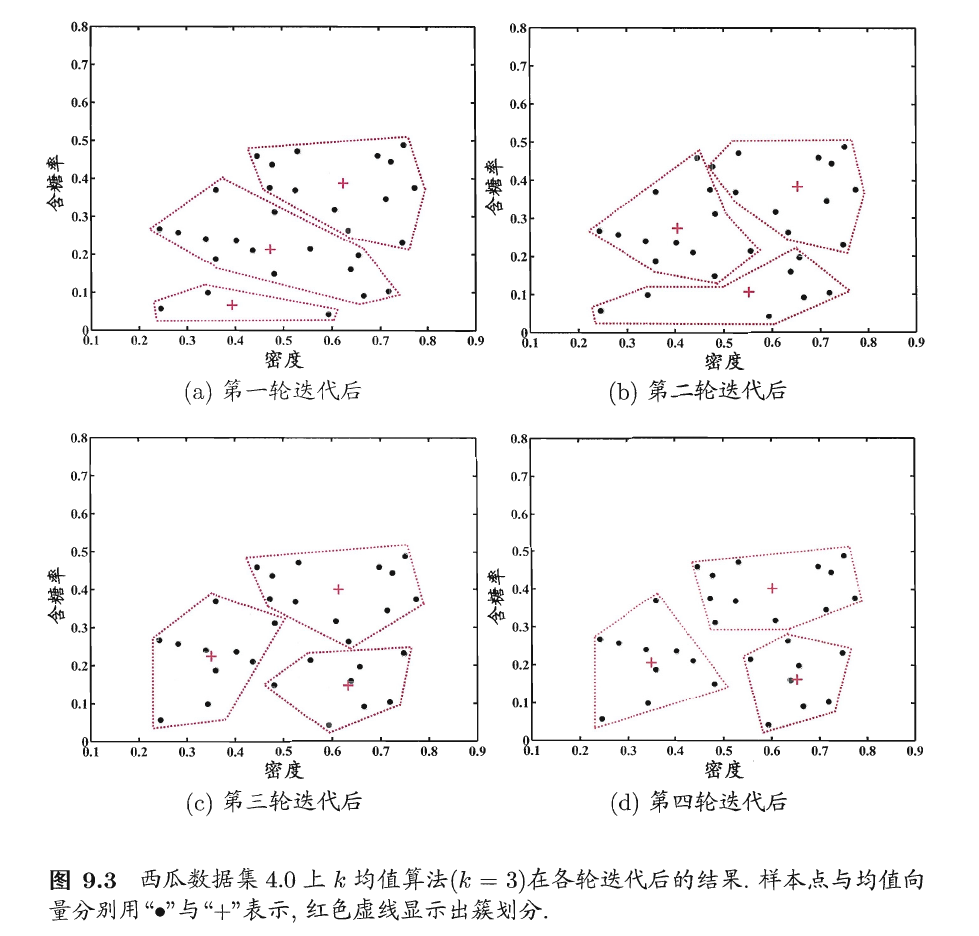
\[\mu_1' = (0.473; 0.214), \quad \mu_2' = (0.394; 0.066), \quad \mu_3' = (0.623; 0.388) \]

　　更新当前均值向量后，不断重复上述过程，如下图所示，第五轮迭代产生的结果与第四轮迭代相同，于是算法停止，得到最终的簇划分。

2.2 LVQ学习向量量化

LVQ也是基于原型的聚类算法，与K-Means不同的是，LVQ使用样本真实类标记辅助聚类，首先LVQ根据样本的类标记，从各类中分别随机选出一个样本作为该类簇的原型，从而组成了一个原型特征向量组，接着从样本集中随机挑选一个样本，计算其与原型向量组中每个向量的距离，并选取距离最小的原型向量所在的类簇作为它的划分结果，再与真实类标比较。

若划分结果正确，则对应原型向量向这个样本靠近一些
若划分结果不正确，则对应原型向量向这个样本远离一些

2.2.1 LVQ算法描述

　　与$k$均值算法类似，“学习向量量化”(Learning Vector Quantization，简称LVQ)也是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
　　
　　给定样本集$D=\left\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\right\}$，每个样本$x_j$是由n个属性描述的特征向量$x_{j1};x_{j2};...;x_{jn}，y_j∈\mathcal{Y}$是样本$x_j$的类别标记。LVQ的目标是学得一组n维原型向量{$p_1,p_2,...,p_q$}，每个原型向量代表一个聚类簇，簇标记$t_i∈\mathcal{Y}$。
　　

LVQ算法的流程如下所示：

输入：样本集$D=\{(x_1,y_1),(x_1,y_1),\ldots,(x_m,y_m)\}$；
原型向量个数$q$，各原型向量预设的类别标记$\{t_1,t_2,\ldots,t_q\}$
学习率$\eta$
过程：
  1: 初始化一组原型向量$\{p_1,p_2,\ldots,p_q\}$
  2: repeat
  3:     从样本集$D$随机选取样本$(x_j,y_j)$
  4:     计算样本$x_j$与$p_i(1 \leqslant i \leqslant q)$的距离：$d_{ij}=\|x_j-p_i\|_2$
  5:     找出与$x_j$距离最近的原型向量$p_{i^*}$，$\displaystyle i^*=\underset{i \in \{1,2,\ldots,q\}}{\arg \min} d_{ji}$
  6:     if $y_j = t_{i^*}$ then
  7:         $p'=p_{i^*} + \eta \cdot (x_j - p_{i^*})$ 可以理解为类中心向$x$靠近
  8:      else
  9:         $p'=p_{i^*} - \eta \cdot (x_j - p_{i^*})$ 类中心向$x$远离
10:     end if
11:     将原型向量$p_{i^*}$更新为$p'$
12: until 满足停止条件
输出：原型向量$\{p_1,p_2,\ldots,p_q\}$

　　算法第1行先对原型向量进行初始化，例如对第q个簇可从类别标记为$t_q$的样本中随机选取一个作为原型向量。算法第2$\sim$12行对原型向量进行迭代优化。在每一轮迭代中，算法随机选取一个有标记训练样本，找出与其距离最近的原型向量，并根据两者的类别标记是否一致来对原型向量进行相应的更新。在第12行中，若算法的停止条件已满足(例如已达到最大迭代轮数，或原型向量更新很小甚至不再更新)，则将当前原型向量作为最终结果返回。　　　　显然，LVQ的关键是第6-10行，即如何更新原型向量，直观上看，对样本$x_j$，若最近的原型向量$p_{i}$与$x_j$的类别标记相同，则令$p_{i}$向$x_j$的方向靠拢，如第7行所示，此时新原型向量为

\[p' = p_{i*} + \eta \cdot(x_j-p_{i*}) \quad \quad (9.25) \]

$p'$与$x_j$之间的距离为

\[||p'-x_j||_2 = ||p_{i*} + \eta \cdot (x_j-p_{i*})-x_j)||_2 \\ = (1-\eta)\cdot ||p_{i*}-x_j||_2. \quad \quad (9.26) \]

令学习率$\eta∈(0,1)$，则原型向量$p_{i*}$在更新为$p'$之后将更接近$x_j$.
　　
　　类似的，若$p_{i*}$与$x_j$的类别标记不同，则更新后的原型向量与$x_j$之间的距离将在增大为$(1+\eta)\cdot||p_{i*}-x_j||_2$，从而更远离$x_j$。
　　
　　在学得一组原型向量$\left\{p_1,p_2,...,p_q\right\}$后，即可实现对样本空间$\mathcal{X}$的簇划分。
　　对任意样本$x$，它将被划入与其距离最近的原型向量所代表的簇中；换言之，每个原型向量$p_i$定义了与之相关的一个区域$R_i$，该区域中每个样本与$p_i$的距离不大于它与其他原型向量$p_{i'}(i'\neq i)$的距离，即

\[R_{i} = \left\{x∈\mathcal{X} \bigg|||x-p_i||_2 \leq ||x-p_i'||_2, i' \neq i\right\}. \quad \quad (9.27) \]

由此形成了对样本空间的$\mathcal{X}$的簇划分$\left\{R_1,R_2,...,R_q\right\}$，该划分通常称为“Voronoi剖分”(Voronoi tessellation)。
　　

2.2.2 LVQ算法应用实例

　　下面以西瓜数据集4.0为例来演示LVQ算法的学习过程。
令9-21号样本的类别标记为$c_2$，其他样本的类别标记为$c_1$.假定$q=5$,即学习目标是找到5个原型向量$p_1,p_2,p_3,p_4,p_5$,并且假定其对应的类别标记分别为$c_1,c_2,c_2,c_1,c_1$．

　　算法开始时，根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化，假定初始化为样本$x_5,x_{12},x_{18},x_{23},x_{29}$.在第一轮迭代中，假定随机选取的样本$x_1$,该样本与当前原型向量$p_1,p_2,p_3,p_4,p_5$的距离分别为0.283,0.506,0.434,0.260,0.032.由于$p_5$与$x_1$距离最近的且两者具有相同的类别标记$c_2$，假定学习率$\eta=0.1$，则LVQ更新$p_5$得到新原型向量．

\[\begin{align} &p' = p_5 + \eta \cdot (x_1 - p_5) \\ &= (0.725; 0.445) + 0.1 \cdot((0.697; 0.460) - (0.725; 0.445)) \\ &= (0.722; 0.442) \end{align} \]

将$p_5$更新为$p'$后，不断重复上述过程，不同轮数之后的聚类结果如下图所示．

2.3 高斯混合聚类

2.3.1 高斯混合聚类算法推导

　　与k均值、LVQ用原型向量来刻画聚类结构不同，高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型。
　　我们先简单回顾一个(多元)高斯分布的定义。
　　对n维样本空间$\mathcal{X}$中的随机向量$x$，若$x$服从高斯分布，其概率密度函数为

\[p(x) = \frac{1}{(2\pi)^{\frac{n}{2}|\sum|^{\frac{1}{2}}}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)} \quad \quad (9.28) \]

其中$\mu$是n维均值向量，$\sum$是$n×n$的协方差矩阵。
　　由上式可看出，高斯分布完全由均值向量$\mu$和协方差矩阵$\sum$这两个参数确定。
为了明确显示高斯分布与相应参数的依赖关系，将概率密度函数记为$p(x|\mu,\sum)$.

式(9.28)的解释

　　该式就是多元高斯分布概率密度函数的定义式:
　　　　　　　　$p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}e^{-\frac{1}{2}(x - \mu)^T \sum^{-1}(x - \mu)}$

对应到我们常见的一元高斯分布概率密度函数的定义式:

$p(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其中$\sqrt{2\pi} = (2\pi)^{\frac{1}{2}}$对应于$(2\pi)^{\frac{n}{2}}$，$\sigma$对应$|\sum|^{\frac{1}{2}}$，指数项中分母中的方差$\sigma^2$对应协方差矩阵$\sum$,
$\frac{(x-\mu)^2}{\sigma^2}$对应$(x - \mu)^T\sum^{-1}(x - \mu)$。

　　概率密度函数$p(x)$是$x$的函数。其中对于某个特定的$x$来说，函数值$p(x)$就是一个数，若$x$的维度为2，则可以将函数$p(x)$的图像可视化，是三维空间的一个曲面。类似于一元高斯分布$p(x)$与横轴$p(x) = 0$之间的面积等于1(即$\int p(x)dx = 1$)，$p(x)$曲面与平面$p(x) = 0$之间体积等于1(即$\int p(x)dx = 1$)。
注意，西瓜书中后面将$p(x)$记为$p(x| \mu, \sum)$。

　　我们可定义高斯混合分布为

\[p_{\mathcal{M}}(x) = \sum \limits_{i=1}^k \alpha_i \cdot p(x|\mu_i, \begin{equation*}{\sum}_i\end{equation*}) \quad \quad (9.29) \]

　　该分布共由k个混合成分组成，每个混合成分对应于一个高斯分布。其中$\mu_i$与$\sum_i$是第$i$个高斯混合成分的参数，而$\alpha_i>0$为相应的“混合系数”(mixture coefficient)，$\sum_{i=1}^k \alpha_i=1$。

　　假设样本的生成过程由高斯混合分布给出：
首先，根据$\alpha_1,\alpha_2,...,\alpha_k$定义的先验分布选择高斯混合成分，其中$\alpha_i$为选择第$i$个混合成分的概率；
然后，根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。

式(9.29)的解释

　　对于该式表达的高斯混合分布概率密度函数$p_{\mathcal{M}}(x)$，与式$(9.28)$中的$p(x)$不同的是，它由$k$个不同的多元高斯混合分布加权而来。具体来说，$p(x)$仅由参数$\mu,\sum$确定，而$p_{\mathcal{M}}(x)$由k个“混合系数”$\alpha_i$以及$k$组参数$\mu_i, \sum_i$确定。
在上面的讨论中介绍了样本的生成过程，实际也反应了“混合系数”$\alpha_i$的含义，即$\alpha_i$为选择第$i$个混合成分的概率，或者反过来说，$\alpha_i$为样本属于第$i$个混合成分的概率。这里试着重新描述一下样本的的生成过程，根据先研验分布$\alpha_1, \alpha_2, ..., \alpha_k$选择其中一个高斯混合成分(即第$i$个高斯混合成分被选到的概率为$\alpha_i$)，假设选到第$i$个高斯混合成分，其参数为$\mu_i, \sum_i$；然后根据概率密度函数$p(x|\mu_i, \sum_i)$(即将式(9.28)中的$\mu, \sum$替换为$\mu_i,\sum_i$)进行采样生成样本$x$。两个步骤的区别在于第1步选择高斯混合成分时是从$k$个之中选其一(相当于概率密度函数是离散的)，而第2步生成样本时是从$x$定义域中根据$p(x|mu_i, \sum_i)$选择其中一个样本，样本被选中的概率即为$p(x|\mu_i,\sum_i)$。即第1步对应于离散型随机变量，第2步对应与连续型随机变量。

　　若训练集$D= \left\{x_1,x_2,...,x_m\right\}$由上述过程生成，令随机变量$z_j∈ \left\{1,2,...,k\right\}$表示生成样本$x_j$的高斯混合成分，其取值未知。显然，$z_j$的先验概率$P(z_j=i)$对应于$\alpha_i(i=1,2,...,k)$。
　　根据贝叶斯原理，$z_j$的后验分布对应于

\[p_{\mathcal{M}}(z_j=i|x_j) = \frac{P(z_j=i) \cdot p_{\mathcal{M}}(x_j|z_j=i)}{p_{\mathcal{M}}(x_j)} \\ = \frac{\alpha_i \cdot p(x_j|\mu_i, \sum_i)}{\sum \limits_{l=1}^k \alpha_l \cdot (x_j|\mu_l, \sum_l)}. \quad \quad (9.30) \]

　　其中，$p_{\mathcal{M}}(z_j=i | x_j)$是类先验，$p_{\mathcal{M}}(x_j | z_j=i)$是类条件。

换言之，$p_{\mathcal{M}}(z_j=i|x_j)$给出了样本$x_j$由第$i$个高斯混合成分生成的后验概率。

为方便叙述，将其简记为$\gamma_{ji}(i=1,2,...,k)$。

式(9.30)的解释

若由上述样本生成方式得到训练集$D = \left\{x_1, x_2,...,x_m \right\}$，那么现在的问题是对于给定样本$x_j$，它是由哪个高斯混合成分生成的呢?该问题即求后验概率$p_{\mathcal{M}}(z_j|x_j)$，其中$z_j \in \left\{1,2,...,k \right\}$。
下面对式(9.30)进行推导.
对于任意样本，在不考虑样本本身之前(即先验)，若试猜一下它由第$i$个高斯混合成分生成的概率$P(z_j = i)$，那么肯定按先验概率$\alpha_1, \alpha_2,...,\alpha_k$进行猜测，即$P(z_j = i) = \alpha_i$。若考虑样本本身带来的信息(即后验)，此时再试猜它由第$i$个高斯混合成分生成的概率$p_{\mathcal{M}}(z_j = i|x)$,根据贝叶斯公式，后验概率$p_{\mathcal{M}}(z_j = i|x_j)$可写为

　　　　　$p_{\mathcal{M}}(z_j = i|x_j) = \frac{P(z_j = i) \cdot p_{\mathcal{M}}(x_j | z_j = i)}{p_{\mathcal{M}}(x_j)}$

分子第1项$P(z_j = i) = \alpha_i$；第2项即第$i$个高斯混合成分生成样本$x_j$的概率$p(x_j|\mu_i, \sum)$，根据式(9.28)将$x, \mu,\sum$替换成$x_i,\mu_i, \sum_i$即得；分母$p_{\mathcal{M}}(x_j)$即为将$x_j$代入式(9.29)即得。
注意，西瓜书后面将$p_{\mathcal{M}}(z_j = i|x_j)$记为$\gamma_{ji}$，其中$1 \leq j \leq m, 1 \leq i \leq k$。

当高斯混合分布$p(x) = \frac{1}{(2\pi)^{\frac{n}{2}|\sum|^{\frac{1}{2}}}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}$已知时，高斯混合聚类将把样本集$D$划分为k个簇$\mathcal{C} = \left\{C_1,C_2,...,C_k\right\}$，每个样本$x_j$的簇标记$\lambda_j$如下确定：

\[\lambda_j = \mathop{\arg\max}_{i∈\left\{1,2,...,k\right\}}\gamma_{ji} \quad \quad (9.31) \]

式(9.31)的解释

若将所有$\gamma_{ji}$组成一个矩阵$\Gamma$，其中$\gamma_{ji}$为第$j$行第$i$列的元素，矩阵$\Gamma$大小为$m×k$，即
　　　　　　　　$\Gamma = \begin{bmatrix} \gamma_{11}& \gamma_{12}& \cdots & \gamma_{1k}\\ \gamma_{21}& \gamma_{22}& \cdots & \gamma_{2k}\\ \vdots & \vdots & \ddots & \vdots \\ \gamma_{m1}& \gamma_{m2}& \cdots & \gamma_{mk} \end{bmatrix}_{m×k}$

　其中$m$为训练集样本个数，$k$为高斯混合模型包含的混合模型个数。
可以看出，式(9.31)就是找出矩阵$\Gamma$中第$j$行的所有$k$个元素最大的那个元素的位置。
进一步说，式(9.31)就是最大后验概率。　

因此，从原型聚类的角度来看，高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画，簇划分则由原型对应后验概率确定。
　　那么，对于$p_{\mathcal{M}}(x) = \sum \limits_{i=1}^k \alpha_i \cdot p(x|\mu_i, \begin{equation*}{\sum}_i\end{equation*})$，模型参数${(\alpha_i,\mu_i,\sum_i)|1\leq i \leq k}$如何求解呢？
显然，给定样本集D，可采用极大似然估计，即最大化(对数)似然

\[LL(D) = ln \left(\prod_{j=1}^m p\mathcal{M}(x_j)\right) \\ = \sum \limits_{j=1}^m ln \left(\sum \limits_{i=1}^k \alpha_i \cdot p(x_j|\mu_i, \begin{equation*}{\sum}_i\end{equation*}) \right). \quad \quad (9.32) \]

式(9.32)的解释

　　对于训练集$D = \left\{x_1, x_2, ..., x_m \right\}$，现在要把$m$个样本划分为$k$个簇，即认为训练集D的样本是根据k个不同的多元高斯分布加权而得的高斯混合模型生成的。
　　现在的问题是，k个不同的多元高斯分布的参数$\left\{(\mu_i,\sum_i)| 1 \leq i \leq k\right\}$及它们各自的权重不知道，$m$归属于那个簇也不清楚，那么该怎么办呢?
　　其实这跟$k$均值算法类似，开始时既不知道$k$个簇的均值向量，也不知道$m$个样本归属于那个簇，最后我们采用了贪心策略，通过迭代优化来近似求解式(9.24)。
　　本节的高斯混合聚类求解方法与$k$均值算法，知识具体问题具体解法不同，从整体上来说，它们都应用了7.6节的期望最大化算法(EM算法)。
　　具体来说，现假设已知式(9.30)的后验概率，此时即可通过式(9.31)知道$m$个样本归属于哪个簇，再来求解参数$\left\{(\mu_i,\sum_i)| 1 \leq i \leq k\right\}$，该怎么求解呢? 对于每个样本$x_j$来说，它出现的概率是$p_{\mathcal{M}}(x_j)$，既然现在训练集合Ｄ中确实出现了$x_j$，我们当然希望待求解的参数$\left\{(\mu_i,\sum_i)| 1 \leq i \leq k\right\}$能够使这种可能性$p_{\mathcal{M}}(x_j)$最大；又因为我们假设$m$个样本是独立的，因此它们恰好一起出现的概率就是$\prod_{j=1}^m p_{\mathcal{M}}(x_j)$，既所谓的似然函数；
一般来说，连乘容易造成下溢(m个大于0小于1的数，当m较大时候，乘积会非常非常小，以至于计算机无法表达出这么小的数，从而产生下溢)，所以常用对数似然替代，即式(9.32)。

常采用EM算法进行迭代优化求解。下面我们做一个简单的推导。

若参数$\left\{(\alpha_i, \mu_i, \begin{equation*}{\sum}_i\end{equation*})| 1\leq i \leq k\right\}$能使$LL(D)$最大化，则由$\frac{\partial LL(D)}{\partial \mu_i} = 0$有

\[\sum \limits_{j=1}^m \frac{\alpha_i \cdot p(x_j|\mu_i,\begin{equation*}{\sum}_{i}\end{equation*})}{\sum \limits_{l=1}^k \alpha_l \cdot p(x_j|\mu_l,\begin{equation*}{\sum}_{l}\end{equation*})} (x_i-\mu_i) = 0. \quad \quad (9.33) \]

式(9.33)的推导

该式等号左侧即偏导$\frac{\partial LL(D)}{\partial \mu_i}$，下面先推导$\frac{\partial LL(D)}{\partial \mu_i}$的表达式。重写式(9.32)如下:

　　　　　　　　　　　　$LL(D) = \sum \limits_{j = 1}^m ln \left(\sum \limits_{l = 1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l) \right)$

这里将第2个求和号的求和变量由式(9.32)的$i$改成了$l$，这是为了避免与$p(x_j|\mu_j, \sum_i)$中的变量$i$相互混淆；
再次结合式(9.28)，重写$p(x_j|\mu_i, \sum_i)$的表达式如下:

$p(x_j|\mu_i, \sum_i) = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)}$

接下来开始推导$\frac{\partial LL(D)}{\partial \mu_i}$。根据链式求导法则

　　　　　　　　　　　$\frac{\partial LL(D)}{\partial \mu_i} = \frac{\partial LL(D)}{\partial p(x_j|\mu_i, \sum_i)} \cdot \frac{\partial p(x_j |\mu_i, \sum_i)}{\partial \mu_i}$

第1部分$\frac{\partial LL(D)}{\partial p(x_j|\mu_i, \sum_i)} $很容易进行求导:

　　　　　　　　　　　$\frac{\partial LL(D)}{\partial p (x_j|\mu_i, \sum_i)} = \frac{\partial \sum_{j=1}^m ln\left(\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l) \right)}{\partial p (x_j|\mu_i, \sum_i)} \\ = \sum \limits_{j=1}^m \frac{\partial ln \left(\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)\right)}{\partial p(x_j|\mu_i, \sum_l)} \\ = \sum \limits_{j=1}^m \frac{\alpha_i}{\sum_{l=1}^k \alpha_l \cdot p(x_j| \mu_l, \sum_l)}$

第二部分$\frac{\partial p(x_j |\mu_i, \sum_i)}{\partial \mu_i}$求导略显复杂：
　　　　　　　　　　$\frac{\partial p(x_j | \mu_i, \sum_i)}{\partial \mu_i} = \frac{\partial \frac{1}{(2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_{i}^{-1}(x_j - \mu_i)}}{\partial \mu_i} \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}}}\cdot \frac{\partial e^{-\frac{1}{2}}(x_j - \mu_i)^{T}\sum_i^{-1}(x_j - \mu_i)}{\partial \mu_i}$

上面仅把常数项拿出来，使求导形式看起来更直观一些；剩下的求导部分又是复合函数求导；

　　　　　　　　　$\frac{\partial e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}}{\partial \mu_i} = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)} \cdot \left(-\frac{1}{2} \frac{\partial(x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)}{\partial \mu_i} \right)$

又因为协方差矩阵的逆矩阵$\sum_{i}^{-1}$是对称阵，因此:

　　　　　　　　　$-\frac{1}{2} \frac{\partial(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}{\partial \mu_i} = -\frac{1}{2} \cdot 2 \sum_{i}^{-1}(\mu_i - x_j) = \sum_{i}^{-1}(x_i - \mu_j)$

因此第2部分求导结果为:

　　　　　　　　　$\frac{\partial p(x_j|\mu_i, \sum_i)}{\partial \mu_i} = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_j -\mu_i)^T \sum_i^{-1} (x_j - \mu_i)}\cdot \sum_{i}^{-1}(x_j - \mu_i) \\ = p(x_j|\mu_i, \sum_i) \cdot \sum_{i}^{-1}(x_j - \mu_i)$

综上所述

　　　　　　　　　$\frac{\partial LL(D)}{\partial \mu_i} = \sum \limits_{j=1}^m \frac{\alpha_i}{\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)} \cdot p(x_j|\mu_i, \sum_i) \cdot \sum_i^{-1} (x_j - \mu_i)$

注意$\sum_{i}^{-1}$对求和变量j来说是常量，因此可以提到求和号外面，当令$\frac{\partial LL(D)}{\partial \mu_i} = 0$时可以将该常量略掉(即等号两边同时左乘$\sum_i$)，即得式(9.33)：

　　　　　　　　$\frac{\partial LL(D)}{\partial \mu_i} = \frac{\alpha_i \cdot p(x_j|\mu_i, \sum_i)}{\alpha_l \cdot p(x_j|\mu_l, \sum_l)}(x_j - \mu_i) = 0 $

由于$p_{\mathcal{M}}$以及$\gamma_{ji}(z_j=i|x_j)$，有

\[\mu_i = \frac{\sum \limits_{j=1}^m \gamma_{ji}x_j}{\sum \limits_{j=1}^m \gamma_{ji}} \quad \quad (9.34) \]

即各混合成分的均值可通过样本加权平均来估计，样本权重是每个样本属于该成分的后验概率。

式(9.34)的推导

根据式(9.30)可知: $\gamma_{ji} = p_{\mathcal{M}}(z_j = i | x_j) = \frac{\alpha_i \cdot p(x_j|\mu_i, \sum_i)}{\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)}$

则式(9.33)可重写为: 　$\sum \limits_{j=1}^m \gamma_{ji}(x_j - \mu_i) = 0$
移项，得　　$\sum \limits_{j=1}^m \gamma_{ji}x_j = \sum \limits_{j=1}^m \gamma_{ji}\mu_i = \mu_i \cdot \sum \limits_{j=1}^m \gamma_{ji}$

第二个等号是因为$\mu_i$对于求和变量$j$来说是常量，因此可以提到求和号外面：
因此　$\mu_i = \frac{\sum \limits_{j=1}^m \gamma_{ji}x_j}{\sum \limits_{j=1}^m \gamma_{ji}}$得证。

类似的，由于$\frac{\partial LL(D)}{\partial \begin{equation*}{\sum}_i\end{equation*}} = 0$可得

\[\begin{equation*}{\sum}_i\end{equation*} = \frac{\sum \limits_{j=1}^m \gamma_{ji}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum \limits_{j=1}^m \gamma_{ji}}. \quad \quad (9.35) \]

式(9.35)的推导

该式推导过程与(9.33)(9.34)推导过程基本相同，根据链式求导法则
　　　　$\frac{\partial LL(D)}{\partial \sum_i} = \frac{\partial LL(D)}{\partial p(x_j|\mu_i, \sum_i)} \cdot \frac{\partial p(x_j|\mu_i, \sum_i)}{\partial \sum_i}$

第一部分与式(9.33)推导过程一样，第2部分与式(9.33)的区别较大且较为复杂:

　　　　　　$\frac{\partial p(x_j|\mu_i, \sum_i)}{\partial \sum_i} = \frac{\partial \frac{1}{(2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}}{\partial \sum_i} \\ = \frac{\frac{\partial e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}}{\partial \sum_i} \cdot (2\pi)^\frac{n}{2} |\sum_i|^\frac{1}{2}-e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)} \cdot \frac{\partial (2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}}}{\partial \sum_i}}{\left((2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}} \right)^2}$

上式看起来复杂，实际就是函数求导规则$(\frac{u}{v})' = \frac{u'v - uv'}{v^2}$；
下面先求分子中的两项求导:

　　　　$\frac{\partial e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}}{\partial \sum_i} = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)} - \frac{1}{2} \frac{\partial (x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)}{\partial \sum_i} \\ = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)} \cdot \frac{1}{2}\sum_{i}^{-T}(x_j - \mu_i)(x_j - \mu_i)^T \sum_i^{-T} \\ = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1} (x_j - \mu_i)} \cdot \frac{1}{2}\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T \sum_i^{-1}$

上式推导中，第一个等号就是运用了复合函数求导规则，其中$\frac{\partial(2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}}}{\partial |\sum_i|} = \frac{(2\pi)^{\frac{n}{2}}}{2}|\sum_i|^{-\frac{1}{2}}$；
第二个等号中的$\frac{\partial|\sum_i|}{\partial \sum_i} = |\sum_i| \cdot \sum_i^{-T}$为行列式求导，第二个等号是由于$\sum_i^{-1}$为对称阵。
为分子的两项求导结果代入

　　　　\(\frac{\partial p(x_j|\mu_i, \sum_i)}{\partial \sum_i} = \frac{\frac{\partial e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}}{\partial \sum_i} \cdot (2\pi)^{\frac{n}{2}}|\sum_i|^{\frac{1}{2}} - e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)}\cdot \frac{\partial (2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}}}{\partial \sum_i}}{\left((2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}} \right)^2} \\ = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)} \cdot \frac{\frac{1}{2}\sum_i^{-1}(x_j - \mu_i)(x_j - \mu_i)^T \sum_{i}^{-1} \cdot (2\pi)^{\frac{1}{2}} - \frac{(2\pi)^{\frac{n}{2}}}{2}|\sum_i|^{\frac{1}{2}} \cdot \sum_{i}^{-1}}{\left((2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}} \right)^2} \\ = e^{-\frac{1}{2}(x_j - \mu_i)^T \sum_i^{-1}(x_j - \mu_i)} \cdot \frac{\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T - I}{\left((2\pi)^\frac{n}{2}|\sum_i|^{\frac{1}{2}} \right)^2} \cdot \frac{(2\pi)^{\frac{n}{2}}}{2}|\sum_i|^{\frac{1}{2}} \cdot \sum_{i}^{-1} \\ = \frac{1}{(2\pi)^\frac{n}{2}|\sum_i|^\frac{1}{2}} e^{-\frac{1}{2}(x_j - \mu_i)^T\sum_i^{-1}(x_j - \mu_i)} \cdot \left(\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T - I\right) \cdot \frac{1}{2}\sum_{i}^{-1} \\ = p(x_j|\mu_i, \sum_i) \cdot \left(\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T - I \right) \cdot \frac{1}{2}\sum_{i}^{-1}\)

注意$\frac{(2\pi)^{\frac{n}{2}}}{2}|\sum_i|^{\frac{1}{2}}$为一个数，矩阵$I$为大小与协方差矩阵$\sum_{i}$相同的单位阵。

综上所述
　　　　$\frac{\partial LL(D)}{\partial \sum_i} = \sum \limits_{j=1}^m \frac{\alpha_i \cdot p(x_j |\mu_i, \sum_i)}{ \sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)} \cdot (\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T - I) \cdot \frac{1}{2}\sum_{i}^{-1} \\ = \sum_{j=1}^m \gamma_{ji} \cdot \left(\sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T - I \right) \cdot \frac{1}{2}\sum_{i}^{-1}$

移项，得　　$\sum \limits_{j=1}^m \gamma_{ji} \cdot \sum_{i}^{-1}(x_j - \mu_i)(x_j - \mu_i)^T = \sum_{j=1}^m \gamma_{ji}I$

两边同时左乘以$\sum_{i}$，得　$\sum_{j=1}^m \gamma_{ji} \cdot (x_j - \mu_i)(x_j - \mu_i)^T = \sum \limits_{j=1}^m \gamma_{ji}\sum_{i} = \sum_{i}\sum \limits_{j=1}^m \gamma_{ji}$

第二个等号是因为$\sum_{i}$对于求和变量$j$来说是常量，因此可以提到求和号外面；
因此　　$\sum_{i} = \frac{\sum \limits_{j=1}^m \gamma_{ji} \cdot (x_j - \mu_i)(x_j - \mu_i)^T}{\sum \limits_{j=1}^m \gamma_{ji}}$

对于混合系数$\alpha_i$，除了要最大化$LL(D)$，还需要满足$\alpha_i\geq 0,\sum_{i=1}^k \alpha_i=1$.
考虑$LL(D)$的拉格朗日形式.

\[LL(D) + \lambda \left(\sum \limits_{i=1}^k \alpha_i - 1\right) \quad \quad (9.36) \]

其中$\lambda$为拉格朗日乘子。

式(9.36)的解释

该式就是$LL(D)$添加了等式约束$\sum_{i=1}^k \alpha_i = 1$的拉格朗日形式。

由上式对$\alpha_i$的导数为0，有

\[\sum \limits_{j=1}^m \frac{p(x_j|\mu_i, \begin{equation*}{\sum}_i\end{equation*})} {\sum \limits_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \begin{equation*}{\sum}_{l}\end{equation*})} + \lambda = 0. \quad \quad (9.37) \]

式(9.37)的推导

重写式(9.32)如下: $LL(D) = \sum \limits_{j=1}^m ln \left(\sum \limits_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l) \right)$
这里将第2个求和号的求和变量由式(9.32)的$i$改为了$l$，这是为了避免对$\alpha_i$求导时与变量$i$相互混淆。
将式(9.36)中的两项分别对$\alpha_i$求导，得
　　$\frac{\partial LL(D)}{\partial \alpha_i} = \frac{\partial \sum_{j=1}^m ln \left(\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l) \right)}{\partial \alpha_i} \\ = \sum_{j=1}^m \frac{1}{\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)} \cdot \frac{\partial \sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)}{\partial \alpha_i} \\ = \sum_{j=1}^m \frac{1}{\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)} \cdot p(x_j|\mu_i, \sum_i)$

$\frac{\partial \left(\sum_{l=1}^k \alpha_l - 1 \right)}{\partial \alpha_i} = \frac{\partial(\alpha_1 + \alpha_2 + ... + \alpha_i + ... + \alpha_k - 1)}{\partial \alpha_i} = 1$

综合两项求导结果，并令导数等于零即得式(9.37)

两边同乘以$\alpha_i$，对所有混合成分求和可知$\lambda=-m$，有

\[\alpha_i = \frac{1}{m} \sum \limits_{j=1}^m \gamma_{ji} \quad \quad (9.38) \]

即每个高斯成分的混合系数由样本属于该成分的平均后验概率确定。

式(9.38)的推导

对式(9.37)两边同乘以$\alpha_i$，得 $\sum \limits_{j=1}^m \frac{\alpha_i p(x_j|\mu_i, \sum_i)}{\sum_{l=1}^k \alpha_l \cdot p(x_j| \mu_l, \sum_l)} + \lambda \alpha_i = 0$
结合式(9.30)发现，求和号内即为后验概率$\gamma_{ji}$，即　$\sum_{j=1}^m \gamma_{ji} + \lambda \alpha_i = 0$

对所有混合成分求和，得 $\sum \limits_{i=1}^k \sum \limits_{j=1}^m \gamma_{ji} + \sum \limits_{i=1}^k \lambda \alpha_i = 0$
注意$\sum \limits_{i=1}^k \alpha_i = 1$，因此$\sum_{i=1}^k \lambda \alpha_{i} = \lambda \sum_{i=1}^k \alpha = \lambda$，
根据式(9.30)中$\gamma_{ji}$表达式可知

　　　$\sum \limits_{i=1}^k \gamma_{ji} = \frac{\alpha_i \cdot p(x_j|\mu_j , \sum_i)}{\sum_{l=1}^k \alpha_l \cdot p(x_j|\mu_l, \sum_l)} \\ = \frac{\sum_{i=1}^k \alpha_i \cdot p(x_j|\mu_i, \sum_i)}{\alpha_l \cdot p(x_j|\mu_l, \sum_l)} \\ = 1$

再结合加法满足交换律，所以　$\sum \limits_{i=1}^k \sum \limits_{j=1}^m \gamma_{ji} = \sum \limits_{j=1}^m \sum \limits_{i=1}^k \gamma_{ji} = \sum \limits_{j=1}^m 1 = m$

将以上分析结果代入$\sum_{i=1}^k \sum_{j=1}^m \gamma_{ji} + \sum_{i=1}^k \lambda \alpha_i = 0$，移项即得$\lambda = -m$。
将此结果代入$\sum_{j=1}^m \gamma_{ji} + \lambda \alpha_i = 0$，即$\sum_{j=1}^m \gamma_{ji} - m\alpha_i = 0$，整理即可得式(9.38)

　　由上述推导即可获得高斯混合模型的EM算法：
在每步迭代中，
(E步): 先根据当前参数来计算每个样本属于每个高斯成分的后验概率$p_{\mathcal{M}}$(即$\gamma_{ji}$，第$i$个样本属于$j$类)，
(M步):再根据$\mu_i$,$\begin{equation*}{\sum}_i\end{equation*}$,$\alpha_i$更新模型参数$\left\{(\alpha_i,\mu_i,\begin{equation*}{\sum}_i\end{equation*})| 1\leq i \leq k\right\}$.

\[\begin{align} &\mu_i=\frac{\displaystyle \sum_{j=1}^m \gamma_{j i} x_j}{\displaystyle \sum_{j=1}^m \gamma_{j i}} \\ & \alpha_{i}=\frac{1}{m} \sum_{j=1}^m \gamma_{j i} \\ &\Sigma_i=\frac{\displaystyle \sum_{j=1}^m \gamma_{j i}(x_j-\mu_i)(x_j-\mu_i)^T}{\displaystyle \sum_{j=1}^m \gamma_{j i}} \end{align} \]

2.3.2 高斯混合聚类算法描述

　高斯混合聚类的算法流程如下所示：

输入：样本集$D=\{x_1,x_2,\ldots,x_m\}$；
高斯混合成分个数$k$
过程：
  1: 初始化高斯混合分布的模型参数$\{(\alpha_i,\mu_i,\Sigma_i) | 1 \leqslant i \leqslant k\}$
  2: repeat
  3:     for $j=1,2,\ldots,m$ do
  4:         根据式（1）计算$x_i$由各混合成份生成的后验概率，即$\gamma_{ji}=P_M(z_j=i | x_j) (1 \leqslant i \leqslant k)$ (E步)
  5:      end for
  6:      for $i=1,2,\ldots,k$ do (M步)
  7:          计算新均值向量：$\mu'_i=\frac{\displaystyle \sum_{j=1}^m \gamma_{j i} x_j}{\displaystyle \sum_{j=1}^m \gamma_{j i}}$
  8:         计算新协方差矩阵：$\Sigma'_i=\frac{\displaystyle \sum_{j=1}^m \gamma_{j i}(x_j-\mu_i)(x_j-\mu_i)^T}{\displaystyle \sum_{j=1}^m \gamma_{j i}}$
  9:         计算新混合系数：$\displaystyle \alpha'_{i}=\frac{1}{m} \sum_{j=1}^m \gamma_{j i}$
10:     end for
11:     将模型参数$\{(\alpha_i, \mu_i, \Sigma_i) | 1 \leqslant i \leqslant k\}$更新为$\{(\alpha'_i, \mu'_i, \Sigma'_i) | 1 \leqslant i \leqslant k\}$
12: until 满足停止条件
13: $C_i = \varnothing(1 \leqslant i \leqslant k)$

14: for j=1,2,...,m　do
15:    根据$\lambda_j=\underset{i \in\{1,2, \ldots, k\}}{\arg \max } \gamma_{j i}$确定$x_i$的簇标记$\lambda_j$
16:     将$x_j$划入相应的簇：$C_{\lambda_j} = C_{\lambda_j} \cup \{x_j\}$
17: end for
输出：簇划分$C=\{C_1,C_2,\ldots,C_k\}$

　　算法第1行对高斯混合分布的模型参数进行初始化，然后，在2-12行基于EM算法对模型参数进行迭代更新。若EM算法停止条件满足(例如已达到最大迭代轮数，或似然函数LL(D))增长很少甚至不再增长)，则在第14-17行根据高斯混合分布确定簇划分，在第18行返回最终结果。

高斯混合聚类算法描述的解释说明

第1行初始化参数，按如下策略进行初始化:
混合系数$\alpha_i = \frac{1}{k}$；任选训练集中的$k$个样本分别初始化$k$个均值向量$\mu_i(1 \leq i \leq k)$；
使用对角元素为0.1的对角阵初始化$k$个协方差矩阵$\sum_i(1 \leq i \leq k)$。
第3-5行根据式(9.30)计算共$m×k$个$\gamma_{ji}$。
第6-10行分别根据式(9.34)、式(9.35)、式(9.38)使用刚刚计算得到的$\gamma_{ji}$更新均值向量、协方差矩阵、混合系数；
注意第8行计算协方差矩阵使用的是第7行计算得到的均值向量，这是因为协方差矩阵$\sum_{i}'$与均值向量$\mu_i'$是对应的，而非$\mu_i$;第7行的$\mu_i'$在第8行使用之后会在下一轮迭代中第4行计算$\gamma_{ji}$再次使用。
整体来说，第2-12行就是一个EM算法的具体使用例子，学习完7.6节EM算法可能跟本无法理解其实现那个。此例中有两组变量，分别是$\gamma_{ji}$和$(\alpha_i, \mu_i, \sum_i)$，然后计算$\gamma_{ji}$；再根据$\gamma_{ji}$根据最大似然推导出的公式更新$(\alpha_i, \mu_i, \sum_i)$，反复迭代，直到满足停止条件。

2.3.3 高斯混合聚类算法应用实例

下面以西瓜数据集4.0为例来演示高斯混合聚类算法的学习过程。
令高斯混合成分的个数$k=3$。算法开始时，假定将高斯混合分布的模型参数初始化为：
　　$\alpha_1=\alpha_2=\alpha_3=\frac{1}{3}$;
　　$\mu_1 = x_6, \mu_2 = x_{22}, \mu_3 = x_{27}$;
　　$\sum_1 = \sum_2 = \sum_3 = \begin{pmatrix} 0.1 & 0.0 \\ 0.0 & 0.1 \end{pmatrix}$.
在第一轮迭代中，先计算样本由各混合成分生成的后验概率。
以$x_1$为例，由于$p_{\mathcal{M}}(z_j=i|x_j) = \frac{P(z_j=i) \cdot p_{\mathcal{M}}(x_j|z_j=i)}{p_{\mathcal{M}}(x_j)} = \frac{\alpha_i \cdot p(x_j|\mu_i, \sum_i)}{\sum \limits_{l=1}^k \alpha_l \cdot (x_j|\mu_l, \sum_l)}$算出后验概率
　　$\gamma_{11}=0.219, \gamma_{12}=0.404,\gamma_{13}=0.377$.

将所有样本的后验概率算完后，得到如下新的模型参数：

\[\alpha_1' = 0.361, \quad \alpha_2' = 0.323, \quad \alpha_3' = 0.316 \\ \mu_1' = (0.491; 0.251), \quad \mu_2' = (0.571; 0.281), \quad \mu_3' = (0.534; 0.295) \\ \]

$\sum_1' = \begin{pmatrix} 0.025 & 0.004 \\ 0.004 & 0.016 \end{pmatrix}, \sum_2' = \begin{pmatrix} 0.023 & 0.004 \\ 0.004 & 0.017 \end{pmatrix}, \sum_3' = \begin{pmatrix} 0.024 & 0.005 \\ 0.005 & 0.016 \end{pmatrix}$.

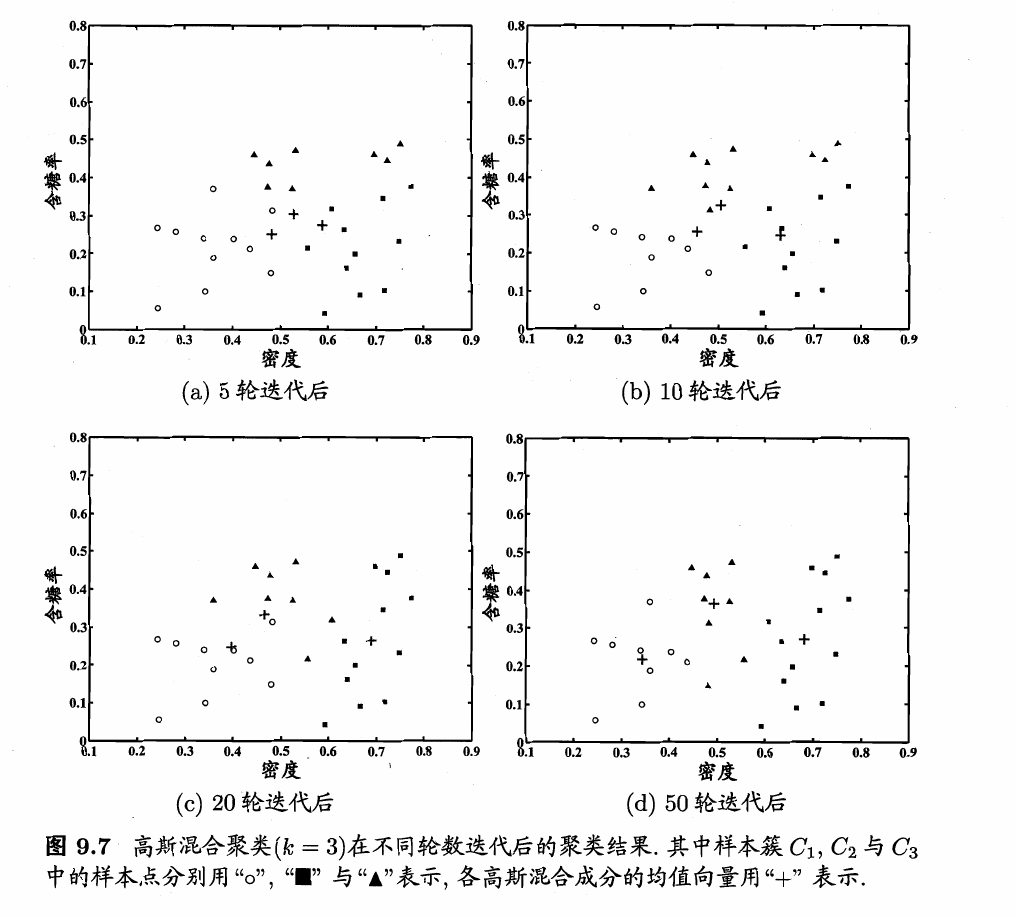
模型参数更新后，不断重复上述过程，不同的轮数之后的聚类结果，如下图所示。

(三)密度聚类

3.1 密度聚类基本概念

　　密度聚类亦称为“基于密度的聚类”(density-based clustering)，此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
　　
　　DBSCAN是一种著名的密度聚类算法，它基于一组“邻域”(neigh-borhood)参数($\epsilon，MinPts$)来刻画样本分布的紧密程度。给定数据集$D=\left\{x_1,x_2,...,x_m\right\}$，定义下面这几个概念。

$\epsilon-$邻域：对$x_j∈D$，其$\epsilon-$邻域包含样本集D中与$x_j$的距离不大于$\epsilon$的样本，即$N_{\epsilon}={x_i∈D|dist(x_i,x_i)\leq \epsilon}$;
核心对象(core object)：若$x_j$的$\epsilon-$邻域至少包含$MinPts$个样本，即$|N_{\epsilon}(x_j)|\geq MinPts$，则$x_j$是一个核心对象；
密度可达(directly density-reachable)：若$x_j$位于$x_i$的$\epsilon-$邻域中，且$x_i$是核心对象，则称$x_j$由$x_i$密度可达；
密度相连(density-reachable)：对$x_i$与$x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$x_i$与$x_j$密度相连。

下图给出了上述概念的直观显示。

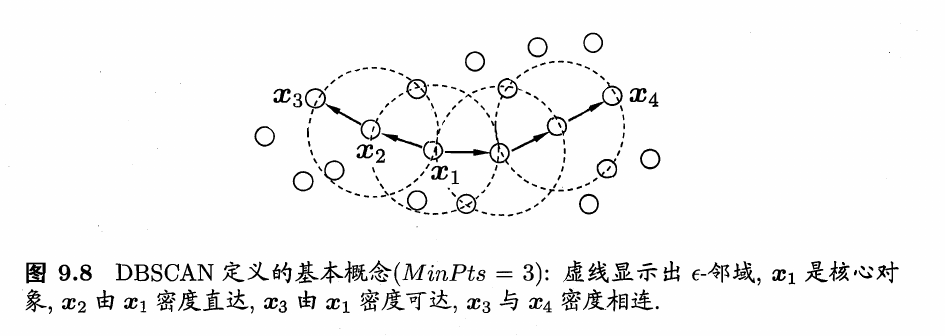
基于这些概念，DBSCAN将“簇”定义为：由密度可达关系导出的最大的密度相连样本集合。形式化地说，给定邻域参数$(\epsilon,MinPts)$，簇$Ｃ\subseteq D$是满足以下性质的非空样本子集：

连接性(connectivity): $x_i∈C$,$x_j∈C\Rightarrow$ $x_i$与$x_j$密度相连
最大性(maximality):$x_i∈C$,$x_j$由$x_i$密度可达$x_i∈C\Rightarrow$$x_j∈C$。

那么，如何从数据集Ｄ中找出满足以上性质的聚类簇呢？实际上，若x为核心对象，由x密度可达的所有样本组成的集合记为$X=\left\{x'∈D|x‘是由于x密度可达\right\}$,则不难证明Ｘ即为满足连接性与最大性的簇。

于是，如何从数据集Ｄ中任选数据集中的一个核心对象为“种子”(seed)，再由此出发确定相应的聚类簇。

3.2 DBSCAN算法描述

　　简单来理解DBSCAN便是：找出一个核心对象所有密度可达的样本集合形成簇。首先从数据集中任选一个核心对象$A$，找出所有$A$密度可达的样本集合，将这些样本形成一个密度相连的类簇，直到所有的核心对象都遍历完。

DBSCAN算法的流程如下图所示：

输入：样本集$D=\{x_1,x_2,\ldots,x_m\}$；
邻域参数$(\epsilon, MinPts)$
过程：
  1: 初始化核心对象集合：$\Omega=\emptyset$
  2: for $j=1,2,\ldots,m$ do
  3:     确定样本$x_j$的$\epsilon$-邻域$N_{\epsilon}(x_j)$
  4:     if $|N_{\epsilon(x_j)}| \geqslant MinPts$ then
  5:         将样本$x_j$加入核心对象集合：$\Omega=\Omega \cup \{x_j\}$
  6:      end if
  7: end for
  8: 初始化聚类簇数：$k=0$
  9: 初始化未访问样本集合：$\Gamma = D$
10: while $\Omega \neq \emptyset$ do
11:     记录当前未访问样本集合：$\Gamma_{\text{old}} = \Gamma$；
12:     随机选取一个核心对象$o \in \Omega$，初始化队列$Q=<o>$；
13:     $\Gamma = \Gamma \backslash \{o\}$；
14: while $Q \neq \emptyset$ do
15:         取出队列$Q$中的首个样本$q$；
16:         if $|N_{\epsilon}(q)| \geqslant MinPts$ then
17:             令$\Delta=N_{\epsilon}(q) \cap \Gamma$；
18:             将$\Delta$中的样本加入队列$Q$；
19:             $\Gamma = \Gamma \backslash \Delta$；
20:         end if
21:     end while
22:      $k=k+1$，生成聚类簇$C_k=\Gamma_{\text{old}} \backslash \Gamma$；
23:     $\Omega = \Omega \backslash C_k$
24: end while
输出：簇划分$C=\{C_1,C_2,\ldots,C_k\}$

其中1-7是找出所有核心对象，16是判定是否为核心对象，17是找出其邻域内的样本，即密度直达，
22是核心对象$o$所有密度可达的样本集合，23是直到遍历完所有核心对象。

3.3 DBSCAN算法应用实例

下面以西瓜数据集4.0为例来演示DBSCAN聚类算法的学习过程。
假定邻域参数$(\epsilon,MinPts)$设置为$\epsilon=0.11,MinPts=5$。
DBSCAN算法先找出合样本的$\epsilon-$邻域并确定核心对象集合：$\Omega=\left\{x_3,x_5,x_6,x_8,x_9,x_{13},x_{14},x_{18},x_{19},x_{24},x_{28},x_{29}\right\}$。
然后，从$\Omega$中随机选取一个核心对象作为种子，找出由它密度可达的所有样本，这就构成了第一个聚类簇。
不失一般性，假定核心对象$x_8$被选中作为种子，则$DBSCAN$生成的第一个聚类簇为

\[C_1 = \left\{x_6, x_7, x_8, x_{10}, x_{12}, x_{18}, x_{19}, x_{20}, x_{23} \right\} \]

然后，DBSCAN将$C_1$中包含的核心对象从$\Omega$中去除：$\Omega=\Omega$\ $C_1$＝{$x_3,x_5,x_9,x_{13},x_{14},x_{24},x_{25},x_{28},x_{29}$}再从更新后的集合$\Omega$中随机选取一个核心对象作为种子来生成下一个聚类簇。上述过程不断重复，直至$\Omega$为空。

下图显示出DBSCAN先后生成聚类簇的情况。

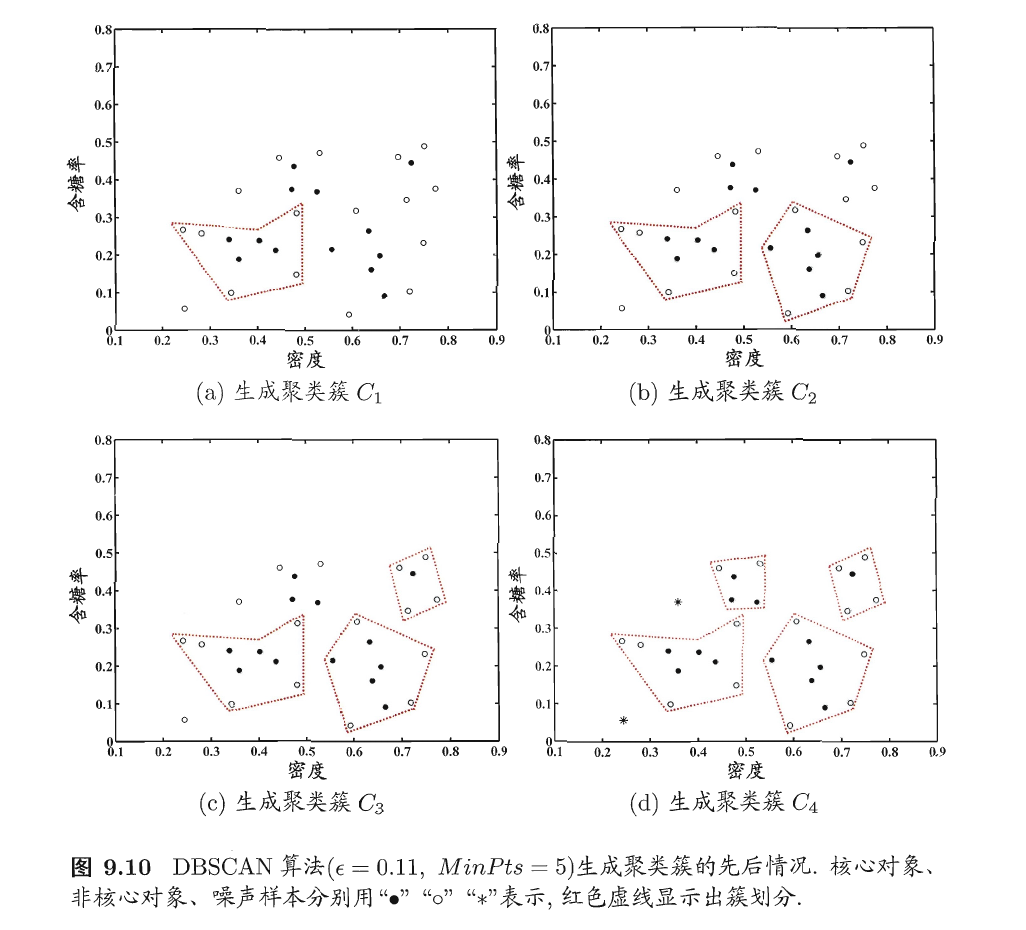
$C_1$之后生成的聚类簇为

\[\begin{align} & C_2 = \left\{x_3, x_4, x_5, x_9, x_{13}, x_{14}, x_{16}, x_{17}, x_{21} \right\}; \\ & C_3 = \left\{x_1, x_2, x_{22}, x_{26}, x_{26} \right\}; \\ & C_4 = \left\{x_{24}, x_{25}, x_{27}, x_{28}, x_{30} \right\}. \end{align} \]

DBSCAN聚类算法的辨析

我们这里回顾一下，前面所介绍的聚类算法通常只能产生“凸聚类”，而这里介绍的DBSCAN聚类算法则能产生“非凸聚类”，其本质原因，在于聚类时使用的距离度量不同，例如$k$均值算法使用欧氏距离，而DBSCAN使用类似于测地线距离(注意只是类似，并不完全是测地线距离)，因此可以产生如下距离结果(中间为典型的非凸聚类):

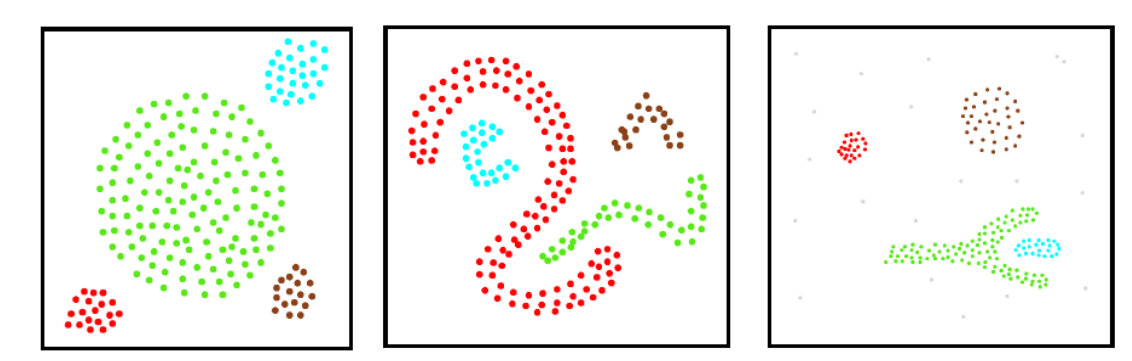
注意：虽然左图为“凸聚类”(四个簇都有一个凸包)，但k均值算法却无法产生此结果，因为最大的簇过于大，其外围样本与另三个小簇的中心之间的距离更近，因此中间的最大的簇肯定会被$k$均值算法划分到不同的簇之中，这显然不是我们希望的结果。
密度聚类算法可以产生任意形状的簇，不需要事先指定聚类个数$k$，并且对噪声鲁棒。

这里区分三个概念：

密度直达、密度可达、密度相连

　　由$x_i$密度直达，该概念最容易理解，但要特别注意：密度直达除了要求$x_j$位于$x_i$的$\epsilon-$领域的条件之外，还额外要求$x_i$是核心对象；$\epsilon-$领域满足对称性，但$x_j$不一定为核心对象，因此密度直达关系通常不满足对称性。

　　$x_j$由于$x_i$密度可达，该概念基于密度直达，因此样本序列$p_1, p_2,...,p_n$中除了$p_n = x_j$之外，其余样本均为核心对象(当然包括$p_1 = x_i$)，所以同理，一般不满足对称性.

　　以上两个概念中，若$x_j$为核心对象，已知$x_j$由$x_i$密度直达/可达，则$x_i$由$x_j$密度直达/可达，即满足对称性(也就是说，核心对象之间的密度直达/可达对称性)。
　　$x_i$与$x_j$密度相连，不要求$x_i$与$x_j$为核心对象，所以满足对称性。

(四)层次聚类

　　层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。

4.1 AGNES基本概念

　　AGNES是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作是一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。

假设有$N$个待聚类的样本，数据集$D$可简单表示为{$(x_1,x_2,...,x_{N})$}，其基本步骤为：

初始化$\to$数据集中的每个样本看作是一个初始聚类簇(归于一类)($x_1\to C_1$)
即将$D=\left\{(x_1,x_2,...,x_{N})\right\}$对应于$D=\left\{(C_1,C_2,...,C_{N})\right\}$.

迭代过程=> 迭代过程划分为若干个子过程，在算法运行的每一步执行以下子过程：
子过程=> 距离合并计算$\to$寻找距离最近的两个聚类簇进行合并(合并后类的总数就减少一个)
更新生成的聚类簇与其余簇之间的距离(相似度)。

达到终止条件，跳出迭代，结束过程。
终止条件为：当前聚类簇个数达到预设的聚类簇个数。

　　这里的关键是如何计算聚类簇之间的距离。实际上，每个簇是一个样本集合，因此，只需采用关于集合的某种距离即可。例如，给定聚类簇$C_i$和$C_j$，可通过下面的式子来计算距离：

\[\begin{align} & 最小距离：d_{min}(C_i,C_j) = \underset{x∈C_i,z∈C_j}{min} dist(x,z) \quad \quad (9.41) \\ & 最大距离：d_{max}(C_i,C_j) = \underset{x∈C_i,z∈C_j}{max} dist(x,z) \quad \quad (9.42) \\ & 平均距离：d_{avg}(C_i,C_j) = \frac{1}{|C_i||C_j|} \sum \limits_{x∈C_i}\sum \limits_{z∈C_j} dist(x,z). \quad \quad (9.43) \end{align} \]

根据上式关系，显然，最小距离$d_{min}$由两个簇的最近样本决定，
最大距离$d_{max}$由两个簇的最远样本决定，而平均距离$d_{avg}$则由两个簇的所有样本共同决定。

其中，当聚类簇距离由$d_{min}$计算时，AGNES算法被相应地称为“单链接”(single-linkage)算法
当聚类簇距离由$d_{max}$计算时，AGNES算法被相应地称为“全链接”(complete-linkage)算法
当聚类簇距离由$d_{avg}$计算时，AGNES算法被相应地称为“均链接”(average-linkage)算法。

4.2 AGNES算法描述

层次聚类法的算法流程如下所示：

输入：样本集$D=\{x_1,x_2,\ldots,x_m\}$；
聚类簇距离度量函数$d$；
聚类簇数$k$；
过程：
  1: for $j=1,2,\ldots,m$ do
  2: $C_j=\{x_j\}$
  3: end for
  4: for $i=1,2,\ldots,m$ do
  5: for $j=1,2,\ldots,m$ do
  6: $M(i,j)=d(C_i,C_j)$；
  7: $M(j,i)=M(i,j)$
  8: end for
  9: end for
10: 设置当前聚类簇个数：$q=m$
11: while $q > k$ do
12: 找出距离最近的两个聚类簇$C_{i^*}$和$C_{j^*}$
13: 合并$C_{i^*}$和$C_{j^*}$：$C_{i^*} = C_{i^*} \cup C_{j^*}$
14: for $j=j^*+1,j^*+2,\ldots,q$ do
15: 将聚类簇$C_j$重编号为$C_{j-1}$
16: end for
17: 删除距离矩阵$M$的第$j^*$行与第$j^*$列；
18: for $j=1,2,\ldots,q-1$ do
19: $M(i^*,j)=d(C_{i^*},C_j)$；
20: $M(j,i^*)=M(i^*,j)$
21: end for
22: $q=q-1$
23: end while
输出：簇划分$C=\{C_1,C_2,\ldots,C_k\}$

AGNES算法如上所示。在第1-9行，算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化；然后在第11-23行，AGNES不断合并距离最近的聚类簇，并对合并得到的聚类簇的距离矩阵进行更新；上述过程不断重复，直至达到预设的聚类簇数。

AGNES算法描述的解释说明

　　在第1-7行中，算法先根据给定的领域参数$(\epsilon, MinPts)$找出所有核心对象，并存于集合$\Omega$之中；第4行的$if$判断语句即在判别$x_j$是否为核心对象。
　　在第10-24行中，以任一核心对象为出发点(由12行实现)，找出其密度可达的样本生成聚类簇(由第14-21行实现)，直到所有核心对象被访问为止(由第10行和第23行配合实现)。
　　具体来说：
　　其中第14-21行while循环中的if判断语句(第16行)在第一次训练时一定为真(因为$Q$在第12行初始化为某核心对象)，此时会往队列$Q$在第12行初始化为某核心对象)，此时会往队列Q中加入$q$密度直达的样本(已知$q$为核心对象，$q$的$\epsilon-$领域中的样本即为$q$密度直达的)，队列遵循先进先出规则，接下来的循环将依次判别依次判别$q$的$\epsilon$领域中的样本是否为核心对象(第 16 行)，若为核心对象,则将密度直达的样本( $\epsilon-$领域中的样本)加入$Q$ 。根据密度可达的概念,while 循环中的 if 判断语句(第16 行)找出的核心对象之间一定是相互密度可达的,非核心对象一定是密度相连的。
　　第14-21行while循环每跳出一次，即生成一个聚类簇。每次生成聚类簇之前，会距离当前未访问过样本集合(第11行$\Gamma_{old} = \Gamma$)，然后当前要生成的聚类簇每决定录取一个样本后会将该样本从$\Gamma$中去除(第13行和第19行)，因此第14-21行while循环每跳出一次后，$\Gamma_{old}$与$\Gamma$差别即为聚类簇的样本成员(第22行)，并将该聚类簇中的核心对象从第1-7行生成的核心对象集合$\Omega$中去除。
　　符号“\”为集合求差，例如集合$A = \left\{a,b,c,d,e,f \right\}$，$B = \left\{a,d,f,g,h \right\}$，则A \ B为A \ B$=\left\{b,c,e \right\}$，即将A,B所有相同的元素从A中去除。

4.3 AGNES算法应用实例

　　以西瓜数据集4.0为例，令AGNES算法一直执行到所有样本出现在同一个簇中，即k=1，则可得到下图所示的“树状图”(dendrogram)，其中每层链接一组聚类簇。

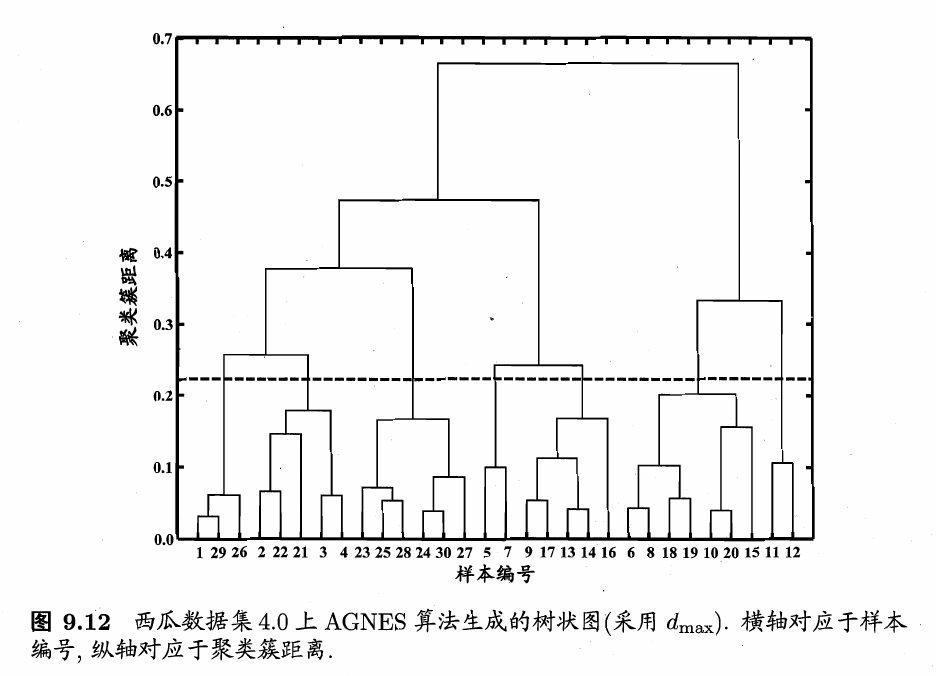
在树状图的特定层次上进行分割，则可得到相应的簇划分结果。例如，以图9.12中所示虚线分割树状图，将得到包含7个聚类簇的结果：

\[\begin{align} &C_1 = \left\{x_1, x_{26}, x_{26} \right\}; \quad C_2 = \left\{x_2, x_3, x_4, x_{21}, x_{22} \right\};\\ &C_3 = \left\{x_{23}, x_{24}, x_{25}, x_{27}, x_{28}, x_{30}\right\}; \quad C_4 = \left\{x_5, x_7 \right\}\\ &C_5 = \left\{x_9, x_{19}, x_{14}, x_{16}, x_{17}; \\ C_6 = \left\{x_6, x_8, x_{10}, x_{15}, x_{18}, x_{19}, x_{20} \right\}\right\}; \\ &C_7 = \left\{x_11, x_{12} \right\} \end{align} \]

将分割层逐步提升，则可得到聚类簇逐渐减少的聚类结果。例如下图9.13显示出了从图9.12中产生了7至4个聚类簇的划分结果。

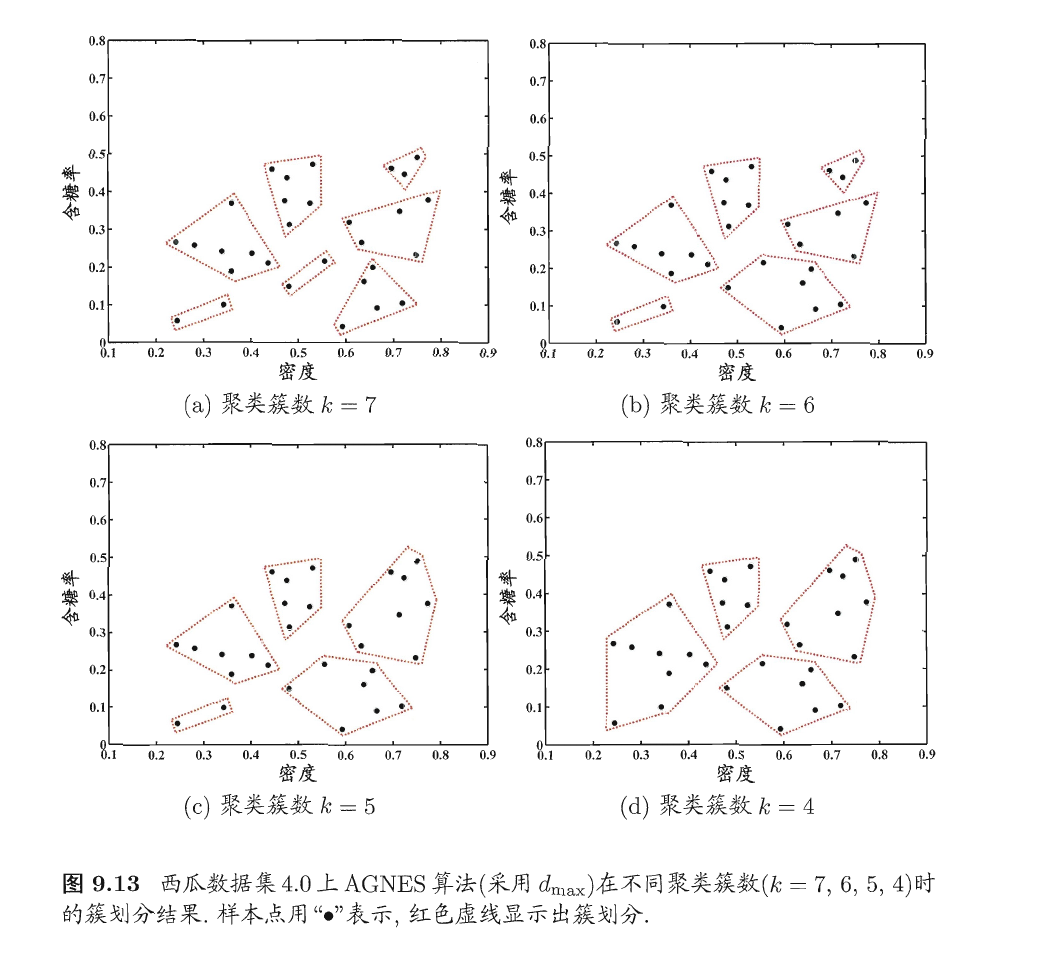
(五)本章小结

　　与其他机器学习算法相比，聚类也许是机器学习中“新算法”出现最多、最快的领域。
　　一个重要原因是聚类不存在客观标准；给定数据集，总能从某个角度找到以往算法未覆盖的某种标准从而设计出新算法。
相对于机器学习其他分支来说，聚类的知识还不够系统化，因此著名教科书[Mitchell, 1997]中甚至没有关于聚类的章节。但聚类技术本身在现实任务中非常重要，因此本章勉强采用了“列举式”的叙述方式，相较于其他各章给出了更多的算法描述。关于聚类更多的内容，可参阅这方面的专门书籍和综述文章如[Jain and Dubes,1988; Jain et al., 1999; Xu and Wunsch II, 2005; Jain,2009]等。

　　聚类性能度量除9.2节的内容外，常见的还有F值、互信息(mutual information)、平均廊宽(average sihoouette width)[Rousseeuw,1987]等，可参阅[Jain and Dubes,1988; Halkidi et al., 2001; Maulik and Bandyopadhyay,2002].

　　距离计算是很多学习任务的核心技术。
闵可夫斯基距离提供了距离计算的一般形式。除闵可夫斯基距离之外，内积距离、余弦距离等也很常用，可参阅[Deza and Deza, 2009]。MinkovDM在[Zhou and Yu,2005]中正式给出。模式识别、图像检索等涉及负载语义的应用中常会涉及非度量距离[Jacob et al.,2000; Tan et al., 2009]。距离度量学习可直接嵌入到聚类学习过程中[Xing et al., 2003].

　　k均值算法可看作高斯混合聚类在混合成分方差相等、且每个样本仅指派给一个混合成分时的特例。该算法在历史上曾被不同领域的学着多次重新发明，如Steninhaus在1956年、Lloyd在1957年、McQueen在1967年等[Jain and Dubes, 1988; Jain, 2009]。
　　k均值算法有大量变体，如k-medoids算法[Kaufman and Rousseeuw, 1987]强制原型向量必为训练样本，k-modes算法[Huang, 1988]可处理离散属性，Fuzzy C-means(简称FCM)[Bezdek, 1981]则是“软聚类”(soft clustering)算法，允许每个样本以不同程度同时属于多个原型。
　　需要注意的是，k-均值类算法仅在凸形簇结构上效果较好。

　　最近研究表明，若采用某种Bregman距离，则可以显著增强此类算法对更多类型簇结构的适用性[Banerjee et al., 1988]，这与谱聚类(spectral clustering)[von Luxburg, 2007]有密切联系[Dhillon et al., 2004]，后者可看作在拉普拉斯特征映射(Laplacian Eigenmap)降维后执行k均值聚类。
　　聚类簇数k通常需由用户提供，有一些启发式用于自动确定k[Pellg and Moore, 2000; Tibshirani et al., 2001]，但常用的仍是基于不同k值多次运行后选取最佳结果。

　　LVQ算法在每轮迭代中仅更新与当前样本距离最近的原型向量。同时更新多个原型向量能显著提高收敛速度，相应的改进算法有LVQ2、LVQ3等[Kohonen, 2001].[McLachlan and Pee, 2000]详细介绍了高斯混合聚类，算法中EM迭代优化的推导过程可参阅[Bilmes, 1998; Jain and Dubes, 1988]。

　　采用不同方式表征样本分布的紧密程度，可设计出不同的密度聚类算法，除DBSCAN[Ester et al.,1996外，较常用的还有OPTICS[Ankerst et al.,1999]、DENCLUE[Hinneburg and keim, 1998]等。AGNES[Kaufman and Rousseeuw, 1990]采用了自底向上的聚合策略来产生层次聚类结构，与之相反的是，DIANA[Kaufman and Rousseeuw,1990]则是采用了自顶向下的分拆策略。AGNES和DIANA都不能对已合并或已分拆的聚类簇进行回溯调整，常用的层次聚类算法如BIRCH[Zhang et al.,1996]、ROCK[Guha et al., 1999]等对此进行了改进。

　　聚类集成(clustering ensemble)通过对多个聚类学习器进行集成，能有效降低聚类假设与真实聚类结构不符、聚类过程中的随机性等因素带来的不利影响，可参阅[Zhou, 2012]第7章。

　　异常检测(anomaly detection)[Hodge and Austin, 2004; Chandola et al., 2009]常借助聚类或距离计算进行，如将远离所有簇中心的样本作为异常点，或将密度极低处的样本作为异常点。最近有研究提出基于“隔离性”(isolation)可快速检测出异常点[Liu et al., 2012]。

参考材料:

[1] 周志华《机器学习》
[2] 李航《统计学习方法》
[3] 邱锡鹏《神经网络与深度学习》
[4] P, NP, NPC 和 NPhard

posted @ 2021-04-29 10:53 Xu_Lin 阅读(169) 评论(0) 编辑收藏举报

刷新页面返回顶部

Xu_Lin

Do more; Learn more; Be more

机器学习-聚类