蓝桥杯——不就是几个排序嘛!
一、前言
- 时间过得真的好快,转眼间看到自己第一篇关于蓝桥杯的文章,已经过了7天了
- 陆陆续续还好我在坚持
- 学习算法的路上并不容易,但是其实不枯燥,还好吧。😎
- 附上学算法人必备网站:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
二、排序
2.1 快速排序
2.1.1 快排之单向扫描分区法
- 虽然是单向扫描,但是我们仍然需要两个指针进行操作。
- 单向扫描,我们将左指针定义为主指针,以左指针为主进行的扫描。
- 当遇到左指针扫描的数比哨兵值大时,我们就将左右指针的数进行交换,将大的数换到后面,然后继续用左指针扫描。
public static int partition(int[] A, int l, int r) {
int pivot = A[l];
// 左侧扫描指针
int left = l + 1;
// 右侧指针
int right = r;
while(left <= right) {
// 扫描元素小于哨兵,左指针移动
if(A[left] <= pivot) {
left++;
}else {
// 扫描元素大于哨兵,则交换双指针指向的元素,将大的元素换到右边,右指针左移
Utils.swap(A,left,right);
right--;
}
}
Utils.swap(A,left,right);
return right;
}
2.1.2 快排之双向扫描分区法
- 双向扫描就是我们平时数据结构学习的正常快排算法
- 同样我们需要利用两个指针进行扫描
- 这里我使用两者快排写法,但是思想相同
写法一:
/**
* 快速排序一
* @param arr
* @param start
* @param end
* @return
*/
public static void quickSort(int[] arr, int start, int end) {
// 出口
if(start > end) return;
int low = start;
int high = end;
// 1.找哨兵
int temp = arr[start];
while(low < high) {
// 2.从最右侧开始扫描到比 哨兵 小的值,记录high
while(low < high && temp <= arr[high]) {
high--;
}
// 3.再从左侧扫描到比 哨兵 大的值,记录low
while(low < high && temp >= arr[low]) {
low++;
}
if(low < high) {
// 4.如果左指针仍然小于右指针,证明还没结束,将两个值交换位置
Utils.swap(arr, low,high);
}
}
// 5. 最后low小于high,low的位置是 小于哨兵中的最后一个元素,所以我们将low指针的值 和 哨兵的值进行交换。
// 交换后就达到了哨兵左侧的值小,右侧的值大
arr[start] = arr[low];
arr[low] = temp;
// 6.哨兵左侧继续排好序
quickSort(arr, start,low-1);
// 7.哨兵右侧继续排好序
quickSort(arr, low+1, end);
}
写法二:
/**
* 快速排序二:划分区域
* @param arr
* @param low
* @param high
* @return
*/
public static int partition(int[] arr, int low, int high) {
// 1.定义哨兵
int pivot = arr[low];
while(low < high) {
// 2.从右侧开始扫描,扫描到比哨兵小的值结束,记录high
while(low < high && arr[high] >= pivot) {
high--;
}
// 3. 将该值移动到左端,此时high位置空出
arr[low] = arr[high];
// 4.再从左侧开始扫描,扫描到比哨兵大的值结束,记录low
while(low < high && arr[low] <= pivot) {
low++;
}
// 5. 将该值移动到右端
arr[high] = arr[low];
}
// 6.最后将哨兵插入
arr[low] = pivot;
return low;
}
public static void quick_Sort(int[] arr, int low, int high) {
// 递归出口
if(low < high) {
int pivot = partition(arr, low, high);
quick_Sort(arr, low, pivot-1);
quick_Sort(arr, pivot+1, high);
}
}
- 在工业中,快排还是可以优化的,因为我们平时选择的哨兵都很随意,选择第一个元素。当哨兵选择的值尽量靠中间时,可以使我们的快排效率达到最大。
- 所以我们可以采取三点中值法进行选择哨兵
- 这是快排partition部分的代码,我们采用三点中值法选择哨兵。每次选哨兵时,不选最大也不选最小,而是选择中间大的元素。
public static int partition(int[] arr, int low, int high) {
// 三点中值法
// 中间下标
int midIndex = low + ((high - low) >> 1);
// 中间值下标
int midValueIndex = -1;
if(arr[low] <= arr[midIndex] && arr[low] >= arr[high]) { // 最右侧值 <= 第一个值 <= 中间值
midValueIndex = low;
}else if(arr[high] <= arr[midIndex] && arr[high] >= arr[low]) { // 最右侧值 <= 中间值
midValueIndex = high;
}else {
midValueIndex = midIndex;
}
// 1.定义哨兵
int pivot = arr[low];
while(low < high) {
// 2.从右侧开始扫描,扫描到比哨兵小的值结束,记录high
while(low < high && arr[high] >= pivot) {
high--;
}
// 3. 将该值移动到左端,此时high位置空出
arr[low] = arr[high];
// 4.再从左侧开始扫描,扫描到比哨兵大的值结束,记录low
while(low < high && arr[low] <= pivot) {
low++;
}
// 5. 将该值移动到右端
arr[high] = arr[low];
}
// 6.最后将哨兵插入
arr[low] = pivot;
return low;
}
2.2 归并排序
-
归并排序可以称为:分治模式的完美诠释
- 分解:将n个元素分成各个n/2个元素的子序列
- 解决:将两个子序列递归地排序
- 合并:合并两个已排序的子序列以得到排序结果
-
我们是通过递归的方式再次将n/2分解成n/2,一直分解到最小,不能再分解为止。然后进行合并。
与快排不同点:
- 归并的分解比较随意
- 归并的重点是合并
- 快排的重点是partition()函数,重点是划分
代码注意点:
- 最大的坑点就是,我们虽然单独开了一个数组,新开的数组值并且也复制了和原数组一样
- 但是每一次原数组的变化,我们的新开数组也要跟着变化,否则的话我们排序是失败的
/**
* 归并排序
* @param arr
* @param left
* @param right
*/
public static void mergeSort(int[] arr, int left, int right) {
helper = Arrays.copyOf(arr, arr.length);
// 4.递归出口
if(left < right) {
// 中间值
int mid = left + ((right - left) >> 1);
// 1.找重复、找变化:对中间值左半部分进行归并排序
mergeSort(arr, left, mid);
// 2.找重复、找变化:对中间值右半部分进行归并排序
mergeSort(arr, mid+1, right);
// 3.两个部分都排序后进行最重要的合并
merge(arr,left,mid,right);
}
}
/**
* 归并排序的合并
* @param arr
* @param l
* @param mid
* @param r
*/
public static void merge(int[] arr, int l, int mid, int r) {
// 指向原数组的指针
int current = l;
// 辅助数组的左指针
int left = l;
// 辅助数组的中间右指针
int right = mid + 1;
while(left <= mid && right <= r) {
if(helper[left] <= helper[right]) {
// 左右两边进行判断,将小的入数组
arr[current++] = helper[left++];
}else {
arr[current++] = helper[right++];
}
}
// 需要判断指针是否越界
while (left <= mid) {
// 当指针没越界,证明我们还没有合并完,所以将剩余的元素全部放入数组中
arr[current++] = helper[left++];
}
while (right <= r) {
arr[current++] = helper[right++];
}
}
public static void main(String[] args) {
int[] arr = {11,24,5,32,50,34,54,76};
mergeSort(arr, 0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
2.3 堆排序
用数组实现一颗二叉树,那么我们需要知道:
- 左节点:2*i+1
- 右结点:2*i+2
- 父节点:(i-1)/2
大根堆的构造:
- 大根堆就是根节点都大于其子节点的树
- 从最后一个非终端结点开始,从后往前进行调整
- 每次调整从上往下,将子节点比自己大的元素进行交换
- 调整为大根堆
排序思想:
- 构造完大根堆以后,整个数组最大值就是堆结构的顶端
- 将顶端的数与末尾的数交换,此时末尾的数为最大值,剩余待排序数组个数为n-1
- 将剩余的n-1个数,再次构造成大根堆,再将顶端的数与末尾的数交换
- 如此反复,就能得到一个升序的数组
// 1.大根堆——测试用例
public static void main(String[] args) {
int[] arr = {5,2,6,8,9,1,3,7};
heapMaxSort(arr,arr.length-1);
System.out.println(Arrays.toString(arr));
}
// 2.大根堆——排序调用
public static void heapMaxSort(int[] arr, int len) {
// 1. 先建立大根堆
buildMaxHeap(arr, len);
for (int i = len; i > 1; i--) {
// 2. 将堆顶元素与最后一个元素互换,最后一个变成了最大值
// 并且每一次交换都是交换的堆顶元素
Utils.swap(arr, 1,i );
// 3. 每一次调整都需要缩小范围
heapAdjustMax(arr, 1, i-1);
}
}
// 3.建立大根堆
public static void buildMaxHeap(int[] arr, int len) {
for (int i = len / 2; i > 0; i--) { // 从后往前调整所有非终端结点
heapAdjustMax(arr, i, len);
}
}
// 4.调整大根堆
// 将以K为根的子树调整为大根堆
public static void heapAdjustMax(int[] arr, int k, int len) {
// 将arr[0]暂存子树的根节点
arr[0] = arr[k];
for (int i = 2 * k; i <= len; i *= 2) { // 从根节点向下对子节点进行比较
if (i < len && arr[i] < arr[i + 1]) {
// 取key较大的子节点的下标
i++;
}
// 根节点和子节点中最大值进行比较,若根结点仍然是最大值,则无需调整。
if (arr[0] >= arr[i]) {
break;
} else {
// arr[i]比较大,所以将arr[i]调整到父节点上
arr[k] = arr[i];
k = i; // 修改k值,继续筛选
}
}
// 因为k是变化的,所以被筛选结点的值放入最终位置
arr[k] = arr[0];
}
2.4 计数排序
- 适用范围:序列关键字比较集中,已知边界,且边界较小
- 用辅助数组对数组中出现的数字计数,元素转下标,下标转元素
- 其实和哈希表差不多吧
- 开辟一个数组中最大元素值的空间,然后扫描标记
- 在顺序扫描新数组,将有标记的下标替代原数组即可
- 是一种排序效率的突破,但是空间换时间,所以适用于小范围数据
2.5 桶排序
通过“分配”和“收集”过程来实现排序
思想:设计k个桶(编号0~k-1),然后将输入n个数分布到各个桶中去,对各个桶中的数进行排序,然后按照次序把各个桶中的元素列出即可。
- 计数排序就很像我们的桶排序,只是计数排序的桶比较多、比较浪费。而桶排序的桶将很多数进行了分类,所以就节约了桶。
- 桶排序和散列表的链式结构非常像
- 适用于均匀分配的数据
- 后续文章会实现代码
2.6 基数排序
-
基于桶排序的一种排序算法
-
假设一组数据 73 22 93 43 55 14 28 65 39 81
-
我们按照个位数字放入桶中
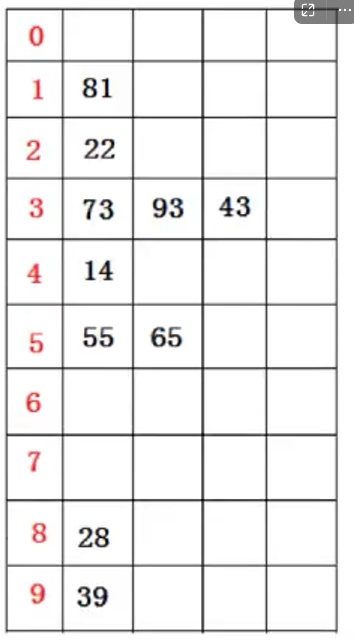
-
然后将数字拿出来 81 22 73 93 43 14 55 65 28 39
-
再次进行桶排序,根据十位数进行分配
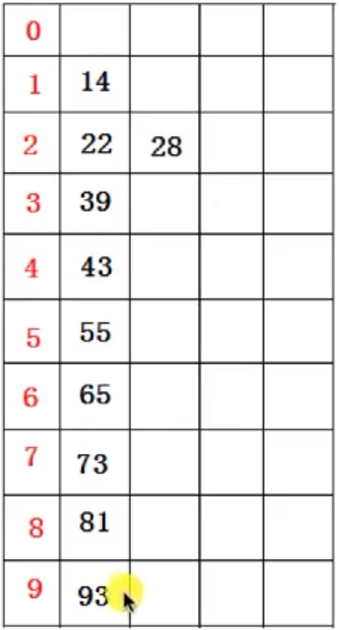
-
最后我们在收集桶里的数据,14 22 28 39 43 55 65 73 81 93
-
需要进行几轮进桶出桶,取决于最大数的位数
2.7 冒泡排序
- 谁大谁上,每一轮都把最大的顶到天花板
- 效率太低O(n^2)——掌握swap
// 简单优化:加一个flag进行判断,如果一趟没有交换过,那么就是有序的,直接结束排序即可
public static void bubbleSort(int[] arr) {
// 俩俩比较,所以外层比较 n-1次
for (int i = 0; i < arr.length-1; i++) {
// 优化标记
boolean flag = false;
// 内层比较,取决于i,因为外层比较过的最大值,无需进行继续比较,所以在外层的基础上-i
for (int j = 0; j < arr.length-i-1; j++) {
if(arr[j] > arr[j+1]) {
// 如果前一个数 > 后一个数,就进行交换
Utils.swap(arr, j, j+1);
flag = true;
}
}
if(flag) {
break;
}
}
}
2.8 选择排序
- 效率较低,经常用它内部循环方式来找最大值和最小值
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
// 最小值下标
int minIndex = i;
for (int j = i+1; j < arr.length; j++) {
// 用它依次与数组后面的值进行比较
if(arr[minIndex] > arr[j]) {
minIndex = j;
}
}
// 将记录的最小值下标与原记录进行交换
Utils.swap(arr,i,minIndex);
}
}
2.9 插入排序
- 虽然平均效率低,但是在序列基本有序时,效率较高
- 找到该数值,需要插入的位置,然后对数组进行移动,将该数插入进去即可。
- Arrays这个工具类在1.7里做了较大的改动
三、排序的实战练习
3.1 调整数组顺序,奇数在左、偶数在右
输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。要求时间复杂度为O()。
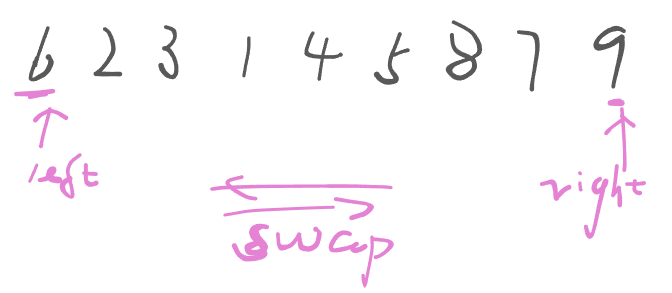
解法一:快排思想
- 左右双指针同时扫描,遇到奇数与偶数停止互换。
/**
* 奇数在左、偶数在右
*/
public static void johh(int[] arr) {
// 左指针
int left = 0;
// 右指针
int right = arr.length - 1;
while(left < right) {
// 如果左边扫描是奇数,则继续扫。扫到偶数停止,记录left
while(arr[left] % 2 != 0) {
left++;
}
// 如果右边扫描是偶数,则继续扫。扫到奇数停止,记录right
while(arr[right] % 2 == 0) {
right--;
}
if(left <= right) {
Utils.swap(arr, left, right);
}
}
}
解法二:归并思想
- 再开一个数组,仍然是双指针
- 左右扫描,扫到奇数就放前面,扫到偶数就放后面
- 但是这种方法很明显多开了个O(n)的空间
3.2 第k个元素
以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值
算法思想:
-
这道题的算法应用我们分区的思想
-
当我们用快排的分区时,我们哨兵的位置 就是他实际排序的下标,哨兵左侧都是小的值,右侧都是大的值
-
此时我们在进行比较哨兵的位置,是否是我们要找的K位置。
-
如果 K小于哨兵的位置,我们就进行左侧寻找,对左侧进行划分
-
如果 K大于哨兵的位置,我们就进行右侧寻找,对右侧进行划分
-
直到我们找到K的位置为止
-
-
容易出错的地方就是我们下标的确定
/**
* 第k个元素
* @param arr 数组
* @param left 左指针
* @param right 右指针
* @param indexK 找K个元素。第2个元素,在数组中实际上是arr[1]
*/
public static int selectK(int[] arr, int left, int right, int indexK) {
// 拿到分区的中间下标,此值的位置就是排序后的位置
int index = 快排.partition(arr, left,right);
// 哨兵实际的位置
int realIndex = index - left + 1;
if(realIndex == indexK) { // 如果说分区的实际位置==我们要找的元素位置
return arr[index];
}else if(indexK < realIndex) { // 如果我们找的元素位置 < 分区下标位置,则去左侧继续分区寻找
return selectK(arr, left,index-1,indexK);
}else {
// indexK-realIndex 如果在右侧,则递归后范围变小了,所以要减去前面的realIndex
return selectK(arr, index+1, right, indexK-realIndex);
}
}
public static int partition(int[] arr, int low, int high) {
// 三点中值法
// 中间下标
int midIndex = low + ((high - low) >> 1);
// 中间值下标
int midValueIndex = -1;
if(arr[low] <= arr[midIndex] && arr[low] >= arr[high]) { // 最右侧值 <= 第一个值 <= 中间值
midValueIndex = low;
}else if(arr[high] <= arr[midIndex] && arr[high] >= arr[low]) { // 最右侧值 <= 中间值
midValueIndex = high;
}else {
midValueIndex = midIndex;
}
// 1.定义哨兵
int pivot = arr[low];
while(low < high) {
// 2.从右侧开始扫描,扫描到比哨兵小的值结束,记录high
while(low < high && arr[high] >= pivot) {
high--;
}
// 3. 将该值移动到左端,此时high位置空出
arr[low] = arr[high];
// 4.再从左侧开始扫描,扫描到比哨兵大的值结束,记录low
while(low < high && arr[low] <= pivot) {
low++;
}
// 5. 将该值移动到右端
arr[high] = arr[low];
}
// 6.最后将哨兵插入
arr[low] = pivot;
return low;
}
3.3 寻找发帖水王
Tngo是微软亚洲研究院的一个试验项目。研究院的员工和实习生们都很喜欢在Tango上面交流灌水。传说,Tango有一大“水王”,他不但喜欢发贴,还会回复其他D发的每个帖子。坊间风闻该“水王”发帖数目超过了帖子总数的一半。如果你有一个当前论坛上所有帖子(包括回帖)的列表,其中帖子作者的D也在表中,你能快速找出这个传说中的Tango水王吗?
算法思想:消除法
- 因为题中说了数量超过了数组的一半,就意味着即使两个不同的数字互相消除,那么最后剩下的一个数仍然是我们要找的数字。
- 消除的数字出现次数改为0,所以他出现的次数最少为1次。
/**
* 不同的数,两两消除
* @param arr
*/
public static void searchW(int[] arr) {
// 候选下标
int calIndex = 0;
// 出现次数
int times = 1;
for (int i = 1; i < arr.length-1; i++) {
if(times == 0) {
// 如果消除后,我们应该更新候选值
calIndex = i;
times = 1;
continue;
}
// 如果两者相等,则次数加1
if(arr[calIndex] == arr[i]) {
times++;
}else {
times--;
}
}
// 最后剩下的元素次数一定大于等于1,就是我们的候选值
System.out.println(arr[calIndex]);
}
3.4 最小可用ID
在非负数组(乱序)中找到最小的可分配的id(从1开始编号),数据量1000000
/**
* 解法一:快排 复杂度O(nLog(n))
* @param arr
*/
public static void searchMinId(int[] arr) {
快排.quick_Sort(arr, 0, arr.length-1);
int i = 0;
while(true) {
if(arr[i] == i+1) {
i++;
continue;
}
System.out.println(i+1);
break;
}
}
解法二:O(n)
- 开辟一个空间,依次比较将数组中的数标记到新数组中1。
- 最后扫描一遍新数组,找到值为0的就是我们要找的值。
- 但是如果数据量较大,那么我们开辟的空间也将非常大。
public static void searchMinIdTwo(int[] arr) {
int[] helper = new int[arr.length+1];
for (int i = 0; i < arr.length; i++) {
// 我们排好序后的数字肯定会小于他的长度,如果突然来个10000,那么前面不会最大值只为10
// 如果最大值只为10,那么我们就可以忽略掉10000
// 缺少的部分肯定在0——10之间
if(arr[i] < arr.length+1)
helper[arr[i]]++;
}
for (int i = 1; i < helper.length; i++) {
if(helper[i] < 1) {
System.out.println(i);
break;
}
}
}
解法三:利用快排思想的partition()
- 大家自行研究吧~~~😶🌫️
3.5 合并有序数组
给定两个排序后的数组A和B,其中A的末端有足够的缓冲空间容纳B。编写一个方法,将B合并入A并排序
算法思想:
- 与归并排序的思想很像,将两个数组合并成一个有序的数组
- 同时使用三个指针进行操作
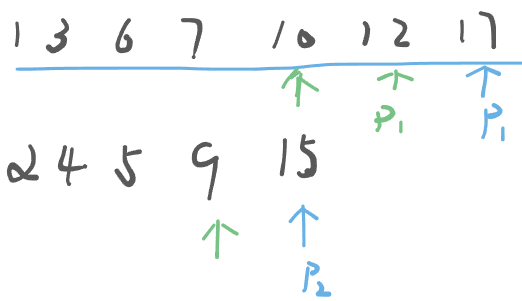
public class 合并有序数组 {
public static void main(String[] args) {
int[] arr1 = {1,3,6,7,10,12,17};
int[] arr2 = new int[12];
arr2[0] = 2;
arr2[1] = 4;
arr2[2] = 5;
arr2[3] = 9;
arr2[4] = 15;
mergeArr(arr1, arr2);
Utils.printf(arr2);
}
// 获取数组元素个数
public static int getElementCount(int[] arr) {
int count = 0;
for (int i = 0; i < arr.length; i++) {
if(arr[i] != 0) {
count++;
}
}
return count;
}
// 我们要将arr1的数,放入扩容的arr2中
public static void mergeArr(int[] arr1, int[] arr2) {
// 指向arr2数组末尾的指针,用来移动
int current = arr2.length - 1;
// 指向arr1数组末尾的指针
int p1 = arr1.length-1;
// 指向arr2最后一个元素的指针
int p2 = getElementCount(arr2) - 1;
// arr1数组元素全部放到arr2中为止
while(p1 != -1) {
while(arr1[p1] > arr2[p2]) {
arr2[current--] = arr1[p1--];
}
while(p2 != -1 && arr1[p1] <= arr2[p2]) {
arr2[current--] = arr2[p2--];
}
// 需要单独考虑如果arr2的元素个数比arr1少,那么p2很可能快速到达0
while(p2 == -1 && p1 != -1) {
arr2[current--] = arr1[p1--];
}
}
}
}
3.6 逆序对个数
一个数列,如果左边的数大,右边的数小,则称这两个数位一个逆序对。求出一个数列中有多少个逆序对。
算法思想:
- 通过归并排序将左右两侧都变成有序,我们根据右侧进行判断
- 如果右侧比左侧数小,那么就是逆序,逆序的个数就是左侧剩余数的个数
- 归并排序通过递归已经将元素进行就拆分,当我们无法继续拆分的时候,肯定执行当前的函数,所以就进行了合并,然后再从小问题合并成最后大的问题,最后就解决了。
- 这也是非常经典的分治思想
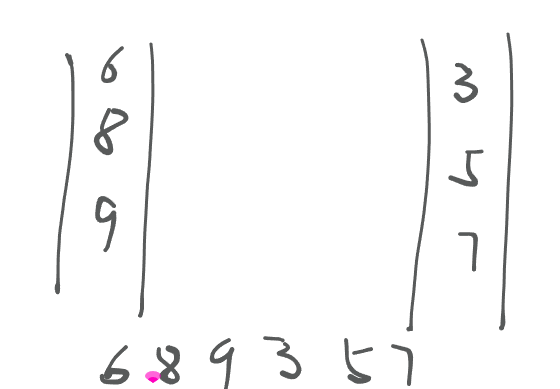
public static void merge(int[] arr, int l, int mid, int r) {
// 记录逆序数
int count = 0;
// 指向原数组的指针
int current = l;
// 辅助数组的左指针
int left = l;
// 辅助数组的中间右指针
int right = mid + 1;
while(left <= mid && right <= r) {
if(helper[left] <= helper[right]) {
arr[current++] = helper[left++];
}else {
arr[current++] = helper[right++];
count += mid - left + 1;
}
}
while (left <= mid) {
arr[current++] = helper[left++];
}
while (right <= r) {
arr[current++] = helper[right++];
}
}
public static void mergeSort(int[] arr, int left, int right) {
helper = Arrays.copyOf(arr, arr.length);
// 4.递归出口
if(left < right) {
// 中间值
int mid = left + ((right - left) >> 1);
// 1.找重复、找变化:对中间值左半部分进行归并排序
mergeSort(arr, left, mid);
// 2.找重复、找变化:对中间值右半部分进行归并排序
mergeSort(arr, mid+1, right);
// 3.两个部分都排序后进行最重要的合并
merge(arr,left,mid,right);
}
}
3.7 排序数组中找和的因子
给定已排序数组arr和k,不重复打印arr中所有相加和为k的不降序二元组如
输入arr={-8,-4,-3,0,2,4,5,8,9,10},k=10
输出(0,10)(2,8)
- 经典双指针扫描思想
public static void selectSum(int[] arr, int k) {
int left = 0;
int right = arr.length - 1;
while(left <= right) {
// 如果左侧扫描值仍然小于k,则继续向右扫描。因为数组是递增的
while (arr[left] + arr[right] < k) {
left++;
}
// 如果右侧扫描值仍然大于k,则继续向左扫描。因为数组是递增的
while(arr[left] + arr[right] > k) {
right--;
}
// 最后判断我们两个指针位置的数是否等于k,如果等于k,则继续移动一个指针,让扫描继续下去
if(arr[left] + arr[right] == k && left < right) {
System.out.println("("+arr[left]+","+arr[right]+")");
left++;
}
}
}
3.8 前K个数
求海量数据(正整数)按逆序排列的前k个数(topK),因为数据量太大,不能全部存储在内存中,只能一个一个地从磁盘或者网络上读取数据,请设计一个高效的算法来解决这个问题
不限制用户输入数据个数,用户每输入一个数据就回车使得程序可立即获得这个数据,用户输入-1代表输入终止
然后用户输入K,代表要求得topK
请输出topK,从小到大,空格分割
解法一:
- 在已有数据中维持一个最小值,当我们有新的数据要进入时,与最小值进行比较
- 如果新的数据比我们的最小值大,那么就让他进入我们的数组中
- 如果没有最小值大,则没有进入数组的资格
- 然后逆序输出我们的数组即可
- 但是我们这个并没有进行排序,所以时间复杂度是O(n)
public class 前k个数 {
public static int[] arr;
public static int size;
public static int k;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
k = scan.nextInt();
arr = new int[k];
int x = 0;
while(x != -1) {
x = scan.nextInt();
sout(x);
}
}
public static void sout(int x) {
// 数组元素个数为达到k个,直接插入
if(size < k) {
arr[size++] = x;
}else if(size == k) {
// 达到k个后,进行判断
int min = selectMin(arr);
if(x > min) {
arr[0] = x;
}
Utils.printf(arr);
}
}
/**
* 寻找数组中的最小值
* @param arr
* @return
*/
public static int selectMin(int[] arr) {
int min = 99999;
int index = -1;
for (int i = 0; i < arr.length; i++) {
if(min > arr[i]) {
min = arr[i];
index = i;
}
}
// 将我们的最小值换到第一个位置
Utils.swap(arr,index,0);
return min;
}
}
解法二:
- 使用小顶堆可以将复杂度优化到O(nLg(n))
- 我们维持一个小顶堆,每一次都用根结点(最小值)进行比较
- 当有新的值加入后,我们继续进行小顶堆调节,将最小值调节到根节点,反复如此
3.9 所有员工年龄排序
公司现在要对几万员工的年龄进行排序,因为公司员工的人数非常多,所以要求排序算法的效率要非常高,你能写出这样的程序吗
- 输入:输入可能包含多个测试样例,对于每个测试案例
- 输入的第一行为一个整数n(1<=n<=1000000):代表公司内员工的人数。
- 输入的第二行包括个整数:代表公司内每个员工的年龄。其中,员工年龄
- age的取值范围为(1<=age<=99)。
- 输出:对应每个测试案例
- 请输出排序后的n个员工的年龄,每个年龄后面有一个空格。
- 采用计数排序解决问题,时间复杂度O(n)
public class 所有员工年龄排序 {
public static int[] arr;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
arr = new int[100];
while(n != 0) {
int age = scan.nextInt();
arr[age]++;
n--;
}
for (int i = 0; i < arr.length; i++) {
while(arr[i] != 0) {
System.out.println(i);
arr[i]--;
}
}
}
}
3.10 特殊排序
输入一个正整数数组,把数组里所有整数拼接起来排成一个数,打印出能拼接出的所有数字中最小的一个。
例如输入数组{3,32,321},则打印出这3个数字能排成的最小数字为:321323
- 我们可以自定义排序的规则
public static int f(Integer[] arr) {
// 通过匿名内部类,自定义比较规则
Arrays.sort(arr,new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
String s1 = o1 + "" + o2;
String s2 = o2 + "" + o1;
return s1.compareTo(s2);
}
});
StringBuilder sb = new StringBuilder();
for (int i = 0; i < arr.length; i++) {
sb.append(arr[i]);
}
return Integer.parseInt(sb.toString());
}
3.11 判断数组的包含问题
输入两个字符串str1和str2,请判断str1中的所有字符是否都存在与str2中
- 学会合理使用Java的API类库
解法一:利用api判断
public static boolean isInclude(String s1, String s2) {
for (int i = 0; i < s1.length(); i++) {
// 取出s1串中的字符
char c = s1.charAt(i);
// 通过api判断是否s2字符串是否包含c
if(s2.indexOf(c) == -1) {
return false;
}
}
return true;
}
解法二:快排 + 二分查找
public static boolean isIncludes(String s1, String s2) {
// 将s2字符串转成字符数组
char[] s2Arr = s2.toCharArray();
// 变成数组的目的就是为了快排后二分查找
Arrays.sort(s2Arr);
for (int i = 0; i < s1.length(); i++) {
char c = s1.charAt(i);
if(Arrays.binarySearch(s2Arr, c) == -1) {
return false;
}
}
return true;
}
四、结尾
- 对于蓝桥杯排序知识内容就总结这么多,若想深入学习等待后续更新。
- 我将会继续更新关于蓝桥杯方向的学习知识,感兴趣的小伙伴可以关注一下。
- 文章写得比较走心,用了很长时间,绝对不是copy过来的!
- 尊重每一位学习知识的人,同时也尊重每一位分享知识的人。
- 😎你的点赞与关注,是我努力前行的无限动力。🤩


