蓝桥杯——查找的妙趣
一、查找
1.1 递归式二分查找
- 作为查找的必学算法,二分查找大家一定不陌生,通过前面我们所学的递归,那么我们继续强化递归思想,将二分查找转换成递归的方式。
- 任何循环都能改成递归,递归也可以改成任何循环。
算法思想:
- 全范围内二分查找
-
等价于三个子问题
-
左边找(递归):缩小范围,可用递归,并且重复
-
中间比
-
右边找(递归):缩小范围,可用递归,并且重复
-
-
注意:
-
左查找和右查找只选其中一个
-
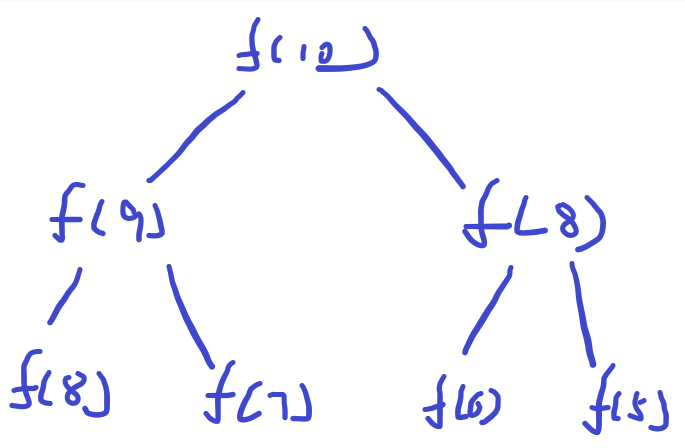
递归如果画图就会发现,其实是一个类似树的样子,有线性的,有二分的,三分的...
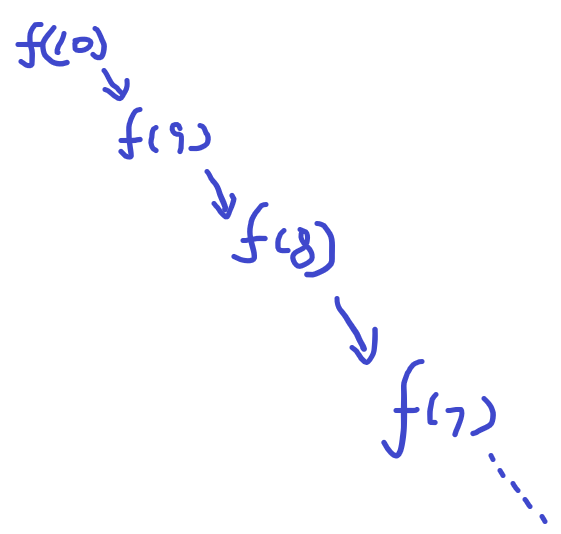
-
二分查找就像下面这样,但是每一次都会舍去一半,这也是二分查找效率高的原因
/**
* 递归式二分查找
* @param arr 数组
* @param low 左指针
* @param high 右指针
* @param value 查找值
* @return
*/
public static int binarySearch(int[] arr, int low, int high, int value) {
// 递归三步走:3. 找出口
if(low > high) return -1;
int mid = low + (high - low)/2;
if(value < arr[mid]) {
// 找重复、找变化:对左半部分进行二分查找,最后返回的是我们查找的结果
return binarySearch(arr,low, mid-1, value);
}
else if(value > arr[mid]) {
// 找重复、找变化:对右半部分进行二分查找,最后返回的是我们查找的结果
return binarySearch(arr,mid+1, high, value);
}
else return mid;
}
1.2 旋转数组最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1.
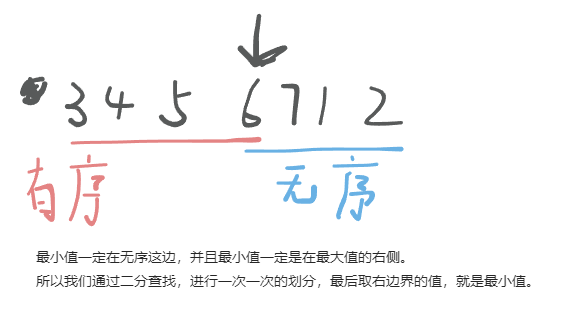
- 最小值一定在无序的那边,并且在最大值的右侧,因为我们题中给的就是有序递增序列。
- 看到有序递增序列的字眼,我们直接就能想到二分查找。
- 此题也是二分查找的一种变形
public static int ef(int[] arr) {
int low = 0;
int high = arr.length - 1;
// 没有翻转的情况
if(arr[low] < arr[high]) return arr[low];
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (arr[mid] >= arr[low]) {
// 中间值大于左边开始元素,则左边是有序的,最小值一定藏在右边
low = mid;
} else {
high = mid;
}
}
// 因为最小值一定在右侧
return arr[high];
}
1.3 在有空字符串中的有序字符串查找
有个排序后的字符串数组,其中散布着一些空字符串,编写一个方法,找出给定字符串(肯定不是空字符串)的索引。
- 这个题就不画图了,非常简单,就是当我们中间mid取到空字符串时候,我们移动mid指针,直到不指向空为止。
public static int indexOf(String[] arr, String p) {
int begin = 0;
int end = arr.length - 1;
while(begin <= end) {
int mid = begin + ((end - begin) >> 1);
while(arr[mid].equals("")) {
mid++;
}
if(arr[mid].compareTo(p) > 0) {
end = mid - 1;
}else if(arr[mid].compareTo(p) < 0) {
begin = mid + 1;
}else {
return mid;
}
}
return -1;
}
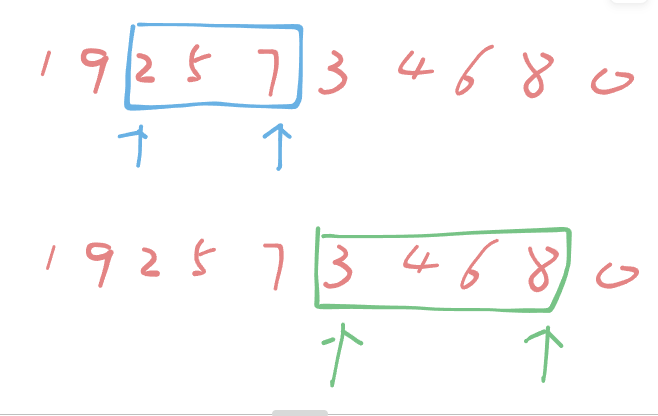
1.4 找出最长连续递增子序列
(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)
- 这个题非常的经典,我们可以采用双指针策略,也称之为滑动窗口算法。
- 模拟一个窗口进行滑动,最后窗口内的区域就是我们想要的答案。
public static int zczxl(int[] arr) {
// 用于存放结果
int temp = 0;
for (int i = 0; i < arr.length; i++) {
// 滑动窗口右指针
int right = i+1;
int count = 0;
// 1.当右指针扫描到最后 或者 符合递增条件时
while(right < arr.length && arr[right] > arr[i]) {
// 2.符合条件,我们让右指针继续移动,扩大我们的窗口,直到移动到不符合条件为止
right++;
i++;
count++;
}
// 3.更新结果,取最优解,也是最大值。
temp = temp < count+1 ? count+1 : temp;
// 4.我们通过更新i,也就是刷新了左指针,让左侧窗口右移
}
return temp;
}
二、 梦回递归
2.1 小白上楼梯
小白正在上楼梯,楼梯有n阶台阶,小白一次可以上1阶,2阶或者3阶,实现一个方法,计算小白有多少种走完楼梯的方式。
-
我们仍然再练习其它算法的同时,不忘记我们的递归训练。
-
和斐波那契数列很相似,不过变成了递归三分支的
-
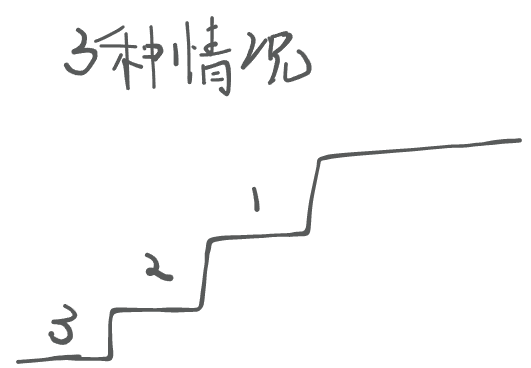
我们通过逆推的方式,可以判断最后上台阶只有三种模式,一种是差一步、第二种差两个台阶、第三种差三个台阶
-
将这三种情况子问题我们通过递归求出后,汇总即可。
public static int slt(int n) {
// 3. 找出口
if(n == 0) return 0;
if(n == 1) return 1;
if(n == 2) return 2;
if(n == 3) return 4;
// 1.找重复
// 2.找变化
return slt(n-1) + slt(n-2) + slt(n-3);
}
2.2 设计一个高效的求a的n次幂的算法
解法一:O(n)
- 这种解法正常人都能想出来
/**
* a的n次幂
* @param a
* @param n
* @return
*/
public static int pow1(int a, int n) {
int res = 1;
for (int i = 0; i < n; i++) {
res *= a;
}
return res;
}
解法二:
既然解法一是O(n),那么我们如果想要再次优化算法的时间,必然是logN级别的
- 81 = 3^2 * 3^2 = 3^4
- 所以我们先通过阶乘求其一部分值,最后通过递归解决另一部分值,让二者相乘就是我们的答案!
- 还是非常的应用了:递归自己干一部分,另一部分交给别人的思想!
public static int pow(int a, int n) {
int res = a;
int ex = 1;
if(n == 0) return 1;
// 通过阶层,我们先进行乘一部分
while((ex<<1) <= n) {
res *= res;
ex <<= 1;
}
return res * pow(a,n-ex);
}
三、结尾
- 对于蓝桥杯查找知识内容就总结这么多,若想深入学习等待后续更新。
- 我将会继续更新关于蓝桥杯方向的学习知识,感兴趣的小伙伴可以关注一下。
- 文章写得比较走心,用了很长时间,绝对不是copy过来的!
- 尊重每一位学习知识的人,同时也尊重每一位分享知识的人。
- 😎你的点赞与关注,是我努力前行的无限动力。🤩


