正则化及其稀疏性解释
（如下为搬运）本文翻译自：L1 Norm Regularization and Sparsity Explained for Dummies
0. 前言
好吧，我想我就是很笨的那一类人。 当理解一个抽象的数学概念，我必须把它转化成一张图像，然后在脑海中看到并触摸它。 我需要几何、物体、想法背后的直觉，以及现实生活中生动的比喻才能更好的去理解它。
当我发现人们不用这种方式思考或解释问题，只是指着方程式和论文对我说:"没有简单的解释"时，我就很生气。 通常在我仔细考虑之后，我可以找到这些想法简单、直观的解释。 就在昨天，当我试图理解应用于机器学习的L1 范数正则化为什么能保证稀疏性时，就有这样的一个经历。 因此，我想写这样一个博客来直观的阐述其背后的原理。
在小数据集上训练时，经常会碰到过拟合的问题，模型准确地记住了所有训练数据，包括噪声和不相关的特征。 这样的模型通常在新的测试集或之前从未见过的真实数据上表现不佳。 由于模型过于认真地对待训练数据，它没有从中学到任何有意义的模式，而只是记住了它所看到的一切，基本没有任何泛化能力。
现在，解决此问题的一种方案称为正则化。 这个想法是将 L1 范数应用到机器学习问题的解向量（在深度学习的情况下，它是神经网络权重）中，并试图使其尽可能小。 因此，如果你的初始目标是找到最佳向量 x 以及最小化损失函数 f(x)，那么您的新任务应该将 x 的 L1 范数加入到损失函数中(f(x) + L1-norm(x))，并找到最小值 。
很多人经常跟你讲：加入 L1 范数后往往可以得到稀疏解。 稀疏意味着解向量 x 的大部分分量（权重）为零，只有少数是非零的。 而稀疏的解决方案可以避免过度拟合。 就是这样，这就是他们在大多数文章、教科书、材料中的一笔带过的解释方式。 不加解释地提出一个想法就像在我的脑后推一把长矛。
不知道你们怎么想的，但通过 L1 范数来确保稀疏性从而避免过拟合对我来说并不是那么的显而易见。 我花了一些时间才弄清楚原因。 总体上，我有以下几个问题：
- 什么是过拟合？
- 为什么稀疏解决方案可以避免过拟合？
- 为什么在损失函数中加入 L1 范数会给出稀疏解？
- 正则化的真正作用是什么？
1. 什么是过拟合？
我最初的困惑来自这样一个事实，即我只看 L1 范数（忽略损失函数），只考虑 L1 范数很小意味着什么。 然而，我真正应该做的是将损失函数和 L1 范数惩罚作为一个整体来考虑。
我想用一个具体的例子从头开始解释过拟合问题。 假设你购买了一个机器人，并想通过查看以下示例来教他对汉字进行分类：
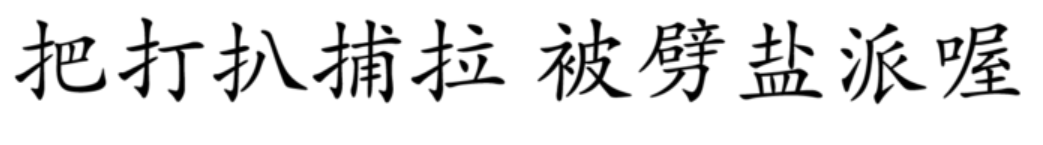
前5个汉字属于第一类，后5个汉字属于第二类。 而这 10 个汉字是你目前拥有的唯一训练数据。
然而，这个分类任务来说对机器人来说太简单了。 它有足够大的内存来记住 5 个汉字。 在看到所有 10 个汉字后，机器人学会了一种对它们进行分类的方法：它准确地记住了前 5 个汉字。 只要汉字不是这 5 个中的一个，机器人就会将该汉字归入第二类。 当然，这种方法在 10 个训练汉字上效果很好，因为机器人可以达到 100% 的准确率。 但是，当你提供了一个新汉字：
这个汉字本应该属于第一类（因为都有相同的偏旁）。 但是因为它从未出现在训练数据中，所以机器人之前没有见过它。 根据其算法，机器人会将这个汉字归入第二类，但很显然这是错误的。
我们人类应该很明显看到这里的模式。 所有属于第一类的汉字都有一个共同的偏旁（提手旁）。 但机器人未能完成这个任务，因为它太聪明了（聪明反被聪明误），而且训练数据太小。
这就是过拟合的问题。 但是什么是正则化，为什么稀疏可以避免过拟合？
2. 什么是正则化，为什么稀疏可以避免过拟合？
现在假设你对你的机器人生气了。你用锤子敲打机器人的头部，一边敲击，一边从他的头上甩下它的一些记忆芯片。你基本上已经让机器人变得更笨了。现在，机器人不能记住 5 个汉字，而只能记住一个字符部分。
你让机器人通过查看所有 10 个汉字再次进行训练，并仍然强迫他达到相同的准确度。因为这次他不能记住所有 5 个汉字，所以他得寻找更简单的模式。现在他发现了所有A类汉字的共同点！
这正是 L1 范数正则化所做的。它撞击你的机器人（模型）以使其“变笨”。因此，它必须从数据中寻找更简单的模式，而不是简单地记住东西。以机器人为例，当他能记住5个汉字时，他的“大脑”有一个大小为 5 的向量：[把、打、扒、捕、拉]。现在经过正则化后，他的4个内存槽无法使用（被正则化敲坏了）。因此新学习到的向量是：[扌, 0, 0, 0, 0]，很明显，这是一个稀疏向量。
更正式地说，当您使用较少的训练数据求解大向量 x 时。 x 的解可能有很多。
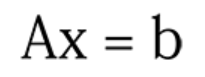
这里 A 是一个包含所有训练数据的矩阵。 x 是您正在寻找的解向量。 b 是标签向量。
当数据不够多并且你的模型参数很多时，你的矩阵 A 将不够“高”，你的 x 很长。 所以上面的等式看起来像这样
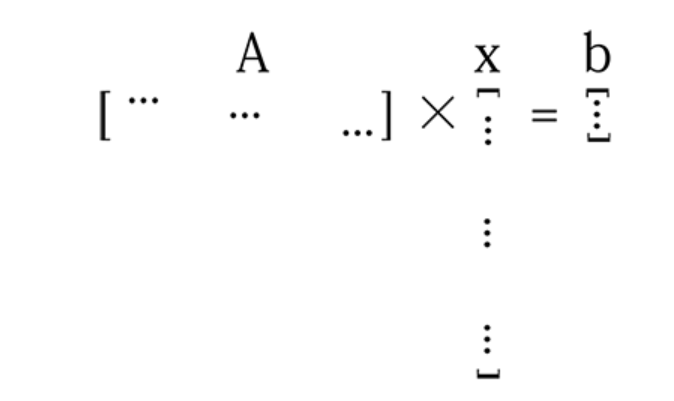
对于这样的线性方程组（欠约束），x可能有无穷解。要从这些解决方案中找到一个好的解，您需要确保所选解x 的每个分量（列向量的每一个值）都捕获了数据的有用特征。通过 L1 正则化，你本质上使向量 x 更小（稀疏），因为它的大部分分量都是无用的0，同时，剩余的非零分量将会非常“有用”。
我能想到的另一个比喻是这样的：假设你是一个人口众多、总体GDP还可以的王国的国王，但人均GDP很低。你的一些公民都很懒惰，没有生产力，因此你很生气。你命令国民：“提高生产力、变得强壮、勤奋，否则你会死！”，结果，许多人因你的严厉制度而死去，而那些真正能干、有生产力的人在你的暴政下幸存下来。你可以认为这里的人口是你的解向量 x 的大小，并且命令人们生产或死亡本质上是正则化。在正则化稀疏解中，您确保向量 x 的每个分量都非常有能力。每个分量都必须捕获一些有用的数据特征或模式。
深度学习中的另一种正则化方法是dropout。这个想法很简单，在训练时从神经网络中移除一些随机的神经连接，一段时间后再添加回来。从本质上讲，这仍然是试图通过减小神经网络的大小来使您的模型“变笨”，并对剩余的权重施加更多的责任和压力，以学习一些有用的东西。一旦这些权重学习了良好的特征，然后再添加其他连接以接受新数据。在上面的比喻中，我想把这种添加回连接的事情看作是“当你的人手不足时，将移民引入你的王国”。
基于这种“让模型变得更笨”的想法，我想我们可以想出其他类似的方法来避免过度拟合，比如从一个小网络开始，当有更多数据可用时逐渐向网络添加新的神经元和连接。或者在训练时执行修剪以摆脱接近于零的连接。
到目前为止，我们已经证明了为什么稀疏可以避免过度拟合。但是为什么在损失函数中添加一个 L1 范数并迫使解的 L1 范数变小会产生稀疏性呢？
3. 为什么在损失函数中加入 L1 范数会给出稀疏解？
昨天当我第一次想到这个时，我使用了两个示例向量 [0.1, 0.1] 和 [1000, 0]。第一个向量显然不是稀疏的，但它的 L1 范数较小。这就是我感到困惑的原因，因为仅查看 L1 范数并不能理解这个想法。我必须将整个损失函数作为一个整体来考虑。
让我们回到Ax=b的问题，举一个简单具体的例子。假设我们想找到一条直线拟合2D 空间中的一组点。我们都知道你至少需要 2 个点才能确定一条直线。但是如果训练数据只有一个点呢？那么你将有无限的解：每条通过点的直线都是一个解。假设这个点在[10, 5]处，我们可以定义一条直线:y = a * x + b。 那么问题就是确定这里的a和b。
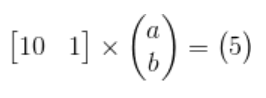
将[10,5]代入y = a*x + b，我们得到 b = 5 – 10 * a，那么下面这条线上的所有点 b = 5 – 10 * a 应该是一个解：
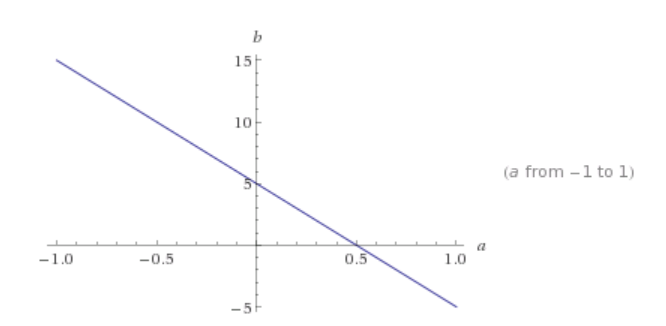
但是如何找到具有 L1 范数的稀疏解呢？
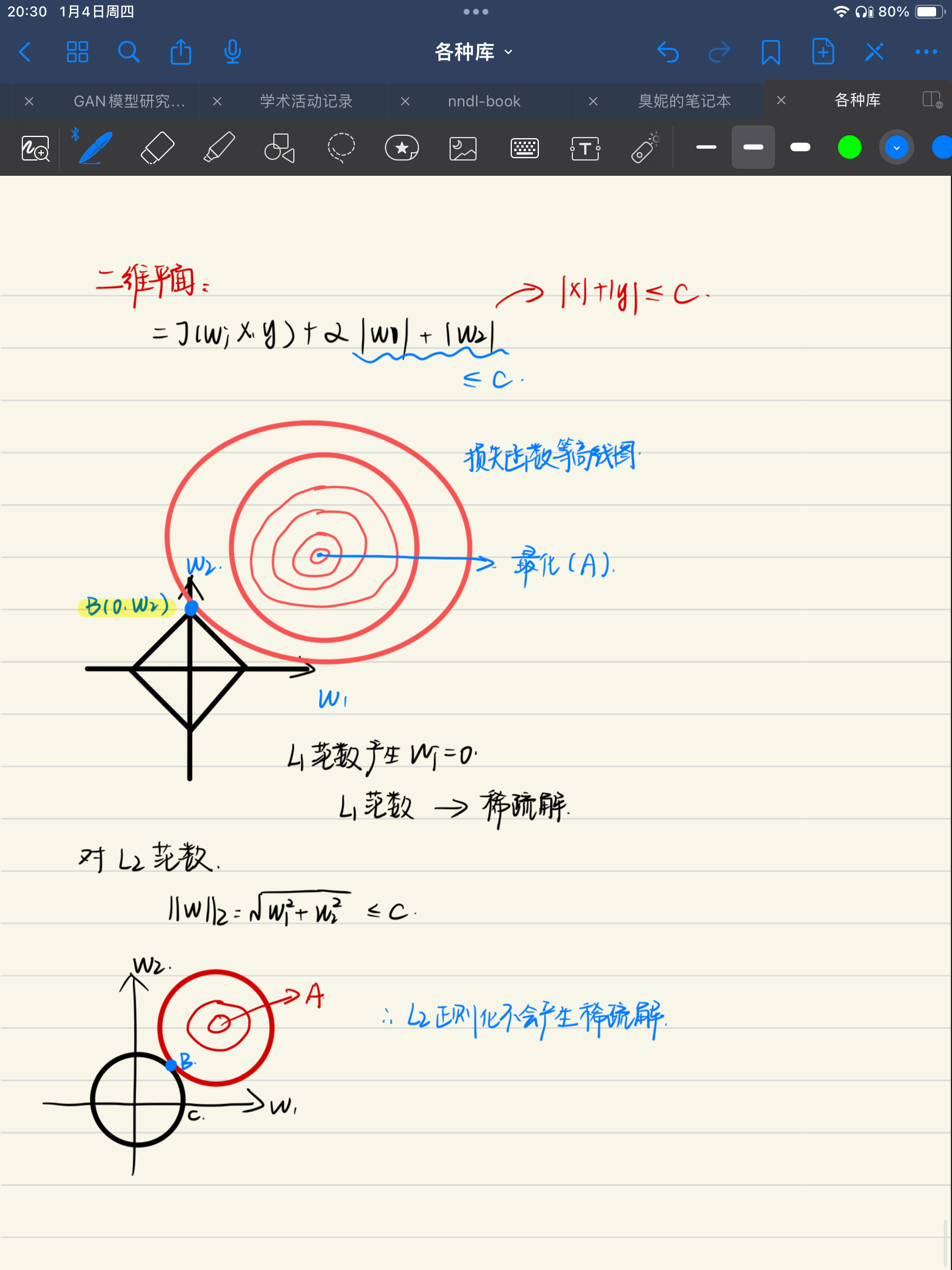
L1 范数定义为向量中所有分量的绝对值之和。 例如，如果一个向量是 [x, y]，它的 L1 范数是 |x| + |y|。
现在，如果我们绘制所有 L1 范数等于常数 c 的点，这些点应该形成如下所示的东西（红色）：
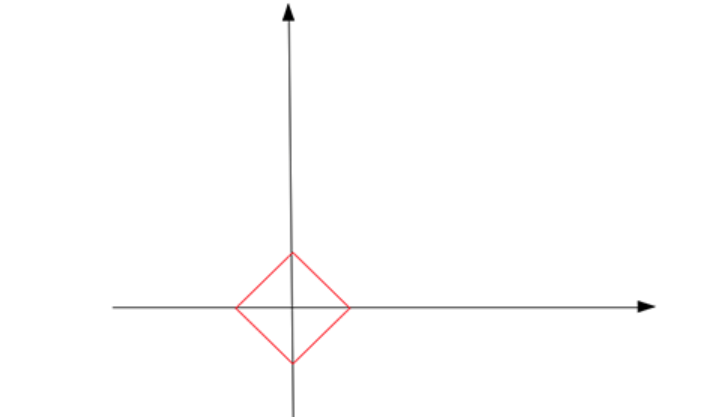
这个形状看起来像一个倾斜的正方形。 在三维空间中，它将是一个八面体(更高维空间类推)。 请注意，在此红色形状上，并非所有点都是稀疏的。 仅在尖端顶点上是稀疏的。 也就是说，一个点的 x 或 y 分量为零。 现在，找到稀疏解的方法是通过给出一个不断增长的 c (|x| + |y| = c)来“接触”蓝色解线，从原点放大这个红色形状。 直觉是接触点最有可能位于形状的尖端。 由于尖端是一个稀疏点，接触点定义的解也是一个稀疏解。
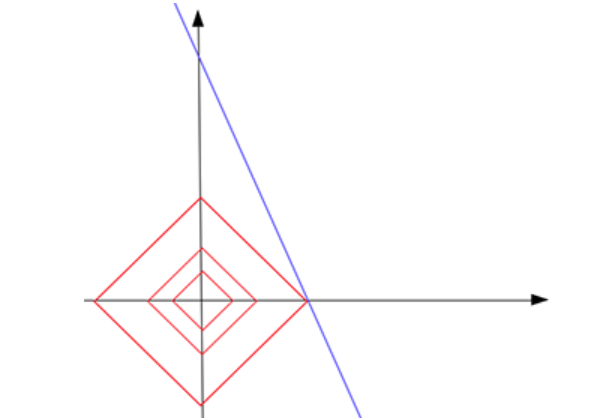
例如，在此图中，红色形状增长了3次（|a|+|b| = 0.5），直到它触及蓝线 b = 5–10 * a。如您所见，触点位于红色形状的尖端。接触点 [0.5, 0] 是一个稀疏向量。因此，我们说，通过从所有可能的解（蓝线上的点）中找到具有最小 L1 范数 (0.5) 的解点，我们找到了问题的稀疏解 [0.5, 0]。在接触点，常数 c 是您可以在所有可能的解决方案中找到的最小 L1 范数。
使用 L1 范数的直觉是，由 L1范数等于常数c（|x1|+|x2|+|x3|+…+|xn| = c）形成的形状具有许多恰好稀疏的尖端（位于坐标系的一个轴上）。现在我们不断增加这个c（扩大形状的体积）来接触我们找到的解决方案（损失函数，通常是高维的曲面）。这两个形状在 L1 范数的尖端接触的概率非常高。这就是为什么你想把 L1 范数放入你的损失函数公式中，这样你就可以找到具有较小 c 的解决方案（在 L1 范数的“稀疏”尖端）。 （因此在真正的损失函数情况下，您实际上是在缩小红色形状以找到接触点，而不是从原点放大它。）
L1 范数是否总是在尖端触及解决方案并为我们找到稀疏解决方案？不一定。假设我们仍然想从 2D 点中找到一条线，但是这次，唯一的训练数据是一个点 [1, 1000]。在这种情况下，解线 b = 1000 -a 平行于 L1 范数形状的一条边：
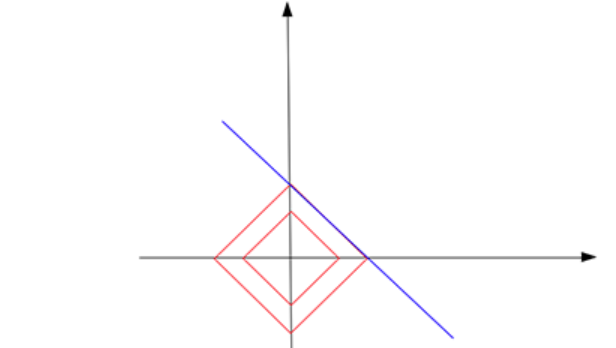
最终，它们接触到四边形的一条边，而不是尖端。 这次你不能找到一个唯一的解决方案，你的大部分正则化解决方案仍然不是稀疏的（除了两个尖端点）。
但是，触摸尖端的概率非常高。 我想这对于高维的现实世界问题更是如此。 当你的坐标系有更多的轴时，你的 L1 范数形状应该有更多的尖峰或尖端。 它必须看起来像仙人掌或刺猬!
如果你把一个人推向仙人掌，他被针刺伤的概率非常高。 这也是他们发明下面这种变态武器的原因，也是他们想要使用 L1 正则化的原因。
但是 L1 范数是找到稀疏解的最佳范数吗？ 好吧，事实证明，当 0 <= p < 1 时 Lp 范数给出了最好的结果。 这可以通过查看不同范数的形状来解释：
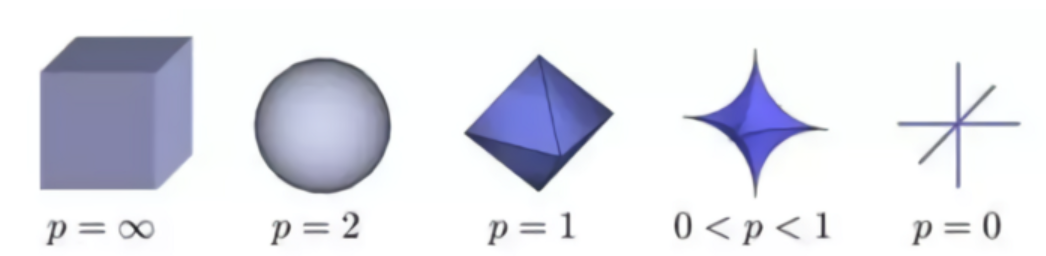
如你所见，当 p < 1 时，形状更“可怕”，具有更锐利、尖锐的尖峰。而当 p = 2 时，形状变成一个光滑的、没有威胁的球。那为什么不让 p < 1？那是因为当 p < 1 时，优化计算非常困难
正则化的真正作用是什么？
总之，当学习模型参数太多而训练数据又很少的时候很容易出现过拟合的问题。在这种情况下，模型往往会记住所有训练数据，包括噪声，以获得更好的训练分数。为了避免这种情况，将正则化应用于模型以减小其大小。正则化确保了模型是稀疏的，这样它的大部分分量都是零。这些零本质上是无用的，并且您的模型大小实际上已减小。
之所以使用 L1 范数求稀疏解，是因为它的特殊形状。它的尖峰恰好位于稀疏点。用它来接触解向量所在的曲面很可能会在尖端找到一个交点，从而得到一个稀疏的解。
想想这个：
