算法竞赛——进制换算你会了吗？

进制转换

网上查找了很多关于进制转换的博客，发现好多不同进制之间的转换代码实现过于复杂、冗余。而进制换算又是算法竞赛常常考到的基础知识点，清晰的代码实现是十分有必要的！今天我就针对常见的进制换算做一个详细、清晰的总结，希望对你的学习或者竞赛有些许帮助！

一、进制基本介绍

什么是进制？

就是进位制，是人们规定的一种进位方法。 对于任何一种进制–X进制，就表示某一位置上的数运算时是逢X进一位。
二进制就是逢二进一，八进制是逢八进一，十进制是逢十进一，十六进制是逢十六进一。

• 二进制表示的数中只能由0~1的数组成
• 八进制表示的数中只能由0~7的数组成
• 十六进制表示的数中只能由0~9 A~F的数（字符）组成

n进制如何数数？

十进制：0 1 2 3 4 5 6 7 8 9 10 11........

二进制：0 1 10 11 100 101 110 111 1000 1001 ......

八进制：0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21.......

十六进制：0 1 2 3 4 5 6 7 8 9 A B C D E F 10 .... 18 19 1A 1B 1C 1D.....

二、十进制与R进制之间的转换

十进制转R进制

十进制转成R进制的整数：除R取余法，结果倒过来取

注：十进制转16进制时，如果除出来的余数为10~15

10 ——> A

11 ——> B

12 ——> C

13 ——> D

14 ——> E

15 ——> F

R进制转10进制

R进制转成10进制的整数：按权展开

0~15转成二进制口算技巧：8421码

转为4位的二进制表示，4位的二进制数最多表示到15

8：2^3 4：2^2 2：2^1 1：2^0

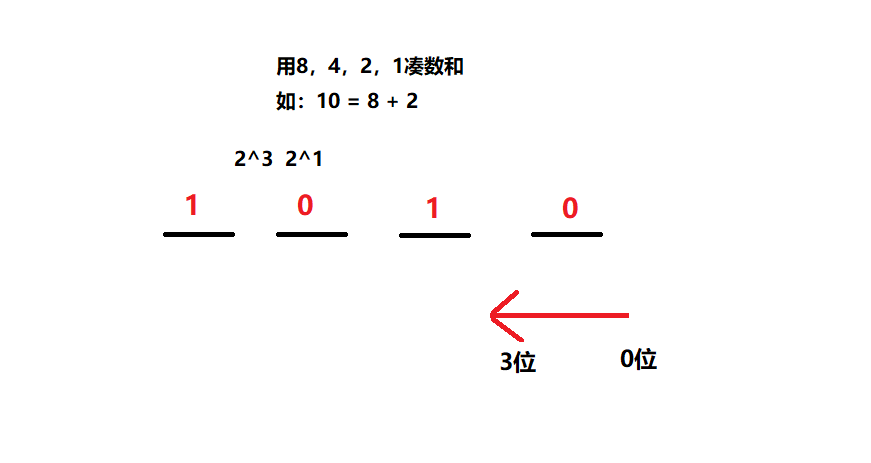
（一）十进制与二进制之间的转换

1.十进制转二进制

思路：用短除法除2求余，将结果逆序存储字符串string（你用数组逆序存也可以（栈），string其实说白了也是有数组的功能）

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, x;
char c;
string s; // 二进制结果

int main()
{   
    cin >> n;
    while(n != 0)
    {
        x = n % 2;// 获取结果
        c = x + '0';// 将数字转成字符
        s = c + s; // 将结果逆序存入字符串
        n /= 2; // 继续短除
    }
    
    // 这里不能用 n == 0判断特殊情况，因为while介绍 n 最后肯定为0 
    if(s == "") cout << 0;
    else cout << s;
    
    return 0;
}

2.二进制转十进制

题目描述

请将一个25位以内的2进制正整数转换为10进制！

输入

一个25位以内的二进制正整数

输出

该数对应的十进制

样例

输入

111111111111111111111111

输出

16777215

思路：

从最低位开始（size()-1），倒过来计算，按权展开。

字符转成整数：s[i] - '0'

准备变量t，表示2的n次方，t = 1，每次循环一次t = t * 2

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL t = 1, r; // t 表示权重; r 记录二转十的结果
string s; // 存放二进制

int main()
{   
    cin >> s;
    
    for(int i = s.size() - 1; i >= 0; i --)
    {
        r = r + (s[i] - '0') * t;
        t = t * 2;
    }
    cout << r;
    return 0;
}

（二）十进制与十六进制之间的转换

1. 十进制转十六进制

题目描述

请从键盘读入一个非负整数n（n是一个不超过18位的正整数），将n转换为16进制！

注意：16进制即逢16进1，每一位上可以是从小到大为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共16个大小不同的数，即逢16进1，其中用A，B，C，D，E，F这六个字母来分别表示10，11，12，13，14，15。

如：60的十六进制为3C。（字母请用大写）

输入

一个不超过18位的非负整数n

输出

该数的十六进制值

样例

输入

100000000000

输出

174876E800

思路：

短除法除16取余，结果逆序存储。逆序存储字符串时要注意：

当余数为：

​ 整数0~9，转换为字符'0'~'9'：x + '0'

​ 整数10~15，转换为字符'A'~'F'：x + 'A' - 10

注：

​ int 最多表达 2^31 - 1，10位整数；

​ long long 最多表达 2^63 - 1，19位整数

当数值超过int范围要开long long

【参考代码】

解法一：

分别判断 n%16的结果在0~9及10~15的那个范围，分别转换为对应的字符！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, x;
string s; // 存放二进制
char c;

int main()
{   
    cin >> n;
    while(n != 0)
    {
        x = n % 16;
        //将x转为字符逆序存入字符串s
        // 如果余数小于10：'0'~'9'
        // 如果余数10~15：'A'~'F'
        
        if(x < 10) c = x + '0';
        else c = x + 'A' - 10;
        
        s = c + s; // 逆序存入字符串
        
        n /= 16;
    }
    if(s == "") cout << 0;
    else cout << s;
    
    return 0;
}

解法二：

把0~15的字符结果罗列出来，根据余数直接取到相应的字符：string t = "0123456789ABCDEF"; // 技巧！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;

LL n, x;
string s; // 存放二进制
string t = "0123456789ABCDEF"; // 技巧！

int main()
{   
    cin >> n;
    while(n != 0)
    {
        x = n % 16;
        
        //将x转为字符逆序存入字符串s
        s = t[x] + s; // 逆序存入字符串
        
        n /= 16;
    }
    if(s == "") cout << 0;
    else cout << s;
    
    return 0;
}

2. 十六进制转十进制

题目描述

请将一个不超过10位的十六进制正整数转换为十进制整数！

输入

10位以内的十六进制正整数

输出

该数对应的十进制整数

样例

输入复制

2ECF

输出

11983

思路：逆序计算，按权展开！从s中获取每一位字符s[i]，要转换为实际的整数：

​ s[i]：'0'~'9' ——> s[i] - '0'

​ s[i]：'A~'F' ——> s[i] - 'A' + 10

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, r, t = 1;
string s; // 存放二进制



int main()
{   
    cin >> s;
    for(int i = s.size() - 1; i >= 0; i --)
    {
        // 如果s[i]是字符数字
        if(s[i] >= '0' && s[i] <= '9') // 用函数判断也可以 isdigit(s[i]):判断是不是字符数字
            r = r + (s[i] - '0') * t;
        else
            r = r + (s[i] - 'A' + 10) * t;
        
        t = t * 16;
        
    }
    cout << r;
    return 0;
}

三、二进制与八/十六进制的转换

我们知道二进制转为八/十六进制，可以先将二进制转为十进制，再用短除法求八/十六进制，但这样就比较麻烦，添加代码量！我们可以直接进行转换，就相当于一个模板！

原理：每位八进制数相当于3位二进制数（0_{7），每位十六进制数相当于`4位`二进制数（0}15）。在转换时，中间的0不能省略，开头不够时可以补零。

二进制转8/16进制：

8/16进制转二进制：

1.二进制转十六进制

题目描述

请将一个不超过100位的二进制数转换为十六进制数！

输入

一个不超过100位的二进制整数

输出

该数对应的十六进制数！

样例

输入

11001001111011111000001000010011

输出

C9EF8213

思路：

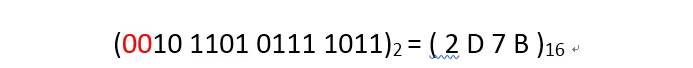
第一步：判断字符串的长度是否为4的倍数，如果不是则补0。

s：字符数组

s.size() % 4 == 1，补3个0

s.size() % 4 == 2，补2个0

s.size() % 4 == 3，补1个0

第二步：每四位2进制数转换成1位的16进制数（借助10进制在转）输出。

“1101”转换为对应的十进制整数 --> 13，注意判断转换的结果如果是0~9，转换为'0'~'9'，如果转换的结果是10~15，转换为'A'~'F'

将四位的二进制转换为1位的16进制：

char num(string s)
{
	...
}

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;

// 将4位的二进制转成10进制整数 在对应变为16进制符号：0~9 -> '0'~'9'; 10~15 -> 'A'~'F' 
char num(string s)
{
    LL r = 0, t = 1; // r = 0, t = 1;别忘了
    // 从最低位按权展开，转换为10进制
    // 10进制在转为16进制
    for(int i = s.size() - 1; i >= 0; i --)
    {
        r = r + (s[i] - '0') * t;
        t = t * 2;
    }
    
    //10进制转16进制： 0~9 -> '0'~'9'; 10~15 -> 'A'~'F'
    char c; // 存放结果
    if(r < 10) c = r + '0';
    else c = r + 'A' - 10;
    
    return c;
}


int main()
{   
    string s, t; // 存放二进制
    cin >> s; 
    
    // 看是否需要补零
    if(s.size() % 2 == 1) s = "000" + s;
    else if(s.size() % 2 == 2) s = "00" + s;
    else if(s.size() % 2 == 3) s = "0" + s;
    
    // 每每截取4位二进制数：substr(i, 4)截取字符串，i += 4
    for(int i = 0; i < s.size(); i += 4)
    {
        t = s.substr(i, 4);
        // 将4位二进制转换为16进制，输出
        cout << num(t);
    }

    return 0;
}

2.十六进制转二进制

思路：将每一位的16进制数，转换位4位的二进制数！

第一步：将每位的16进制转换为4位的2进制，连接到字符串上！

第二步：清除前导0，也就是要从第一个非0开始输出。注：当16进制为0000时，转成二进制后也为0，此时不能把0000全部清除掉，要保留一个0！

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
// 技巧：
string t[16] = {"0000","0001","0010","0011","0100","0101","0110","0111","1000","1001","1010","1011","1100","1101","1110","1111"};


//求： 将每位16进制转为对应的4为二进制
//1. 将s[i]转换为0~15对应的整数，再求对应的4位2进制（技巧：通过数组下标获取对应二进制）
//2. 最终清除二进制字符串的前导0
int main()
{   
    string s, r; // s存放16进制; r存放2进制
    cin >> s; 
    
    for(int i = 0; i < s.size(); i ++)
    {
        //1. 将s[i]转换为0~15对应的整数
        int x;
        if(s[i] >= '0' && s[i] <= '9') x = s[i] - '0'; // 如果是0~9
        else x = s[i] - 'A' + 10;
        
        //1. 用字符串拼接16进制所对应表示的2进制
        r += t[x];
    }
    
    //2. 最后清除前导0
    while(r[0] == '0' && r.size() > 1)
    {
        r.erase(0,1);
    }
    
    cout << r;

    return 0;
}

C++ STL中的：erase()函数的功能是用来删除容器中的元素

erase(first，last)；------>左闭右开： [first，last)

3.二进制转八进制

题目描述

请将一个100位以内的二进制整数转换为8进制整数！

输入

100位以内的二进制整数

输出

该数对应的八进制整数

样例

输入

111100001111000011110000

输出

74170360

思路：同上述二进制转16进制

第一步：判断字符串的长度是否为3的倍数，如果不是则补0。

s：字符数组

s.size() % 3 == 1，补2个0

s.size() % 4 == 2，补1个0

第二步：每三位2进制数转换成1位的8进制数（0_{7）输出。（每3位的二进制数是：0}8，9的话是1001四位了！），即转成对应10进制即可

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;

// 将3位的二进制(一定是0~7) 转成 10进制整数 对应的8进制必定也是：0 ~ 7
LL num(string s)
{

    LL t = 1, r = 0;
    // 从最低位按权展开，转换为10进制
    for(int i = s.size() - 1; i >= 0; i --)
    {
        r = r + (s[i] - '0') * t;
        t = t * 2;
    }
    
    return r;
}

int main()
{   
    string s, t; // s存放二进制
    cin >> s;
    
    // 看是否需要补0
    if(s.size() % 3 == 1) s = "00" + s;
    else if(s.size() % 3 == 2) s = "0" + s;
    
    // 截取3位二进制，转为对应的八进制，输出
    for(int i = 0; i < s.size(); i += 3)
    {
        t = s.substr(i, 3);
        
        // 将每每3位二进制转为八进制并输出
        cout << num(t);
    }

    return 0;
}

4.八进制转二进制

题目描述

请将一个100位以内的8进制整数转换为2进制整数！

输入

100位以内的8进制整数

输出

该数对应的2进制整数

样例

输入

12376532347173217361

输出

1010011111110101011010011100111001111011010001111011110001

思路：同16进制转二进制：将每一位的8进制数，转换为3位的二进制数！

第一步：将每位的8进制（0~7）转换为3位的2进制，连接到字符串上！

第二步：清除前导0，也就是要从第一个非0开始输出。注：当8进制为000时，转成二进制后也为0，此时不能把000全部清除掉，要保留一个0！

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;

// 存储0~7 八进制对应的 3位二进制
string t[8] = {"000","001","010","011","100","101","110","111"};


int main()
{   
    string s, r; // s存放八进制，r存放二进制
    
    cin >> s;
    
    // 8进制 ——> 2 进制：将每一位8进制转换为3位的2进制（通过数字对应数组直接获取！）然后拼接
    for(int i = 0; i < s.size(); i ++)
    {
        int x = s[i] - '0'; // 找到每一位8进制所对应的2进制表示
        r += t[x]; // 拼接
    }
    
    // 清除前导0
    while(r[0] == '0' && r.size() > 1)
    {
        r.erase(0, 1);
    }
    
    cout << r;
    
    return 0;
}

进制转换应用例题：小丽找半个回文数

求这个数在十进制下不是回文数，但在2进制或者16进制下是回文数，则这个数是半个回文数！

思路：

朴素的想法，判断这个十进制数是否是回文数，如果不是则将其转为2进制数和16进制数，再判断是否是回文数！

我们发现一个很相似的操作，那就是这个数在d进制表示下，是否是回文数，我们知道10进制数转为其它进制使用的是短除法！，我们不必用进制表示的最终结果来判断是否是回文，我们可以将每一位余数存到一个数组中，判断它的余数是否为回文即可！——因此，我们可以写个判断函数进行判断统一判断就可以啦！

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>


using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, x;
int a[N]; // 存储n转为d进制的每一位对应的余数，用来判断是否是回文数

// 将 十进制数 n 转换为 d进制数 并判断它是不是回文！
bool huiwen(int n, int d)
{ 
    int k = 0;
    while(n != 0)
    {
        x = n % d;
        a[k ++] = x; // 存储余数
        n /= d;
    }
    // 判断回文：对称位是否相等，出现不等则不是回文数
    for(int i = 0; i < k / 2; i ++)
    {
        //0 --> k - 1
        //1 --> k - 2
        //2 --> k - 3... i --> k - i - 1
        if(a[i] != a[k - i -1])
        {
            return false;
            break;
        }
    }
    
    return true;
}

int main()
{   
    cin >> n;
    while(n --)
    {
        int x;
        cin >> x;
        if(huiwen(x, 10) == false && (huiwen(x, 2) == true || huiwen(x, 16) == true))
        {
            cout << x << endl;
        }
    }
    
    return 0;
}

四、总结

进制转换可以通过类比10进制计算机制来换算，清楚转换的原理公式即可。再8/16进制转2进制时，使用一个字符串数组记录对应的8/16每一位的3/4位二进制表示，转换时直接使用，加快效率！

注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦