入门级别递推算法
递推算法
什么是递推
递推就是一种若干步可重复运算来描述复杂问题的方法,递推是一种重要的数学方法,也是编程编程解决问题的常用方法。————小到大,已知推出未知
递推有什么特征
特点:一个问题求解需要一系列计算,这一系列的计算的步骤中存在着关联关系;在计算时,如果可以找到前后过程之间的数量关系(即递推式),那么就可以从已知条件推导出最终结果!
如等差数列就可以用递推公式求出:
1 3 5 7 9
由小到大,通过已知及其数量关系找出递推式推出未知:
A(n) = A(n - 1) + 2
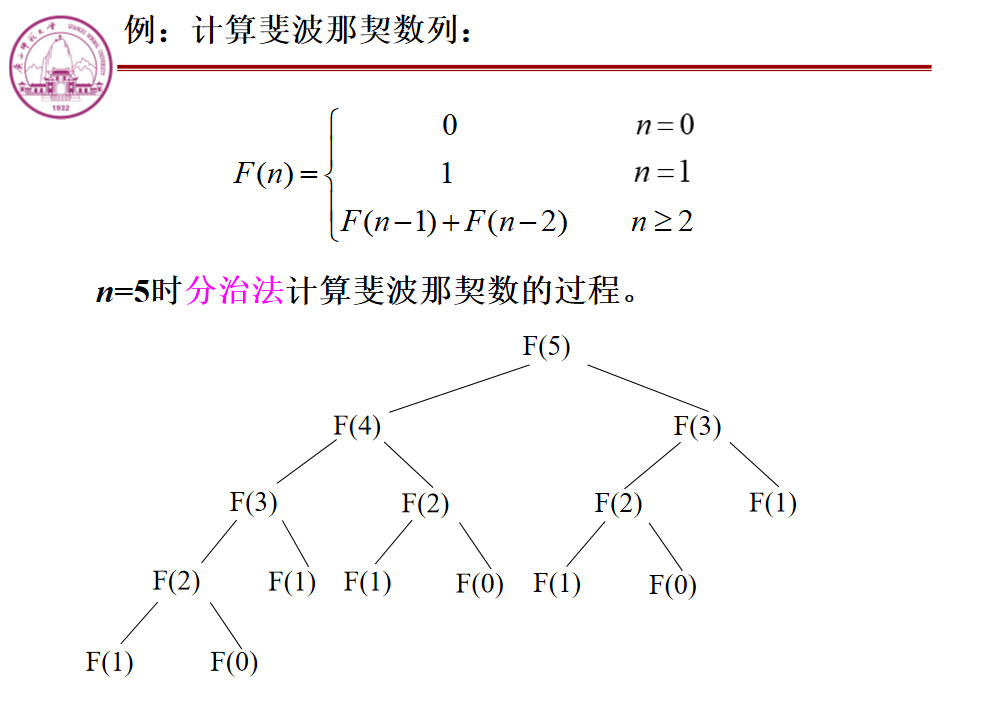
求斐波那契数列的第 n 项
请使用递归的方式求斐波那契数列的第 n 项。
斐波那契数列:1,1,2,3,5…,这个数列从第 3 项开始,每一项都等于前两项之和
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示斐波那契数列的第 nn 项。
数据范围
1≤n≤30
输入样例:
4输出样例:
3
递归做法:
当n越来越大时,执行时间会越来越长,直到超时(时间复杂度:指数级别)
因为随着n的增大,重复解的项就会越来越多(但又不得不计算),这棵树就会越来越大,耗时也增大!
【参考代码】
#include<iostream>
using namespace std;
int f(int n)
{
if(n == 0 || n == 1) return 1;
return f(n - 1) + f(n - 2);
}
int main()
{
int n;
cin>>n;
cout<<f(n);
return 0;
}
改进方法:使用数组和递推的方法提高递归的效率
上述时间超限,那我们可以通过减少不必要的计算来降低复杂度,即减少重复的计算,那我们可以通过递推的方式来优化——可以用一个数组来记录重复计算的结果,当下次再用时,直接使用即可!

【参考代码】
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL a[N], n;
int f(LL n)
{
// 已知量
a[1] = 1;
a[2] = 2;
// 小到大,已知到未知,有关系得出递推公式
for(int i = 3; i <= n; i ++)
{
a[i] = a[i - 1] + a[i - 2];
}
return a[n];
}
int main()
{
cin>>n;
cout<<f(n);
return 0;
}
改进方法:利用变量迭代的方法提高递归的效率
采用两个变量x和y分别记录 n - 1项的数和n- 2项的数
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL x, y, n, z;
int main()
{
cin >> n;
x = 1;
y = 1;
// 1 1 2 3 5 1 1 2 3 5
// x y z x y z
for(int i = 3; i <= n; i ++) // z 为前两项的和故可以使用迭代 —— 减少重复的计算
{
z = x + y;
x = y;
y = z;
}
if(n < 3) cout << 1 ;
else cout << z;
}
猴子吃桃问题
思路:第二天吃掉剩下的一半多一个,第十天还剩下1个。有已知到未知,可以从后往前递推!
10 :1
9:4 (2 * (1 + 1))
8:10 (2 *(4 + 1))
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL x, y, n, z;
int main()
{
int ans = 1;
for(int i = 9; i >= 1; i --)
{
ans = 2 * (ans + 1);
}
cout << ans;
}
Pell数列
题目描述
有一种数列,它的前10项的值分别为:1 2 5 12 29 70 169 408 985 2378,这个数列被称为Pell数列,请问该数列的第n项的值是多少?(n<=1000)
输入
一个整数n
输出
第n项的值
样例
102378
思路:
不难看出从第3项开始,每一项的数等于前一项数的两倍与前前一项的和。
但是当n和大时,结果就很大很大超出了int 甚至long long的范围而导致数据溢出,因此还要用到高精度算法!
求和时可以用迭代求和!
1 2 5 12 ....
递推公式:An = 2*A(n - 1 ) + A(n - 2)
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
LL n;
string add(string a, string b)
{
// 记录答案
string res;
vector<int>A, B, C;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); //A = [6,5,4,3,2,1];
for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
// 大的在上,小的在下
if(A.size() < B.size()) return add(b,a);
int t = 0; // 进位
for(int i = 0; i < A.size(); i ++)
{
t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);// 记录答案
t /= 10; // 进位
}
// 判断最后一位是否需要进位!
if(t) C.push_back(1);
for(int i = C.size() - 1; i >= 0; i --) res += (C[i] + '0');
return res;
}
string mul(string a)
{
string res;
vector<int>A, C;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
int t = 0; //用t来记录乘积结果以及进位
for(int i = 0; i < A.size(); i ++)
{
t += A[i] *2;
C.push_back(t % 10);
t /= 10;
}
// 判断最后一位是否要进位
while(t)
{
C.push_back(t % 10);
t /= 10;
}
// 去除前导0
while(C.size() > 1 && C.back() == 0) C.pop_back();
for(int i = C.size() - 1; i >= 0; i --) res += (C[i] + '0');
return res;
}
int main()
{
// An = 2*A(n - 1 ) + A(n - 2)
string x, y, z;
cin >> n;
x = "1";
y = "2";
if(n == 1) cout << x;
else if(n == 2) cout << y;
else // 从第三项开始递推(迭代求和)
{
for(int i = 3; i <= n; i ++)
{
//1 2 5 12 1 2 5 12
//x y z x y z
z = add(mul(y), x);
// 修改x,y的值,逐步往后推导
x = y;
y = z;
}
cout << z;
}
return 0;
}
数木块
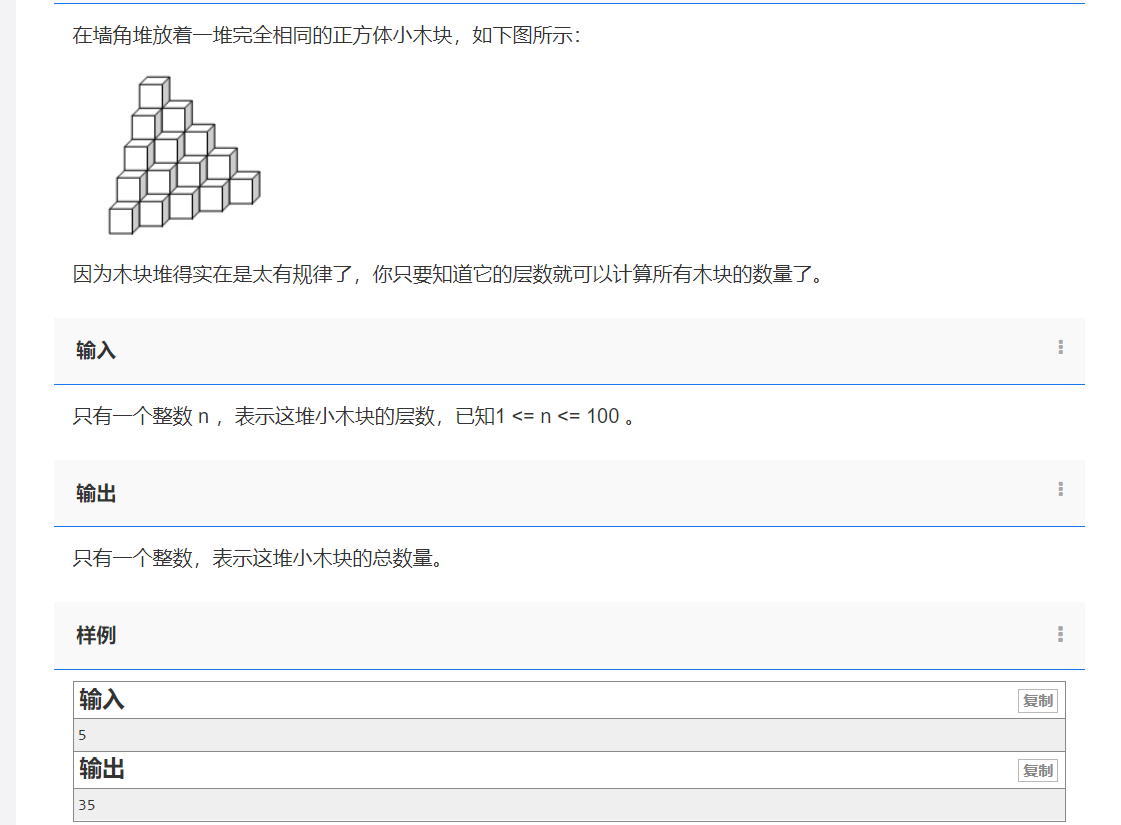
思路:
第1层:1个
第2层:3个
第3层:6个
第4层:10个
.....
第i层的木块 = i + 上一层的木块数量
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL x, y, n, z;
int a[110];
int main()
{
cin >> n;
a[1] = 1;
int sum = 0;
for(int i = 2; i <= n; i ++) // 从第2层开始
{
a[i] = i + a[i - 1];
sum += a[i];
}
if(n == 1) cout << 1;
// 加上第一层的木块
else cout << sum + 1;
}
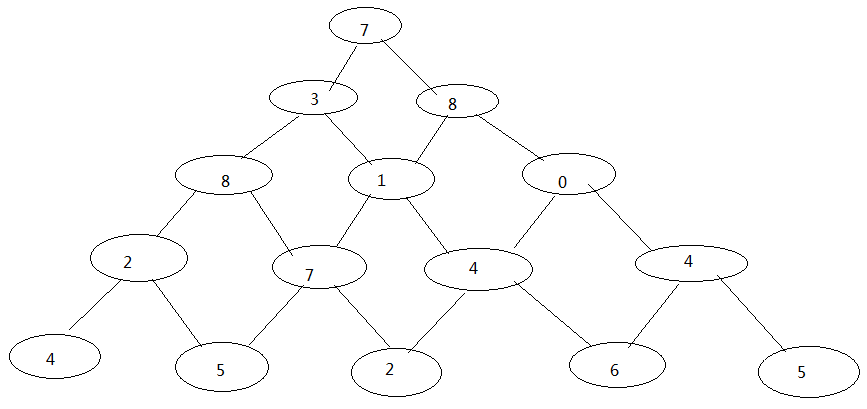
数塔问题
题目描述
有如下所示的数塔,要求从底层走到顶层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
输入
输入数据首先包括一个整数整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
输出
从底层走到顶层经过的数字的最大和是多少?
样例
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 530
思路:
从底层走到顶层经过的数字的最大和是多少?
我们可开一个二维数组来记录走到某一个位置时数字的最大和是多少,由于数都是已知的,由已知到未知,由小到大,我们可以从底部递推到顶部,最后一行的最大值就是自己本身,从n-1行开始,改行上每一个位置的最大和由正下方和左下方的数来决定,要使得和最大,那么就从正下方和左下方的数中选择较大的那一个!层层往上递推,最终顶部位置的和就最大。
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL x, y, n, z;
int a[110][110];
int main()
{
cin >> n;
// 读入数塔
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= i; j ++){
cin >> a[i][j];
}
}
// 从第 n- 1行开始 往上递推!
for(int i = n - 1; i >= 1; i --){
for(int j = 1; j <= n - 1; j ++){
a[i][j] = a[i][j] + max(a[i + 1][j], a[i + 1][j + 1]);
}
}
cout << a[1][1];
}
过河卒
题目描述
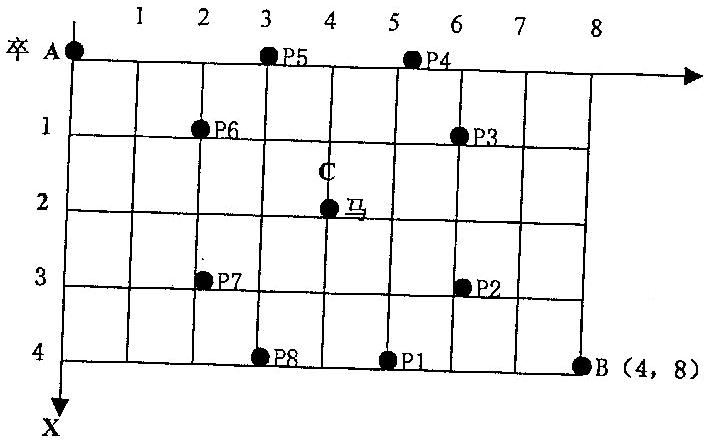
A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如下图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如下图 C 点可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。 棋盘用坐标表示,现给定A 点位置为(0,0)B 点位置为(n,m)(n,m 为不超过 20 的整数),马的位置为C(X,Y)(约定: C点与A点不重叠,与B点也不重叠)。要求你计算出卒从 A 点能够到达 B 点的路径的条数。
输入
B点的坐标(n,m)以及对方马的坐标(X,Y)(马的坐标一定在棋盘范围内,但要注意,可能落在边界的轴上)
输出
样例
输入
6 6 3 2输出
17
思路:
注:卒行走规则:可以向下、或者向右
当没有马时由起点到终点由几种方案呢?
那如果存在障碍物呢?也就是马儿以及马儿所控制的范围!
- 我们可以将棋盘初始化设计为1
- 标记马和马所控制的点为0
- a[0] [0]不用计算,除此以为
- i = 0,第一行,除了控制点,a[i] [j]等左侧的值
- j = 0,第一行,除了控制点,a[i] [j]等正上方的值
- 其余的点,除了控制点和原点以外,a[i] [j] = 左侧 + 正上方
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n, m, x, y;
int a[110][110];
int main()
{
//读入终点坐标 和 马的坐标
cin >> n >> m >> x >> y;
// 初始化棋盘
for(int i = 0; i <= n; i ++){
for(int j = 0; j <= m; j ++){
a[i][j] = 1;
}
}
// 标记马的控制点,马及其八个方向!
a[x][y] = 0;
if(x - 2 >= 0 && y + 1 <= m) a[x - 2][y + 1] = 0;
if(x - 1 >= 0 && y + 2 <= m) a[x - 1][y + 2] = 0;
if(x + 1 <= n && y + 2 <= m) a[x + 1][y + 2] = 0;
if(x + 2 <= n && y + 1 <= m) a[x + 2][y + 1] = 0;
if(x + 2 <= n && y - 1 >= 0) a[x + 2][y - 1] = 0;
if(x + 1 <= n && y - 2 >= 0) a[x + 1][y - 2] = 0;
if(x - 1 >= 0 && y - 2 >= 0) a[x - 1][y - 2] = 0;
if(x - 2 >= 0 && y - 1 >= 0) a[x - 2][y - 1] = 0;
// 递推计算
for(int i = 0; i <= n; i ++){
for(int j = 0; j <= m; j ++){
if(i == 0 && j == 0) continue; // a[0][0] 不用算
if(a[i][j] == 0) continue;// 马控制的点不需要算
if(i == 0) a[i][j] = a[i][j - 1];// 第一行
else if(j == 0) a[i][j] = a[i - 1][j];// 第一列
else
{
a[i][j] = a[i][j - 1] + a[i - 1][j];
}
}
}
cout << a[n][m];
}
数花生问题
(动态规划)
题目描述
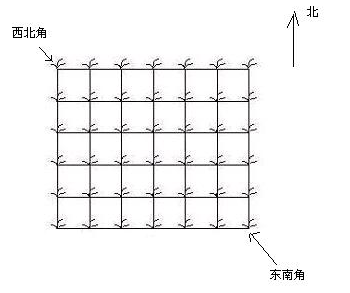
Hello Kitty 想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty只能向东或向南走,不能向西或向北走。问Hello Kitty 最多能够摘到多少颗花生。
如输入:
2 2
1 1
3 4
代表有2行,每行有2株花生,那么摘能摘到的最多的花生就是:1->3->4,总和为8颗花生。输入
第一行是两个整数m和n(m<=100,n<=100),代表了花生地里有m行,每行有n列的花生!
后面m行,每行有n个整数代表了每行中,每株花生的数量!
输出
输出是一个整数,代表了最多能摘到的花生的总数
样例
输入
2 2 1 1 3 4输出
8
【参考代码】
a[i] [j]:表示走到(i,j)位置所获得的最多花生!
递推公式: a[i][j] = a[i][j] + max(a[i][j - 1], a[i - 1][j])
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110;
LL m, n;
int a[N][N];
int main()
{
cin >> m >> n;
memset(a, 0, sizeof a); // 初始化数组为0
// 读入地图
for(int i = 1; i <= m; i ++){
for(int j = 1; j <= n; j ++){
cin >> a[i][j];
}
}
// a[i][j]:表示走到(i,j)位置所获得的最多花生
for(int i = 1; i <= m; i ++){
for(int j = 1; j <= n; j ++){
a[i][j] = a[i][j] + max(a[i][j - 1], a[i - 1][j]);
}
}
cout << a[m][n];
return 0;
}
蜜蜂路线
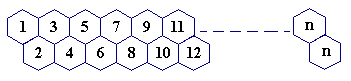
题目描述
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房M开始爬到蜂房N,1=<M<N<=100,有多少种爬行路线?
输入
输入M,N的值。 (1=<m<n<=100)
输出
爬行有多少种路线。
样例
输入
1 14输出
377
思路:
它只能从标号小的蜂房爬到标号大的相邻蜂房
我们想从1 ——> n 分析有多少步数
f(n)表示走1到n的所有步数
f(1) = 1
f(2) = 1
f(3) = 2
f(4) = 3 ........
我们发现从第3项开始,每一项的结果都为前两项的和!,每项的结果都必定有前两项决定!—— 也就是斐波那契数列
那么从 N —— M呢?
例如:7 —— > 10有几种 —— 要走到10,必然要先到8或9
7 —— > 7:1 (自己到自己也是1种)
7 ——> 8:1
7 ——> 9:2
7 ——> 10:3
我们发现更换了起始点丝毫不影响,还是个斐波那契数列,值得注意的是当n很大时,就会溢出,因此要用高精度算法!
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110;
LL m, n;
int a[N];
int main()
{
cin >> m >> n;
a[m] = 1, a[m + 1] = 1;
for(int i = m + 2; i <= n; i ++)
{
a[i] = a[i - 1] + a[i - 2];
}
cout << a[n];
return 0;
}
当数据很庞大时,求和的结果就会溢出————高精度算法来解决这一求和过程
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110;
LL m, n;
int a[N];
string add(string a, string b)
{
if(a.size() < b.size()) return add(b, a); //保证大的在上
string res;
vector<int> A, B, C;
for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
int t = 0;
for(int i = 0; i < A.size(); i ++)
{
t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(1);
for(int i = C.size() - 1; i >= 0; i --) res += (C[i] + '0');
return res;
}
int main()
{
cin >> m >> n;
string x = "1";
string y = "1";
string z;
for(int i = m + 2; i <= n; i ++) // 迭代求和
{
// 1 1 2 3 5 1 1 2 3 5
// x y z x y z
z = add(x, y);
x = y;
y = z;
}
cout << z;
return 0;
}
骨牌问题
题目描述
有1×n(n<=50)的一个长方形,用一个1×1、1×2和1×3的骨牌铺满方格,请问有多少种铺法?
例如当n=3时为1×3的方格。此时用1×1、1×2和1×3的骨牌铺满方格,共有四种铺法。如下图:
输入
一个整数n(n<=50)
输出
骨牌的铺法
样例
34
n为4的时候,方法数F4的分析如下:
第一块放11,有一种方法;剩余3块方法数是F3=4种。根据乘法原理,该种情况的方法数是14=4。
第一块放12,有一种方法;剩余2块方法数是F2=2种。根据乘法原理,该种情况的方法数是12=2.
第一块放13,有一种方法;剩余1块方法数是F1=1种。该种情况方法数是11=1.
根据分类原理,F4=4+2+1=7种。
……
故n>=4的时候,Fn=Fn-1+Fn-2+Fn-3
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110;
LL m, n;
int a[N];
int main()
{
cin >> n;
a[1] = 1;
a[2] = 2;
a[3] = 4;
// 从第4项开始每一项都是前一项的2倍数
for(int i = 4; i <= n; i ++)
{
a[i] = a[i - 1] + a[i - 2] + a[i -3];
}
cout << a[n];
return 0;
}
小X放骨牌
小X喜欢下棋。
这天,小X对着一个长为N宽为M 的矩形棋盘发呆,突然想到棋盘上不仅可以放棋子, 还可以放多米诺骨牌。
每个骨牌都是一个长为2宽为1的矩形,当然可以任意旋转。小X想知道在骨牌两两不重叠的前提下,这个棋盘上最多能放多少个骨牌,希望你帮帮他。输入
第一行包含用一个空格隔开的两个整数N,M。
输出
第一行包含一个整数,表示该棋盘上最多能放的骨牌个数。
样例
输入
2 3输出
3提示
如图所示,三种颜色分别对应了三个骨牌。
数据范围
对于30%的数据,N,M≤4。
对于60%的数据,N,M≤1000。
对于 100%的数据,1≤N,M≤40000。
放的牌子都是2个!
可以从小的行列来推出关系
不论是偶数*偶数还是偶数*奇数还是奇数*奇数都是(n * m)/2,最多填的只能是2的倍数!
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110;
LL m, n;
int a[N];
int main()
{
cin >> n >> m;
cout << (n * m) / 2;
return 0;
}
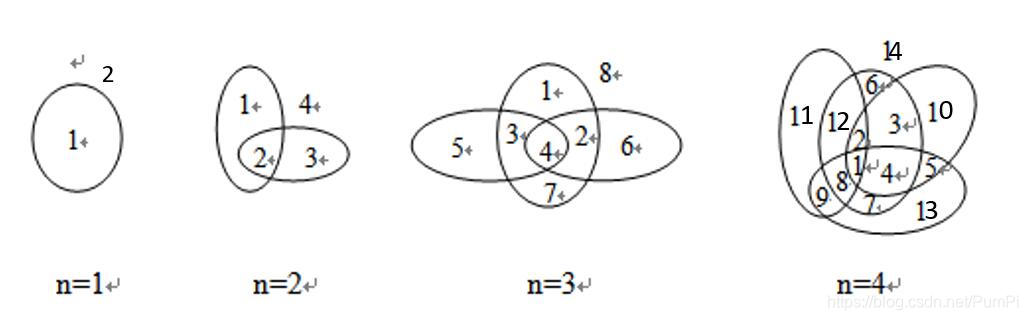
平面分割问题
设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
输入
一个整数n(n<=10000),代表封闭曲线的条数
输出
n条曲线分割区域的个数
样例
24
当前平面的个数等于前一个图形平面的个数加上新增的平面的个数。
前一个平面的个数就是a[n-1]。新增的平面的个数恰好是上一图椭圆数量的两倍,也就是2*(n-1)。
所以递推式就是:a[i]=a[i-1] + 2*(i-1);
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL m, n;
LL a[N];
int main()
{
cin >> n;
a[1] = 2;
for(int i = 2; i <= n; i ++)
{
a[i] = a[i - 1] + 2 * (i - 1);
}
cout << a[n];
return 0;
}