数组手撕堆，你学会了吗？
堆
一、堆的基本介绍
1.堆的概念：
如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<=K2i+2 ，则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆，否则叫做大根堆。STL 中的 priority_queue 其实就是一个大根堆。
2.堆的性质：
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。
完全二叉树：除最后一层节点以外，其它层的节点都是满的，且最后一层从左到右依次排布的二叉树就称为完全二叉树。
3.堆的两种结构：
小根堆：堆顶元素最小
大根堆：堆顶元素最大
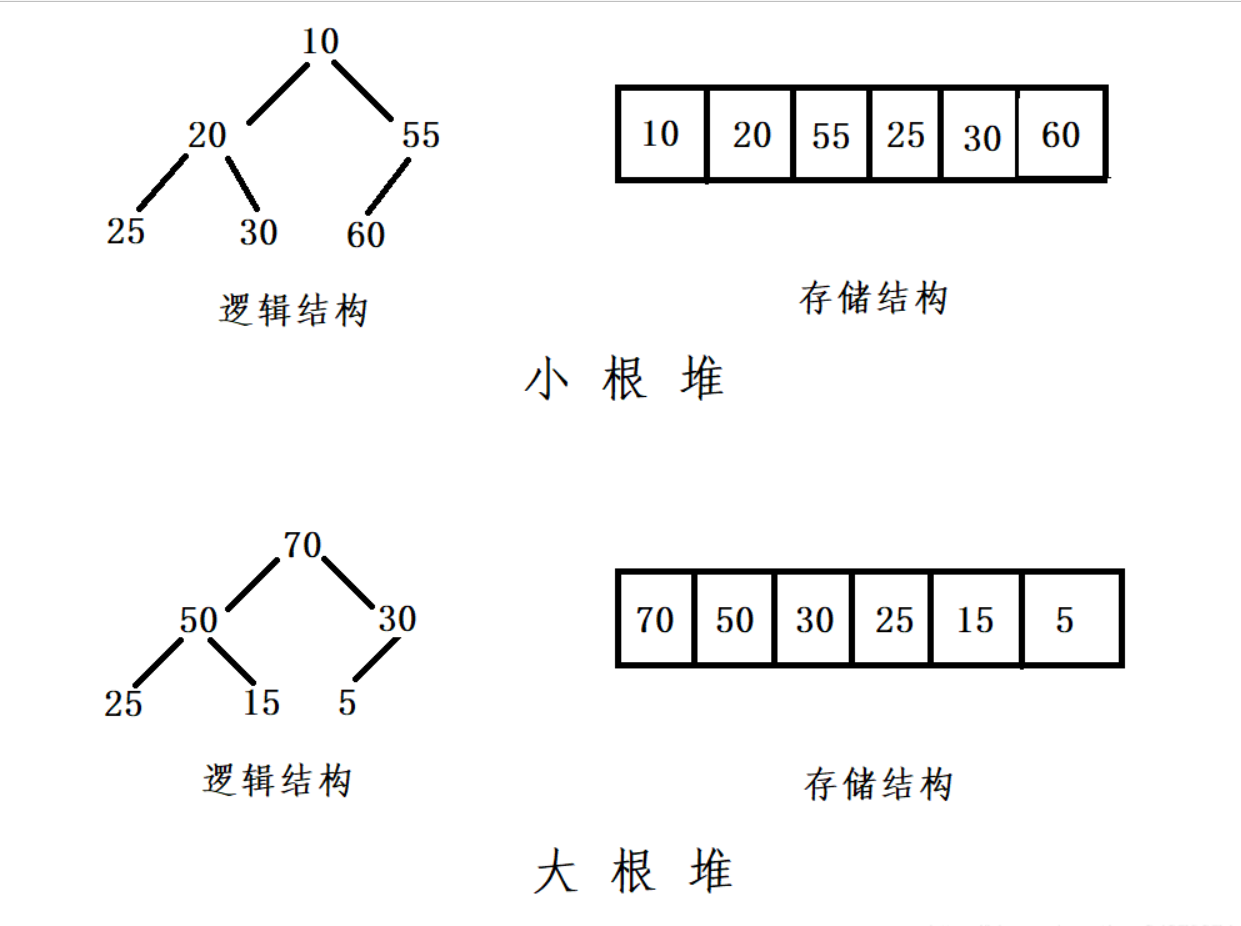
3.堆/完全二叉树的存储：
用一个一维数组来维护
x的左孩子（位置）：2i
x的右孩子（位置）：2i + 1
注：下标从1开始，方便维护
二、堆的五个操作
1.插入一个数
插入一个数：在堆的最后一个位置添加x；不断往上移（调整堆，使其满足小根堆性质）
heap[++ sizes] = x;
up(size)
2.求堆的最小值
求堆的最小值：小根堆的第一个元素就是最小值
heap[1];
3.删除最小值
删除操作指删除堆中最小的元素，即删除根结点。
但是如果直接删除，则变成了两个堆，难以处理。
所以不妨考虑插入操作的逆过程，设法将根结点移到最后一个结点，然后直接删掉。
然而实际上不好做，我们通常采用的方法是，把根结点和最后一个结点直接交换。
于是直接删掉（在最后一个结点处的）根结点（size --），但是新的根结点可能不满足堆性质……
向下调整：在该结点的儿子中，找一个最小的，与该结点交换，重复此过程直到底层。
可以证明，删除并向下调整后，没有其他结点不满足堆性质。
时间复杂度 O(logn)。
// 用最后一个点覆盖第一个点;size --;down(1)
heap[1] = heap[size]; // 用最后一个点覆盖第一个点 （**数组模拟我们直接覆盖就行**）
size --; // 将最后一个点从数组中删去
down(1); // 让1号点往下走（调整堆使满足小根堆性质）
4.删除任意一个元素
删除任意一个元素与删除最小值（根节点很相像）
删除第k的元素，我们将最后一个元素将他覆盖后，无非就这三种情况：不变，比他大，比他小，因此就是不同的维护方式（但只会选择一种方式去维护），不管37 21 down(k), up(k);都执行就可以了，down(k), up(k)只会执行一个。
// 删除第k个元素
heap[k] = heap[size];
size --;
down(k), up(k); //只会执行一个
5.修改任意元素
当我们将第k个元素修改之后，就要维护堆（同上述操作4）
heap[k] = x;
down(k), up(k); //只会执行一个
三、堆的调整/维护：
上述的五个操作都可以通过down(i)和up(i)操作调整维护堆来实现！
调整是对是位置（下标）进行调整，下标对应着数组中的值！
1.向下调整：down(i)
down(i)：当某个节点的值大了，就将它往下调整
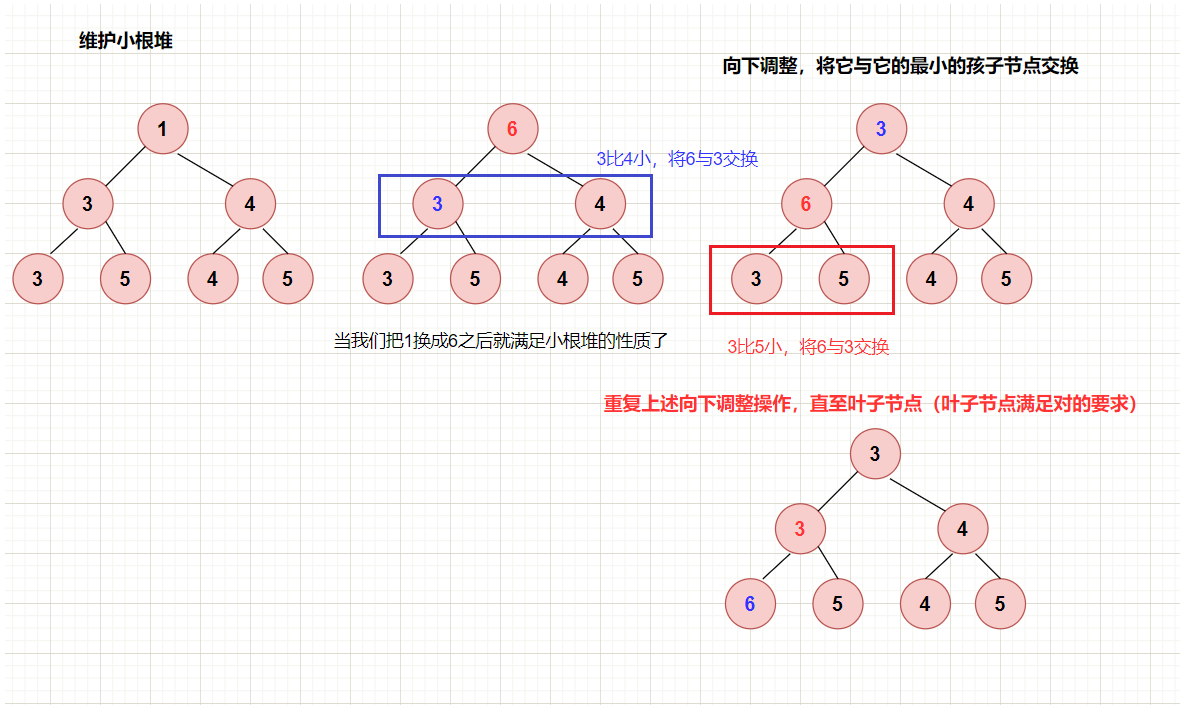
down()操作其实是一个递归的过程，从根节点开始，如果当前这个点比某一个子节点要大的话，就将它们交换，换完之后递归处理即可！
void down(int i)
{
int t = i;
if(2 * i <= sizes && heap[2 * i] < heap[t]) t = 2 * i; // 如果左孩子存在，且小于根节点
if(2 * i + 1 <= sizes && heap[2 * i + 1] < heap[t]) t = 2 * i + 1;// 如果右孩子存在，且小于根节点
if(t != i) // heap[t] 是最小值
{
swap(heap[i], heap[t]);
down(t); // 交换之后继续维护调整堆
}
}
1.1.初建堆
我们如何将一个无序序列（数组）调整成堆（小根堆）呢？
// 将数组建成堆：从n/2 down()到1（调整到1）
for (int i = n/2; i >= 1 ; i --) down(i);
1.2.堆排序
康康这个例题：
输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。
输入格式
第一行包含整数 n 和 m。
第二行包含 n 个整数，表示整数数列。
输出格式
共一行，包含 m 个整数，表示整数数列中前 m 小的数。
数据范围
51≤m≤n≤105，
1≤数列中元素≤109输入样例：
5 3
4 5 1 3 2输出样例：
1 2 3
思路：
构造一个小根堆，每次将堆顶元素输出，然后删去堆顶元素，维护小根堆down()操作（得到第二小的堆顶元素）.....
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int heap[N], sizes;
// down()操作其实是一个**递归**的过程，从该根节点开始，
// 如果当前这个点比某一个子节点要大的话，就将它们交换，换完之后递归处理即可！
void down(int i)
{
int t = i;
if(2 * i <= sizes && heap[2 * i] < heap[t]) t = 2 * i; // 如果左孩子存在，且小于根节点
if(2 * i + 1 <= sizes && heap[2 * i + 1] < heap[t]) t = 2 * i + 1;// 如果右孩子存在，且小于根节点
if(t != i) // heap[t] 是最小值
{
swap(heap[i], heap[t]);
down(t); // 交换之后继续维护调整堆
}
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &heap[i]);
sizes = n;
// 将数组建成堆：从n/2 down()到1（调整到1）
for (int i = n/2; i >= 1 ; i --) down(i);
while (m -- )
{
printf("%d ", heap[1]); // 每次输出堆顶元素（最小值）
// 输出堆顶元素（最小值）后，将其删去，维护堆，拿到下一个min
heap[1] = heap[sizes];
sizes --;
down(1);
}
return 0;
}
2.向上调整：up(i)
up(x)：当某个节点的值小了，就将它往上调整
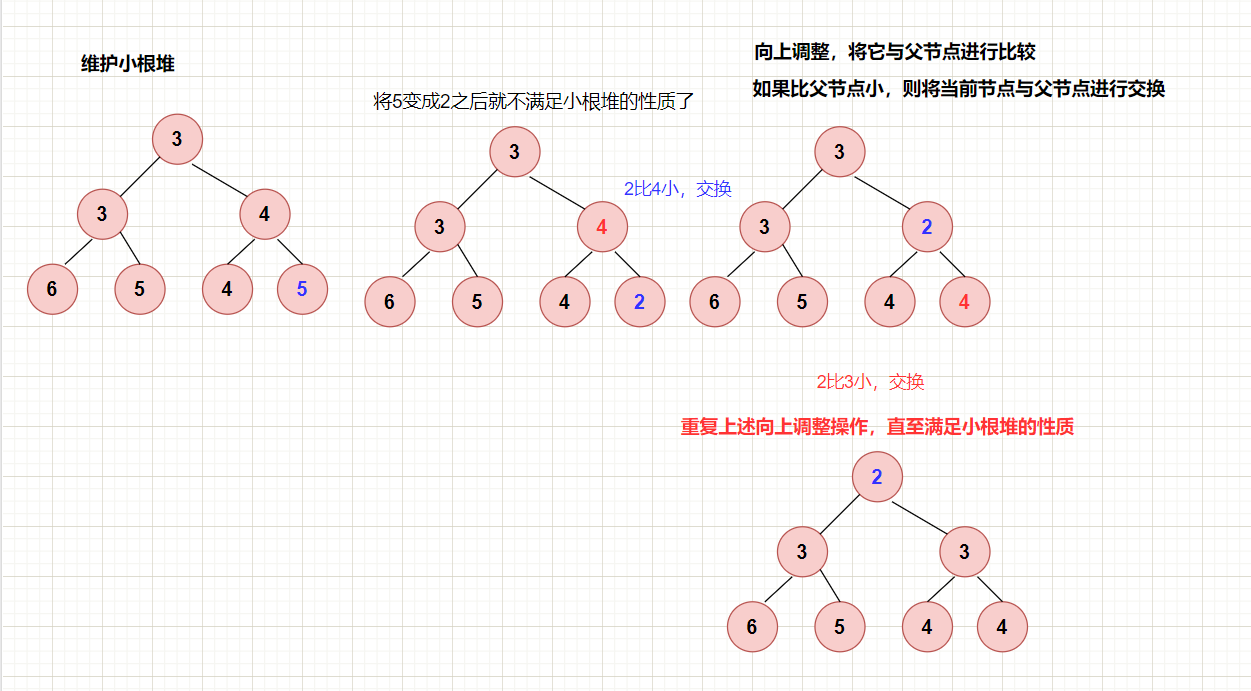
具体代码：（递归小根堆）
void up(int u)
{
int t=u; //up中的t保存的是父结点
if(u/2 && h[u/2]>h[t]) t=u/2; //up操作中只需要判断up儿子与根的大小就可
if(t!=u) //递归操作
{
h_swap(t,u);
up(t);
}
}
具体代码：（y总循环）
void up(int u)
{
while(u/2 && h[u/2]>h[u])
{
h_swap(u/2,u);
u/=2;
}
}
四、堆完整模板
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;
// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);
数组模拟堆
维护一个集合，初始时集合为空，支持如下几种操作：
I x，插入一个数 xx；PM，输出当前集合中的最小值；DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；D k，删除第 kk 个插入的数；C k x，修改第 k 个插入的数，将其变为 x；现在要进行 N 次操作，对于所有第 2 个操作，输出当前集合的最小值。
输入格式
第一行包含整数 NN。
接下来 NN 行，每行包含一个操作指令，操作指令为
I x，PM，DM，D k或C k x中的一种。输出格式
对于每个输出指令
PM，输出一个结果，表示当前集合中的最小值。每个结果占一行。
数据范围
1≤N≤105
−109≤x≤109
数据保证合法。输入样例：
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM输出样例：
-10 6
指针模拟指向的堆不常用，但在迪杰斯特拉算法里面需要用到堆，平常遇到的堆没那么复杂，要么就是用优先队列来操作。
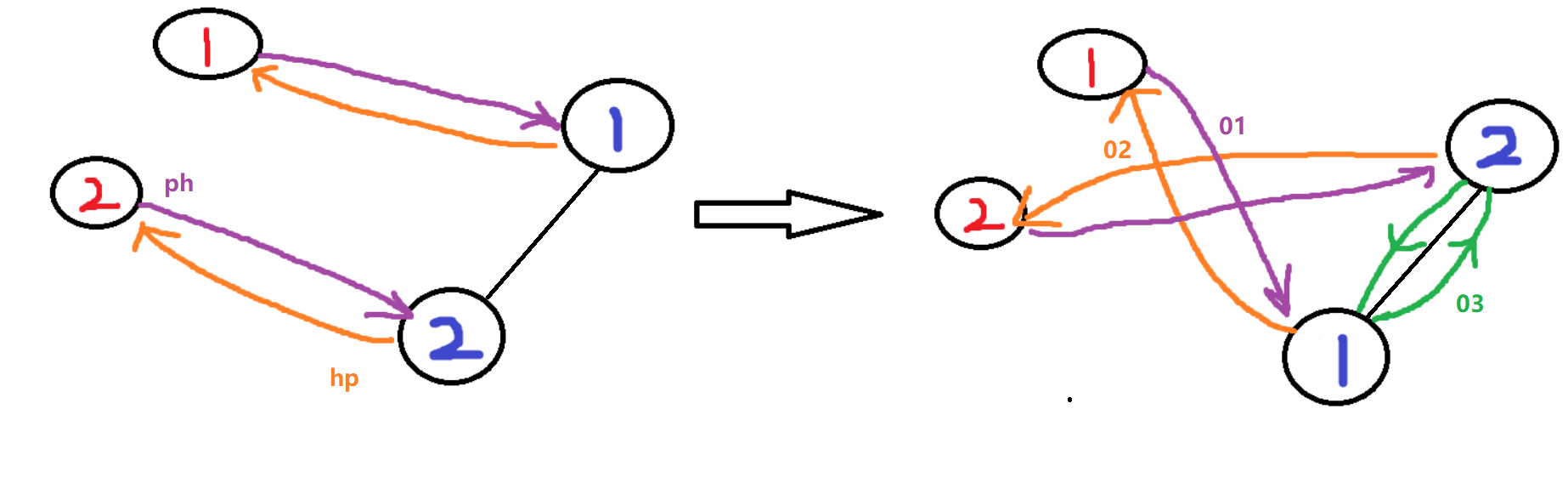
查找元素时需要知道它在当前堆中的位置在哪里，才好进行 down 或 up，所以需要hp数组（第几个插入的数字 对应 目前堆里的位置），但是单纯swap交换数字，不会改变位置指针，所以需要ph数组来用作位置指针(目前堆里的位置 对应 第几个插入的数字）
/*
* p: pointer, h: heap
* ph[]: 代表位置到堆的映射 比如：ph[k]：代表第k次插入的数 在堆的什么位置(下标)
* hp[]: 代表堆到位置的映射 比如：hp[j]：代表在堆的下标为j的元素 是第哪一次插入的
* 映射关系: 若hp[j] = k，则ph[k] = j。
*
* 为什么要有两个映射？因为，当删除或修改第k个插入的数，可能会发生交换,
* 交换的时候通过下标(hp)来找到对应的是哪一次
* 插入的数，从而维持两者的ph指向的下标(通过ph找到第k个插入元素的位置)
*/
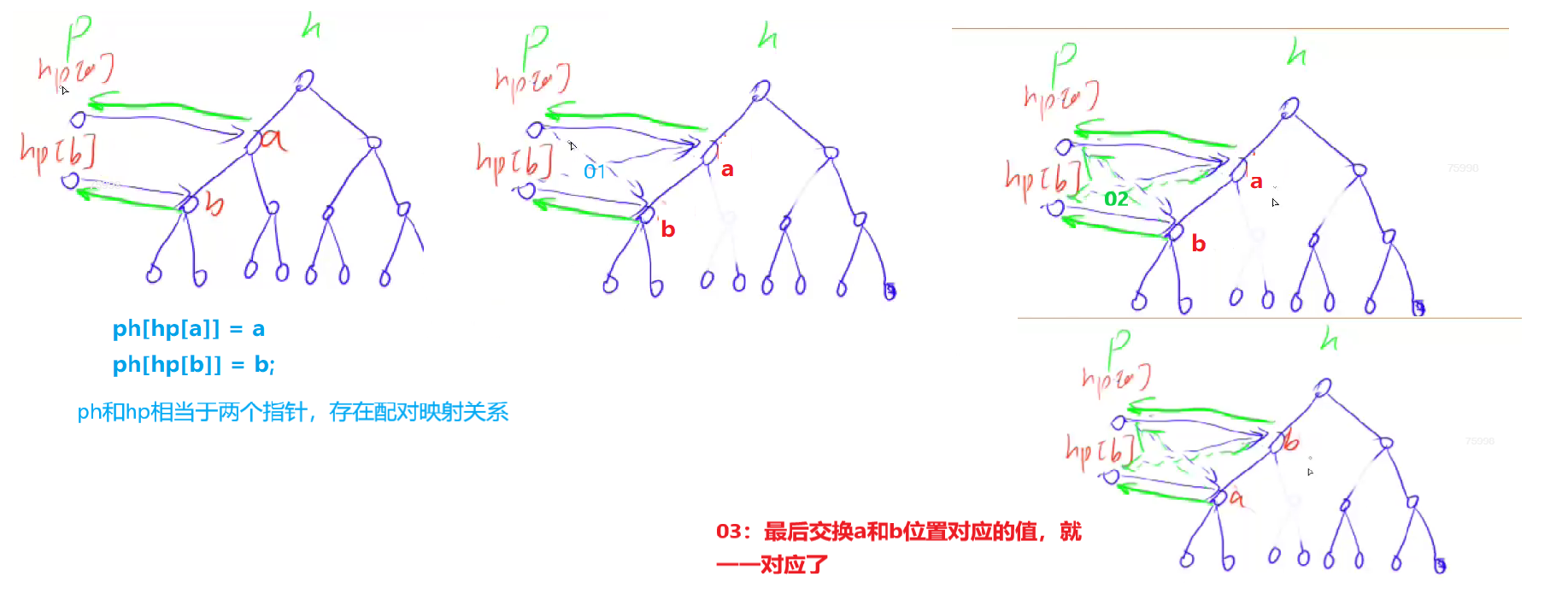
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int heap[N]; //堆
int ph[N]; //存放第k个插入点的下标
int hp[N]; //存放堆中点的插入次序
int sizes; // sizes 记录的是堆当前的数据多少
void heap_swap(int a, int b)
{
swap(ph[hp[a]], ph[hp[b]]); // 交换左指向右的指针
swap(hp[a], hp[b]); // 交换右指向左的指针
swap(heap[a], heap[b]); // 交换值
}
void down(int i)
{
int t = i;
if(2 * i <= sizes && heap[2 * i] < heap[t]) t = 2 * i;
if(2 * i + 1 <= sizes && heap[2 * i +1] < heap[t]) t = 2 * i + 1;
if(t != i)
{
heap_swap(i, t);
down(t);
}
}
void up(int i)
{
int t = i;
if(i / 2 && heap[i / 2] > heap[t]) t = i / 2;
if(t != i)
{
heap_swap(t, i);
up(t);
}
}
int main()
{
int n, m = 0; // m表示第几个插入的数
cin >> n;
while (n -- )
{
int k, x;
string opt;
cin >> opt;
if(opt == "I") // 插入一个数x：在堆的末尾位置插入
{
cin >> x;
sizes ++;
m ++;
ph[m] = sizes, hp[sizes] = m;
heap[sizes] = x;
up(sizes);
}
else if(opt == "PM") cout << heap[1] << endl;
else if(opt == "DM")
{
heap_swap(1, sizes);
sizes --;
down(1);
}
else if(opt == "D") // 删除第k个插入的数
{
cin >> k;
// 将第k次插入的元素，转换为堆中的下标
k = ph[k]; // 删除第k个插入的数，就先要找到第k个插入的数的下标（位置）
heap_swap(k, sizes);
sizes --;
down(k);
up(k);
}
else if(opt == "C")// 修改第k个插入的数
{
cin >> k >> x;
k = ph[k]; // // 修改第k个插入的数，就先要找到第k个插入的数的下标（位置）
heap[k] = x;
down(k);
up(k);
}
}
return 0;
}
部分内容参考学习：
2、acwing算法基础课
五、总结
数组模拟堆简单的操作还是比较容易理解的，但当涉及到修改和删除操作时那两个指针数组对应的映射关系就比较绕（也不常用到），多画图模拟过程，就比较好理解一些！
注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦
