DFS与BFS
DFS与BFS
dfs又称深度优先搜索,即一路走到底(一个执着的人),当走到底(到达叶子节点)时要回溯。注:回溯不是直接回到头,而是边回去边看,能不能再往下走,只有当我们明确当前节点所有的路都走不通时才回退一步!
BFS又称广度优先搜索,即一层一层的搜索,只有当每一层搜索完之后才搜索下一层(一个稳重的人)
对比:
数据结构 空间 特点
DFS : stack O(h)与高度成正比 不具有最短性
BFS: queue O(2的h次方) 具有最短性
都可以画搜索树进行理解!
DFS:
DFS即暴力搜索:最重要的是把顺序弄清楚——要以一个怎样的顺序把所有方案遍历一遍,类似于树的先序遍历
回溯键值
数字排列
如何用 dfs 解决全排列问题?
dfs 最重要的是搜索顺序。用什么顺序遍历所有方案。
对于全排列问题,以 n = 3 为例,可以这样进行搜索:
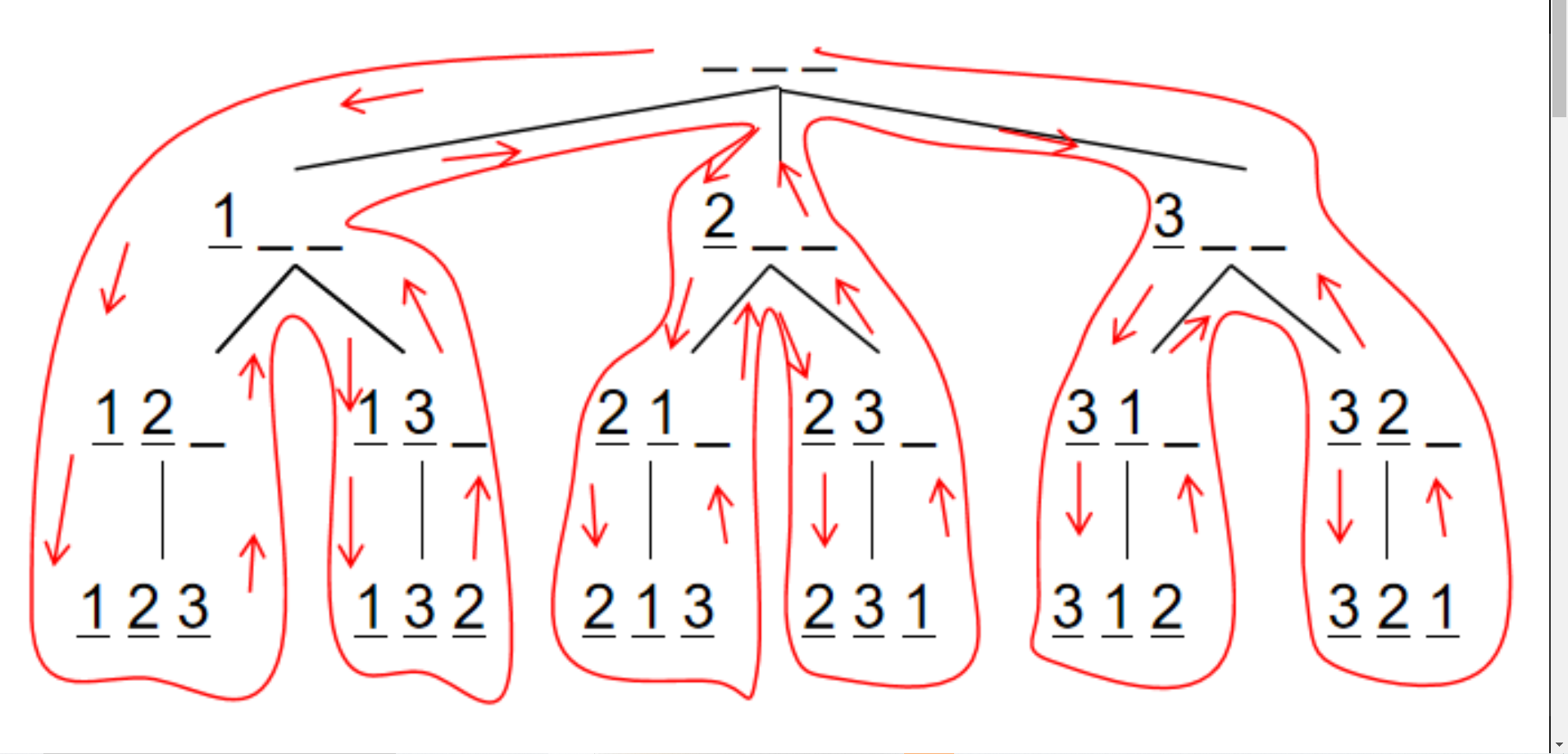
#include<iostream>
using namespace std;
const int N = 10;
int path[N];
bool vis[N];
int n;
void dfs(int u)
{
if(u == n) //到达叶子节点(数字填完了)
{
for(int i = 0; i < n; i++) cout<<path[i]<<" ";
cout<<endl;
}
// 枚举所有方案 空位上可以选择的数字为:1 ~ n
for(int i = 1; i <= n; i++)
{
if(!vis[i]) //没有被访问过
{
path[u] = i;
vis[i] = 1; // 数字被使用,状态修改
dfs(u + 1); // 填下一位
//(到达叶子节点要回溯时——恢复现场)
vis[i] = false; // 恢复现场
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
}
n皇后问题
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ){
for(int j = 0; j < n; j++){
cout<<g[i][j];
}
puts("");
}
puts(""); // 换行
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点,不再继续往下搜索)
// udg[n - u + i],+n是为了保证下标非负
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
g[u][i] = '.';
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
DFS迷宫问题(求解方案数)
无障碍物:
#include<iostream>
using namespace std;
int count,n;
bool st[100][100];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
void dfs(int x,int y){
if(x == n && y == n)
{
count ++;
return ;
}
for(int i = 0; i <= 3; i++) // 上下左右四个方向
{
int ix = x + dx[i];
int iy = y + dy[i];
if(!st[ix][iy] && ix >=1 && iy >= 1 && ix <= n && iy <= n)
{
st[ix][iy] = true;
dfs(ix, iy);
st[ix][iy] = false;
}
}
}
int main(){
cin>>n;
st[1][1] = true; // 起点标记为1
dfs(1,1);
cout<<count<<endl;
return 0;
}
#include<iostream>
using namespace std;
int count,n;
bool st[10][10];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int qx[100],qy[100];//存坐标
void dfs(int x,int y,int u){//u是第几步
if(x==n&&y==n){//结束条件
count++; // 方案数
// for(int i=0;i<u;i++){
// cout<<'('<<qx[i]<<','<<qy[i]<<')';
// }
return ;
}
for(int i=0;i<=3;i++){//枚举所有可能 情况
int ix=x+dx[i];
int iy=y+dy[i];
if(st[ix][iy]||ix<1||iy<1||ix>n||iy>n) continue;//判断当前情况是否合法 剪枝
qx[u]=ix;
qy[u]=iy;
st[ix][iy]=true;
dfs(ix,iy,u+1);
st[ix][iy]=false;//恢复现场
}
}
int main(){
cin>>n;
st[1][1]=true;//注:标记好
qx[0]=1;
qy[0]=1;
dfs(1,1,1);
cout<<count<<endl;
return 0;
}
有障碍物:

#include<iostream>
using namespace std;
bool st[100][100]; // 标记位置是否被用过
bool map[100][100]; // 标记障碍物
// 上下左右四个方向
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int count; // 计数
int n, m, t;
int sx, sy, fx, fy; // 起点终点坐标:(sx,sy)(fx,fy)
void dfs(int x,int y){
if(x == fx && y == fy)
{
count ++;
return ;
}
for(int i = 0; i <= 3; i++) // 上下左右四个方向
{
int ix = x + dx[i];
int iy = y + dy[i];
if(!st[ix][iy] && !map[ix][iy] && ix >=1 && iy >= 1 && ix <= n && iy <= m)
{
st[ix][iy] = true;
dfs(ix, iy);
st[ix][iy] = false;
}
}
}
int main(){
cin>> n>> m>> t>> sx>> sy>> fx>> fy;
while(t --) // 输入障碍物
{
int x, y;
cin>>x >> y;
map[x][y] = true; // 障碍物位置标记为1
}
st[1][1] = true; // 起点标记为1
dfs(1,1);
cout<<count<<endl;
return 0;
}
单词方阵
单词接龙
加分二叉树
虫食算
BFS
最短路问题:宽搜的优势是能找到最短(最小)路!(所有边权重都一样才可以用!)——一层一层的搜索(类似于树的层次遍历)。深搜可以保证我们走到终点,但不能确保是最短路。
搜索过程(层次遍历)如下:
(1)从图中的某个顶点出V发,访问V
(2)依次访问V的各个未曾访问过的邻接点
(3)分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问
(4)重复步骤(3)直至所有已被访问的顶点的邻接点都被访问到

图的BFS和树几乎一模一样,唯一的区别是树有根节点,而图没有,因此在遍历图时要选一个根节点。下图以A作为根节点:
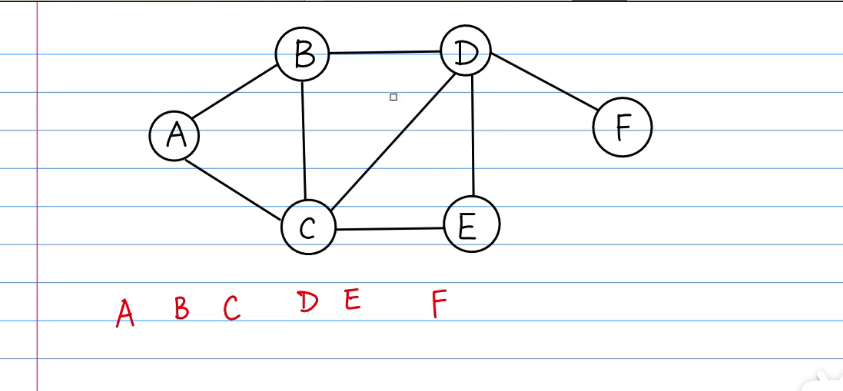
D和E是不能颠倒过来的,因为我们先遍历到的顶点是B,下一次展开的时候必须找与B直接相连的节点,即必须在找与C相连的节点之前把所有与B相连的节点找出来,由于A和C都走过了,因此唯一能走的点就是D。因此B先走完!
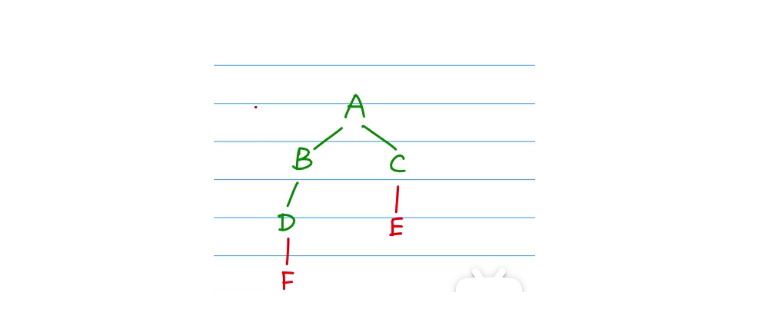
BFS的数据结构实现形式是队列,通过队列保存已被访问过的节点,利用其先进先出的特点:保证了先访问的顶点的邻接点亦先被访问
即队列保证了下图中B的邻接点比C的邻接点要先出现:
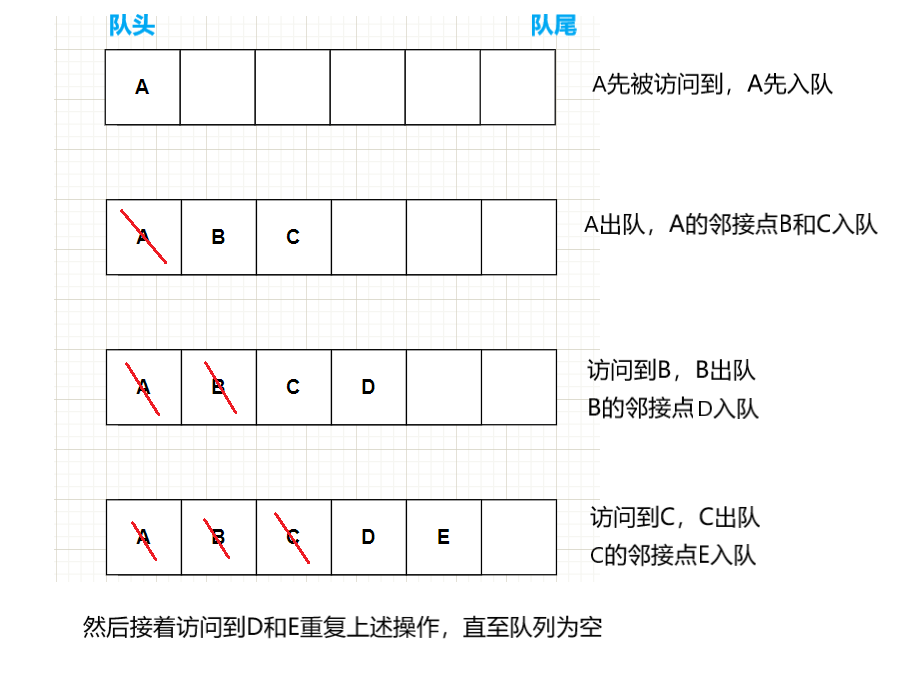
填涂颜色
马的遍历
走迷宫(acwing 844)
给定一个 n×mn×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)(n,m) 处,至少需要移动多少次。
数据保证 (1,1)(1,1) 处和 (n,m)(n,m) 处的数字为 00,且一定至少存在一条通路。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 nn 行,每行包含 mm 个整数(00 或 11),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤1001≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出样例:
8
【参考代码】
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int, int> PII; // 用pair来存储坐标
const int N = 110;
// g[N][N]初始化输入数据, d[N][N]当前位置到原点的距离
int g[N][N], d[N][N];
// 下一个节点可能的位置
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int n, m;
int bfs()
{
queue<PII> q; // 队列存储访问过的点已经该顶点的邻接点
memset(d, -1, sizeof d); // 距离初始化为- 1表示没有走过
d[0][0] = 0;
q.push({0,0}); // 开始时根节点先入队
while(q.size())
{
auto t = q.front(); // t指向队头元素(队首元素还有用)
q.pop(); // 队头元素出队
// 枚举出队的队首元素的所有邻接点
for(int i = 0; i < 4; i ++)
{
int x = t.first + dx[i];
int y = t.second + dy[i];
// d[x][y] == -1 表示该位置还没被访问过
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1; // 距离加1
q.push({x, y}); // 邻接点入队
}
}
}
// 走出迷宫返回答案
return d[n -1][m - 1];
}
int main()
{
cin>>n >>m;
// 初始化迷宫
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin>>g[i][j];
cout<<bfs();
return 0;
}
数组模拟队列:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
PII q[N * N];//手写队列
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过
d[0][0] = 0;//表示起点走过了
while(hh <= tt)//队列不空
{
PII t = q[hh ++ ];//取队头元素
for(int i = 0; i < 4; i ++ )//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
{
d[x][y] = d[t.first][t.second] + 1;//到起点的距离
q[ ++ tt ] = {x, y};//新坐标入队
}
}
}
return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
奇怪的电梯
字符串变换
机器人搬重物
memset()函数的使用
- memset()函数原型是:
extern void *memset(void *buffer, int c, int count)
//buffer:为指针或是数组,
//c:是赋给buffer的值,
//count:是buffer的长度.
这个函数在socket中多用于清空数组.如:原型是:
memset(buffer, 0, sizeof(buffer))
2.memset 用来对一段内存空间(数组)进行初始化;
int arr[N][N];
memset(arr, -1, sizeof(arr));
注:memset()可以初始化整数数组,但是初始化的值只能为0或者-1。


