单调栈与单调队列
单调栈与单调队列
单调栈就是栈内元素满足单调性的栈结构。此处的单调性分为单调递增与单调递减
如何维护一个单调栈:
单调递增栈:在保持栈内元素单调递增的前提下(如果栈顶元素大于要入栈的元素,将将其弹出),将新元素入栈。
单调递减栈:在保持栈内元素单调递减的前提下(如果栈顶元素小于要入栈的元素,则将其弹出),将新元素入栈。
什么时候使用单调栈:
给定一个序列,求序列中的每一个数左边/右边第一个比他小/比他大的数在什么地方;
注:寻找位置(下标时)stk栈存储的是下标,而不是数值
一、单调栈
1.单调递增栈
单调递增栈应用:从左往右遍历——可以找到第一个比它小的元素的位置
单调递增栈就是栈内元素满足单调递增,假设当前元素为 x ,若栈顶元素 < x ,则将 x 入栈,否则(栈顶元素 >= x)不断弹出栈顶元素,直至栈顶元素 < x 。
模板
stack<int> s;
for(int i = 1; i <= n; ++i)
{
while(s.size() && a[s.top()] >= a[i]) s.pop();
if(s.empty()) l[i] = 0;
else l[i] = s.top();
s.push(i);
}
// 数组模拟栈
for(int i = 1; i <= n ; i ++ )
{
while(tt != 0 && a[stk[tt]] >= a[i]) tt--;
if(tt == 0) l[i] = 0; // 栈为空,不存在则记为0
else l[i] = stk[tt]; // 符合要求l[i]记录对应栈顶下标
stk[++ tt] = i; // 最后当前扫描到的下标入栈
}
下面以3 1 4 5 2 7为例解释单调递增栈
【文字描述】


【动图展示】
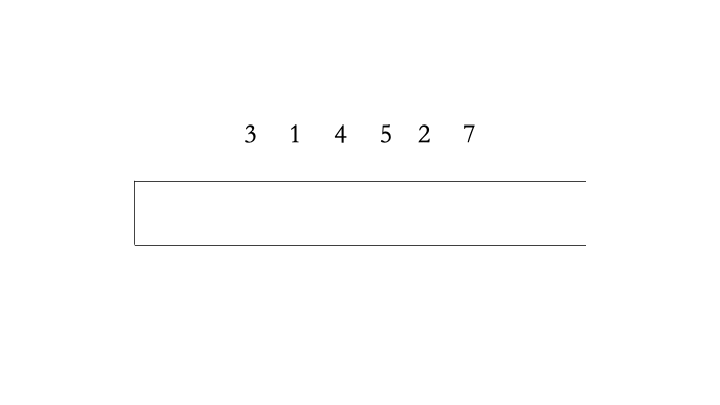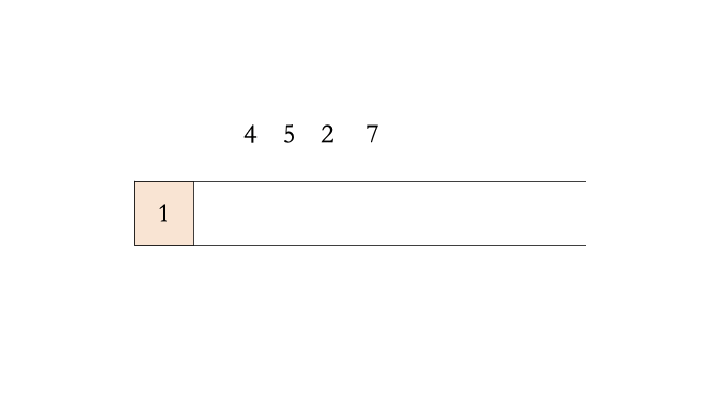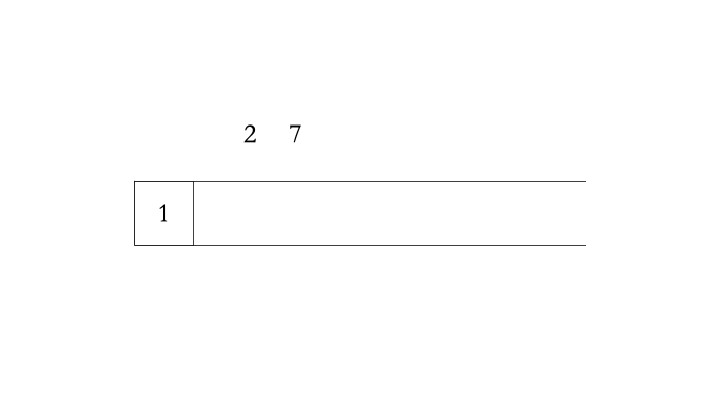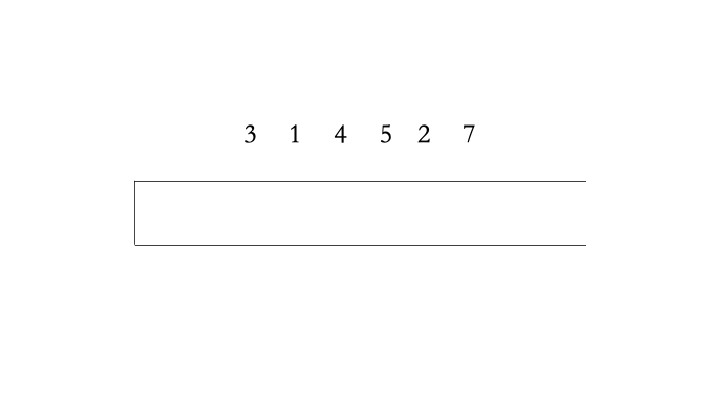 f
f
通过观察原始序列 3 1 4 5 2 7,对比结果的单调栈1 2 7可以发现 1 是 2 左边第一个小于等于它的数,稍加思考后,我们可以得知当一个数字被放入单调递增栈时,其栈内左边的数是它在原始序列中,左边第一个小于等于它的数。
【acwing 单调栈】
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 −1。
输入格式
第一行包含整数 N,表示数列长度。第二行包含 N 个整数,表示整数数列。
输出格式
共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,如果不存在则输出 −1。数据范围
1≤N≤105
1≤数列中元素≤109
输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
暴力代码:超时
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
printf("-1 ");
for (int i = 1; i < n; i++) {
for (int j = i - 1;; j--) {
if (j >= 0 && a[j] < a[i]) {
cout << a[j] << " ";
break;
} else if (j < 0) {
cout << "-1 ";
break;
}
}
}
return 0;
}
单调栈:O(n)
#include<iostream>
using namespace std;
const int N = 100000+10;
int stk[N],tt;
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++)
{
int x;
cin>>x;
while(tt != 0 && stk[tt] >= x) tt--; //如果栈顶元素大于当前待入栈元素,则出栈
if(tt == 0) cout<<"-1 "; // 栈为空(无满足要求的数)
else cout<<stk[tt]<<" "; // 满足要求输出栈顶元素
stk[++ tt] = x; // 当前元素入栈
}
return 0;
}
寻找位置:
假设有一个单调递增的栈 stk和一组数列: a = { 5 3 7 4}
用数组L[i]表示 第i个数向左遍历的第一个比它小的元素的位置
如何求L[i]?
3.1 朴素的算法 O(n^2)
可以按顺序枚举每一个数,然后再依此向左遍历。 但是当数列单调递减时,复杂度是严格的O(n^2)。
3.2 单调栈 O(n)
我们按顺序遍历数组(i : 1 -> n),然后构造一个单调递增栈。栈中存放的是元素下标,而非元素本身。
{5 3 7 4}
(1)i = 1时,因为栈为空,L[1] = 0,此时再将第一个元素的位置下标1存入栈中。
此时栈中情况:

(2)i = 2时,因当前元素a[i] = 3小于栈顶元素下标1对应的元素a[1] = 5,故将下标1弹出栈, 此时栈为空 ,故L[2] = 0 。然后将元素3对应的位置下标2存入栈中。
此时栈中情况:

(3)i = 3时,因当前元素a[i] = 7大于栈顶元素下标2对应的元素a[2] = 3,故
L[3] = stk[tt] = 2 (栈顶元素的值,说明第一个比它小的元素的下标为多少),然后将元素7对应的下标3存入栈 。
此时栈中情况:
(4)i = 4时,因当前元素a[i] =4小于栈顶元素下标3对应的元素a[3] = 7,为保持单调递增的性质,应将栈顶元素下标3弹出 ,而当前元素a[i] =4大于弹出元素后的栈顶元素下标2对应的元素a[2] = 3,不需要再继续弹出, 此时 L[4] = stk[tt] = 2;然后将元素4对应的下标4存入栈。
此时栈中情况:

(5)至此 算法结束
对应的结果:
a : 5 3 7 4
L : 0 0 2 2
下一个单调递减栈的模拟画图过程也大致同上,只不过是从后往左遍历罢了!
【将上题目答案改成寻找位置】
#include<iostream>
using namespace std;
const int N = 100000+10;
int stk[N],tt,l[N],a[N];
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
for(int i = 1; i <= n; i++)
{
while(tt != 0 && a[stk[tt]] > a[i]) tt--; //如果栈顶元素大于当前待入栈元素,则出栈
if(tt == 0) l[i] = 0; // 栈为空(无满足要求的数)
else l[i] = stk[tt]; // 满足要求输出栈顶元素
stk[++ tt] = i; // 当前元素入栈
}
for(int i = 1; i <= n; i++) cout<<l[i]<<" ";
return 0;
}
2.单调递减栈
单调递减栈应用:从右往左遍历————寻找右边第一个比当前元素大的数的位置
模板
// 单调递减栈:从右往左遍历————寻找右边第一个比当前元素大的数的位置
for(int i = n; i >= 0; i -- )
{
while(tt != 0 && a[stk[tt]] <= a[i]) tt--;
if(tt == 0) l[i] = 0; // 栈为空,不存在则记为0
else l[i] = stk[tt]; // 符合要求l[i]记录对应栈顶下标
stk[++ tt] = i; // 最后当前扫描到的下标入栈
}
【acwing 仰视奶牛】
约翰有 NN 头奶牛,编号为 11 到 NN。
现在这 NN 头奶牛按编号从小到大的顺序站成了一排,其中奶牛 ii 的身高为 HiHi。
现在,每头奶牛都向它的右侧望向那些编号较大的奶牛,对于奶牛 ii 如果存在一头奶牛 jj 满足 i<ji<j 并且 Hi<HjHi<Hj,那么我们称奶牛 ii 需要仰视奶牛 jj。
请你求出每头奶牛的最近仰视对象。
输入格式
第一行包含整数 NN。
接下来 NN 行,每行包含一个整数 HiHi,其中第 ii 行的数为编号为 ii 的奶牛的高度。
输出格式
共 NN 行,每行输出一个整数,其中第 ii 行的输出整数表示编号为 ii 的奶牛的最近仰视对象的编号,如果不存在仰视对象,则输出 00。
数据范围
1≤N≤1051≤N≤105,
1≤Hi≤1061≤Hi≤106输入样例:
6
3
2
6
1
1
2输出样例:
3
3
0
6
6
0
#include<iostream>
using namespace std;
const int N = 100000+10;
int tt, a[N], l[N], stk[N]; //stk[N]: 存储栈顶下标;l[N]记录答案
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
// 单调递减栈:从右往左遍历————寻找右边第一个比当前元素大的数的位置
for(int i = n; i >= 0; i -- )
{
while(tt != 0 && a[stk[tt]] <= a[i]) tt--;
if(tt == 0) l[i] = 0; // 栈为空,不存在则记为0
else l[i] = stk[tt]; // 符合要求l[i]记录对应栈顶下标
stk[++ tt] = i; // 最后当前扫描到的下标入栈
}
for(int i = 1; i <= n; i++) printf("%d\n", l[i]);
return 0;
}
总结
至此我们可以解答最开始的疑问,单调栈的根本作用在于求得「每一个数字在原始序列中左 / 右边第一个大于 / 小于它自身的数字或者位置」,并且由于每一个数字只会入栈一次且最多出栈一次,因此总的时间复杂度为 O ( n ) 。
一定要手动模拟画出过程图。记住:入栈操作是最后一步,别先入栈了在判断!
二、单调队列(单调双端队列)
说单调队列,那我们就先说说这个单调队列是个什么物种。单调队列从字面上看,无非就是有某种单调性的队列,没错,这就是所谓的单调队列。 单调队列它分两种,一种是单调递增的,另外一种是单调递减的。
在这搬出百度百科的解释:不断地向缓存数组里读入元素,也不时地去掉最老的元素,不定期的询问当前缓存数组里的最小的元素。
用单调队列来解决问题,一般都是需要得到当前的某个范围内(连续的字序)的最小值或最大值。
队列中元素之间的关系具有单调性,且队首和队尾都可以进行出队操作,只有队尾可以进行入队操作。
用处:
- 对于维护好的单调队列,对内元素是有序的,那么取出最大值(最小值)的复杂度为O(1)
- 可以拿来优化DP(…)
单调队列:通俗的讲就是以一个固定长度的窗口在数列上移动,(这个固定的长度是题目给的,队首元素在队列中的位置与队尾元素在队列的位置之差若大于这个固定长度,就得将队首元素弹出)
【acwing滑动窗口】
给定一个大小为n≤106 的数组。
有一个大小为 kk 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 kk 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为
[1 3 -1 -3 5 3 6 7],k 为 3。
窗口位置 最小值 最大值 [1 3 -1] -3 5 3 6 7 -1 3 1 [3 -1 -3] 5 3 6 7 -3 3 1 3 [-1 -3 5] 3 6 7 -3 5 1 3 -1 [-3 5 3] 6 7 -3 5 1 3 -1 -3 [5 3 6] 7 3 6 1 3 -1 -3 5 [3 6 7] 3 7 你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
输入样例:
8 3
1 3 -1 -3 5 3 6 7输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7

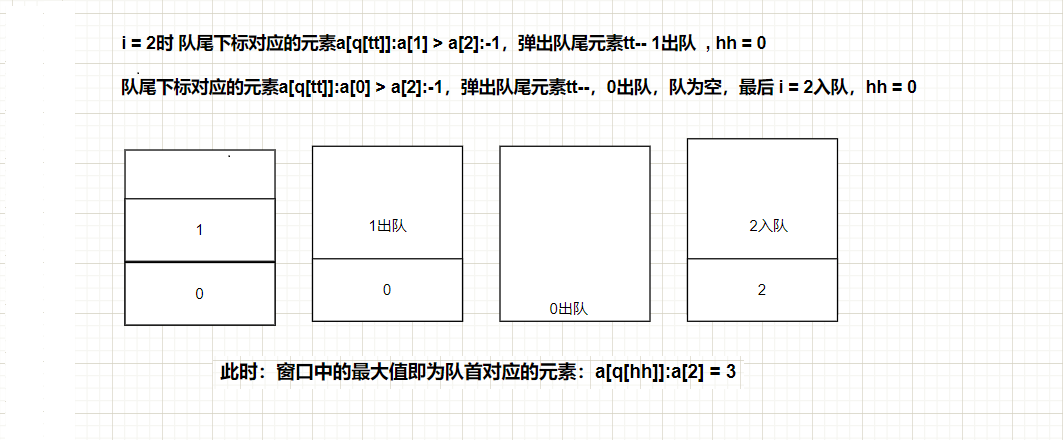
#include<iostream>
using namespace std;
const int N = 1e6 + 10; // 注意题目数组的范围
int a[N], q[N];
int main()
{
int n, k;
cin>>n >> k;
for(int i = 0; i < n; i++) cin>>a[i];
int hh = 0, tt = -1;
for(int i = 0; i < n; i++) // 暴力模拟
{
// 判断对头下标是否超出了 i - k + 1 ~ i 这个范围,若超出则去掉队头下标
// 判断是否在(i - k + 1, i)这个范围内 下标从0开始的因此要加1
if(hh <= tt && i - k + 1 > q[hh]) hh ++;
// 单调递增队列求当前区间最小值
while(hh <= tt && a[q[tt]] >= a[i]) tt --;
// 当前下下标入队
q[++ tt] = i;
//输出窗口(每个区间范围的最小值)
if(i >= k - 1) cout<< a[q[hh]]<<" ";
}
cout<<endl;
hh = 0, tt = -1; // 跟上述是对称的
for(int i = 0; i < n; i++) // 暴力模拟
{
// 判断是否滑出窗口
if(hh <= tt && i - k + 1 > q[hh]) hh ++;
// 单调递减队列求当前区间最da值
while(hh <= tt && a[q[tt]] <= a[i]) tt --;
// 当前下下标入队
q[++ tt] = i;
//输出窗口(每个区间范围的最da值)
if(i >= k - 1) cout<< a[q[hh]]<<" ";
}
return 0;
}
单调栈与单调队列总结:
(1)先用栈/队列来暴力模拟问题,即清除暴力朴素算法
(2)观察栈/队列中那些元素是没有用的,将这些没有用的数全部删掉
(3)剩下的元素具有单调性就可以进行优化
- 求极值:端点
- 找某个数——二分


