排序算法
经典排序算法
选择排序
算法思想:
A.在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
B.从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾
C.以此类推,直到所有元素均排序完毕
【参考代码】
#include<iostream>
#include<algorithm>
using namespace std;
void select_sort(int a[],int n)
{
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
if(a[i] > a[j])
{
swap(a[i],a[j]);
}
}
}
}
int main(){
int a[5] = {1,2,5,4,3};
select_sort(a,5);
for(int i = 0; i < 5; i++) cout<<a[i]<<" ";
return 0;
}
应用例题:acwing818. 数组排序
冒泡排序
1)比较相邻的元素。如果第一个比第二个大,就交换他们两个;
2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数;
3)针对所有的元素重复以上的步骤,除了最后一个;
4)持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#include<iostream>
#include<algorithm>
using namespace std;
void bubble_sort(int a[],int n)
{
for(int i = 0; i < n; i++){ // 循环的趟数
for(int j = 0; j < n - i - 1; j++){// 每一趟比较的次数
if(a[j] > a[j + 1])
{
swap(a[j],a[j + 1]);
}
}
}
}
int main(){
int a[5] = {1,2,5,4,3};
bubble_sort(a,5);
for(int i = 0; i < 5; i++) cout<<a[i]<<" ";
return 0;
}
快速排序
算法思想(分治):
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
1)确定分界点
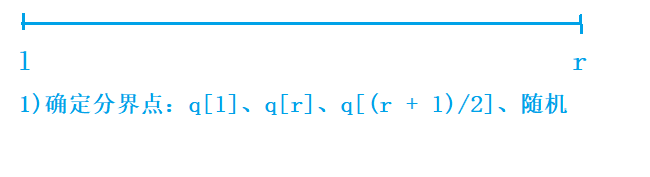
2)划分区间:使得小于等于x的在左半边,大于等于x的在右半边(防止边界问题:i = l - 1, j = r + 1)
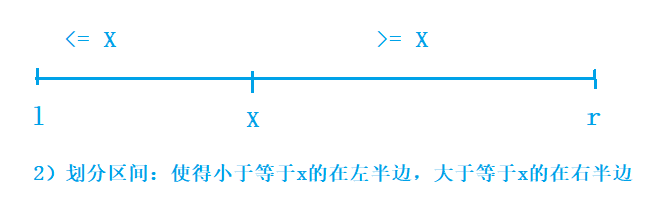
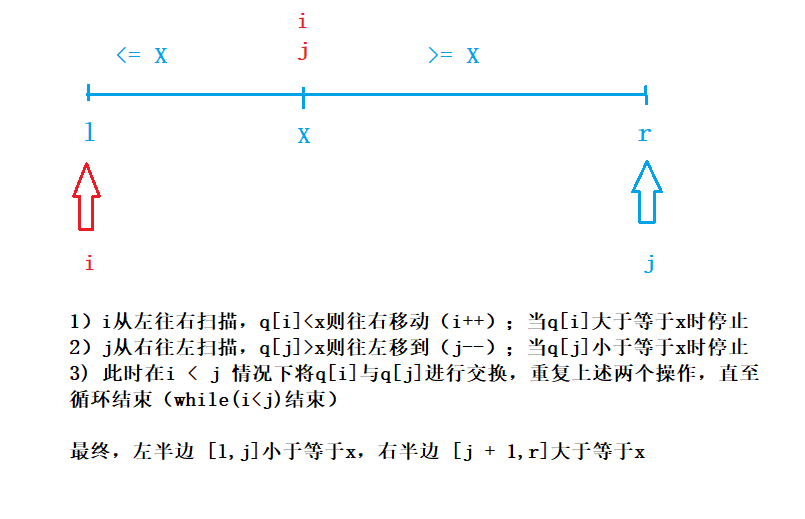
3)递归排序左右两边(最终使得整个区间有序)
【模板代码】
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int q[N];
void quick_sort(int q[], int l, int r)
{
if(l >= r) return ;
//1.确定分界点
int i = l - 1, j = r + 1;
int x = q[(l + r)/2];
//2.划分区间
while(i < j)
{
do i++; while(q[i] < x);// 当q[i]出现大于等于x时停止
do j--; while(q[j] > x);// 当q[j]出现小于等于x时停止
if(i < j) swap(q[i], q[j]);//如果两个指针还没相遇 则将上述的q[i]与q[j]交换
}
//while结束后 i==j的,边界问题下面用j更加直观
//3.递归排序左右两边
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++) cin>>q[i];
quick_sort(q, 0, n - 1);
for(int i = 0; i < n; i++) cout<<q[i]<< " ";
}
归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,归并排序对序列的元素进行逐层折半分组,然后从最小分组开始比较排序,合并成一个大的分组,逐层进行,最终所有的元素都是有序的(分治)
1)确定分界点(将整个区间一分为二):int mid = ( (l + r ) / 2)。[L,R]-->[L,mid]和[mid + 1,R](与快排不同的是归并排序的分界点取中间值
2)递归排序左右两个子区间:[ l , mid ]和[ mid + 1, r ]
3)归并,合二为一:(将两个有序的区间比较、合并(将比较的结果存到新开的数组中))

#include<iostream>
using namespace std;
const int N = 100000+10;
int q[N];
int tmp[N];
int n;
void merge_sort(int q[], int l, int r)
{
if(l >= r) return ;// 只有一个数或者没有
//1.确定分界点
int mid = (l + r)/2;
//2.递归排序左右两边
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
//3.归并,合二为一
int i = l, j = mid + 1, k = 0;
while(i <= mid && j <= r)
{
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
// 剩余部分直接添加
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
// 拿回结果
for(int i = l, j = 0; i <= r; i++, j++)q[i] = tmp[j];
}
int main()
{
cin>>n;
for(int i = 0; i < n; i++) cin>>q[i];
merge_sort(q, 0, n - 1);
for(int i = 0; i < n; i++) cout<<q[i]<<" ";
return 0;
}
求逆序对数量
给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 ii 个和第 jj 个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000,
数列中的元素的取值范围 [1,10^9]输入样例:
6 2 3 4 5 6 1输出样例:
5
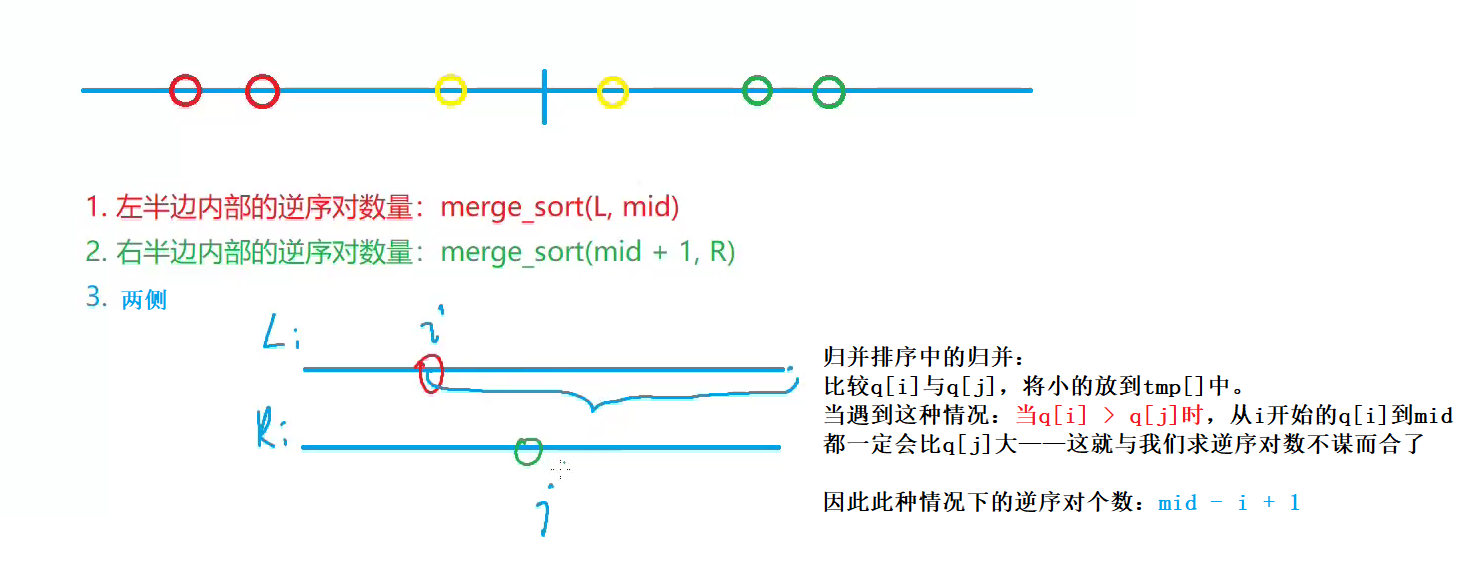
使用分治法解决问题:
我们将序列从中间分开,将逆序对分成三类:
两个元素都在左边;
两个元素都在右边;
两个元素一个在左一个在右;
因此这就是我们算法的大致框架:
计算逆序对的数量(序列):
- 递归算左边的;
- 递归算右边的;
- 算一个左一个右的;
- 把他们加到到一起。
#include<iostream>
using namespace std;
int n;
const int N = 100000+10;
int q[N],tmp[N];
typedef long long LL;
LL merge_sort(int q[], int l, int r)
{
if(l >= r) return 0;
//1.将区间一分为二
int mid = (l + r)/2;
//2.逆序对在右边或者在左边的情况
LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
//3.归并过程
int k = 0, i = l, j = mid + 1;
while(i <= mid && j <= r)
{
if(q[i] <= q[j]) tmp[k++] = q[i++];
else // 在mid两侧构成逆序对的情况
{
res += mid - i + 1;
tmp[k++] = q[j++];
}
}
//4.扫尾
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//5.物归原主
for(int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
//6.返回结果
return res;
}
int main()
{
cin>>n;
for(int i = 0; i < n; i++) cin>>q[i];
cout<<merge_sort(q,0,n-1);
return 0;
}
值得注意的是:当该序列是倒序时,逆序对个数最大 n ~1共有 (n-1 + n-2 +...+1)= n*n / 2个(5 * 10^9个)超出了
int的范围,因此,结果res用long long来记录
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
归并排序
归并排序
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11,;
逆序数为14;
合并的同时求逆序队数量
解释:在分治后的每一层合并中顺便求出逆序对数量是这个题想法的由来,归并排序分治我们求的是从小到大的顺序,我们所求的逆序对恰好是逆序数量,与归并排序不谋而合。
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else
{
res += mid - i + 1;
tmp[k ++ ] = q[j ++ ];
}
例如[3,4,1,2]中q[0]>q[2],则q[0],q[1]都与q[2]成逆序对,而q[mid]与q[i]有mid-i+1个数字,因此逆序对增加mid-i+1


