蓝桥杯——暴力枚举篇
暴力枚举
本学期学校开设了C++程序竞赛的课程，每周虽然只有一节课，但老师讲的是真的精彩，建模到映射等等思维的飞跃，还有各种excel、word解题大法，让我叹为观止！总结一些例题，希望能对自己以及想要参加蓝桥杯的你提供些许帮助！（例题、解题方法等往后会不断的更新总结！）
蛮力法：尝试每一种可能
【暴力解法】
- 确定范围
- 找出条件
- 明确输出的个数、类型、次序、格式
一般找数的题目都可以用暴力枚举
范围精确好的好——有些条件可直接放进在范围中
例题1、2013蓝桥杯——猜年龄
【题目描述】
美国数学家维纳(N.Wiener)智力早熟，11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。
一次，他参加某个重要会议，年轻的脸孔引人注目。于是有人询问他的年龄，他回答说：
“我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字，每个都恰好出现1次。”
请你推算一下，他当时到底有多年轻。
解法一：excel
思路：
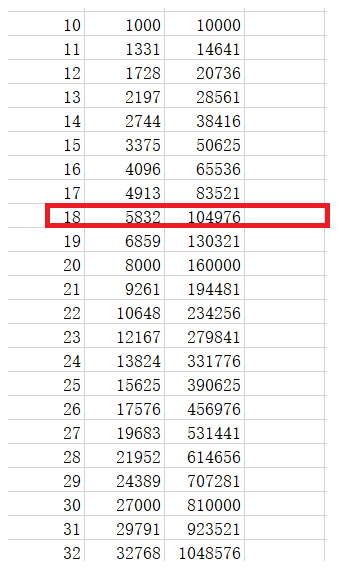
利用excel中的=POWER（）函数分别计算出1~32的立方和四次方，根据条件：这10个数字正好包含了从0到9这10个数字，每个都恰好出现1次即找到18
【解法二】
思路：
-
正常人的年龄一般0到100岁。由题意：年龄的立方是个4位数。年龄的4次方是个6位数——通过计算器可初步确认范围10到32岁之间
-
用a[10]数组来计数：记录4位数和6位数每一位中数字0~9出现的次数
-
如果 a[i]大于1则证明重复 。a[i] == 10 则成立
#include<iostream>
#include<cmath>
using namespace std;
void check(int num, int a[])
{
while(num != 0)
{
a[num % 10] ++;
num = num / 10;
}
}
int main()
{
int a[10] = {0};
int num1, num2, count = 0;
for(int x = 10; x <= 32; x++)
{
num1 = x * x * x;
if(num1 >= 1000 && num1 <= 9999){
num2 = num1 * x;
if(num2 >= 100000 && num2 <= 999999)
{
check(num1, a);
check(num2, a);
for(int i = 0; i < 10; i++)
{
if(a[i] == 1) count++;
}
}
}
if(count == 10)
{
cout << x;
break;
}
}
return 0;
}
【解法三】：STL容器set：数据不能出现重复；例如100个数中无重复——将这一百个数插入s集合中，最终集合的大小s.size()==100即表明没有重复。
#include<iostream>
#include<cmath>
#include<set>
using namespace std;
int main()
{
set<int>s;
int num1, num2;
for(int x = 10; x <= 32; x++)
{
num1 = x*x*x;
if(num1 >= 1000 && num1 <= 9999){
num2 = num1 * x;
if(num2 >= 100000 && num2 <= 999999)
{
while(num1 !=0)
{
s.insert(num1 % 10);
num1 = num1 / 10;
}
while(num2 !=0)
{
s.insert(num2 % 10);
num2 = num2 / 10;
}
}
}
if(s.size() == 10)
{
cout << x;
break;
}
}
return 0;
}
【解法四】：
- 将4位数和6位数（整数）转为字符串
- 将两个字符串拼接（10位数）
- 检查是否重复（set）
注：引入头文件：#include<set> 、#include<string>、#include<sstream>
整数转字符串方法模板：
void i2s(int num, string & str)
{
stringstream ss;
ss << num;
ss >> str;
}
【参考代码】
#include<iostream>
#include<cmath>
#include<set>
#include<string>
#include<sstream>
using namespace std;
void i2s(int num, string & str)
{
stringstream ss;
ss << num;
ss >> str;
}
bool check(string str)
{
set<char>s;// 注意：此时set是char类型
for(int i=0; i < str.length(); i++)
{
s.insert(str[i]);
}
if(str.length() == 10 && s.size() == 10) return true;
return false;
}
int main()
{
int num1, num2;
for(int x = 10; x <= 32; x++)
{
num1 = x*x*x;
num2 = num1 * x;
if(num1 >= 1000 && num1 <= 9999 && num2 >= 100000 && num2 <= 999999){
// 将整数转为字符串
string str1, str2;
i2s(num1, str1);
i2s(num2, str2);
// 4位和6位 拼接后检查
if(check(str1 + str2))
{
cout << x;
}
}
}
return 0;
}
例题2、蓝桥杯——古堡算式
【问题描述】
福尔摩斯到某古堡探险，看到门上写着一个奇怪的算式：
ABCDE * ? = EDCBA
他对华生说：“ABCDE应该代表不同的数字，问号也代表某个数字！”
华生：“我猜也是！”
于是，两人沉默了好久，还是没有算出合适的结果来。
请你利用计算机的优势，找到破解的答案。
把 ABCDE 所代表的数字写出来。
答案写在“解答.txt”中，不要写在这里！
解法：
1、枚举五个数：范围0~9
2、条件：ABCDE应该代表不同的数字 （五位数）
3、条件：ABCDE * ? = EDCBA——x*? = y --> y%x == --->得出x(五位数的才对)
#include<iostream>
using namespace std;
int main()
{ int x, y;
for(int a = 0; a < 10; a++){
for(int b = 0; b < 10 ; b++){
if( b != a)
for(int c = 0; c < 10; c++){
if( c!=a && c!=b)
for(int d = 0; d < 10 ; d++){
if( d!=a && d!=b && d!=c)
for(int e = 0; e < 10 ; e++) {
if( e!=a && e!=b && e!=c && e!=d){
x = a*10000 + b*1000 + c*100 + d*10 + e;//ABCDE
y = e*10000 + d*1000 + c*100 + b*10 + a;//EDCBA
if(y % x == 0)
{
cout << x << endl;
break;
}
}
}
}
}
}
}
return 0;
}
输出结果：
2178
4356
21978
例题3、蓝桥杯——低碳生活大奖赛
【问题描述】
某电视台举办了低碳生活大奖赛。题目的计分规则相当奇怪：
每位选手需要回答10个问题（其编号为1到10），越后面越有难度。答对的，当前分数翻倍；答错了则扣掉与题号相同的分数（选手必须回答问题，不回答按错误处理）。
每位选手都有一个起步的分数为10分。
某获胜选手最终得分刚好是100分，如果不让你看比赛过程，你能推断出他（她）哪个题目答对了，哪个题目答错了吗？
如果把答对的记为1，答错的记为0，则10个题目的回答情况可以用仅含有1和0的串来表示。例如：0010110011 就是可能的情况。
你的任务是算出所有可能情况。每个答案占一行。
思路：
- 一看到答案所给例子想到用二进制数求解
- 遍历判断二进制数1就当前分数翻倍；0就当前分数减当前题号所对应分数
由于没搞清二进制数与十进制数范围关系，一开始我遍历的是0-255（2的八次方）（8位无符号二进制数对应十进制范围）是一直没有结果的。本题是10题即十位二进制数：0~1024（2的10次方）
解题关键：要判断二进制数的每一位就显得出十进制数对应二进制数的每一位（应用：二进制数的第k位是几？（可以看本人博客位运算笔记））
例如：
int x = 10;
for(int i = 9; i >=0; i++)
{
cout << ( x >> k & 1);
}
输出结果：0 0 0 0 0 0 1 0 1 0
【参考代码】
#include<iostream>
using namespace std;
int main(){
int a[10]={10,9,8,7,6,5,4,3,2,1}; // 记录错误题目对应的扣分
int score = 10;
for(int x = 0 ; x <= 1024; x++) // 遍历所有无符号10位二进制数对应的十进制数
{
for(int i = 9; i >= 0; i --) // 将十进制数转为0、1二进制数（左到右一位一位判断）
{
if((x >> i & 1) == 1) score = 2 * score;
else if((x >> i & 1) == 0) score -= a[i];
}
if(score == 100)
{
for(int j = 9; j >= 0; j --)
cout<< (x >> j & 1)<<" ";
cout << endl;
}
score = 10; // 因为score定义的是全局变量，因此没判断完一个x就要更新
}
return 0;
}
输出结果：
0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 0 0 0 0
例题4、蓝桥杯——海盗喝酒
【问题描述】
有一群海盗（不多于20人），在船上比拼酒量。过程如下：打开一瓶酒，所有在场的人平分喝下，有几个人倒下了。再打开一瓶酒平分，又有倒下的，再次重复… 直到开了第4瓶酒，坐着的已经所剩无几，海盗船长也在其中。当第4瓶酒平分喝下后，大家都倒下了。
等船长醒来，发现海盗船搁浅了。他在航海日志中写到：“…昨天，我正好喝了一瓶…奉劝大家，开船不喝酒，喝酒别开船…”
请你根据这些信息，推断开始有多少人，每一轮喝下来还剩多少人没倒下。
如果有多个可能的答案，请列出所有答案，每个答案占一行。
格式是：人数,人数,…
例如,有一种可能是：20,5,4,2,0
多个答案排列顺序不重要。
思路：所有人平分，直到开了第4瓶酒，海盗船长也在其中，我正好喝了一瓶
-
范围：（不多于20人）：则第一轮至少为4人——a1:[4,20] a2:[3,a1) [2,a2) [1,a3)(后面三轮每一轮的人数都会比前一轮少，因为喝醉了)，当然你直接1~20也可以
-
条件：所有人平分，直到开了第4瓶酒，海盗船长也在其中，我正好喝了一瓶（1/a1 + 1/a2 + 1/a3 + 1/a4 == 1）
-
输出结果五个数，其中最后一个为0，即我们要求四个数（四轮每一轮的人数）
注：1/a1 + 1/a2 + 1/a3 + 1/a4 == 1这样使用不是很规范/整除——因此要通分
【参考代码】
#include<iostream>
using namespace std;
int main(){
for(int a1 = 4; a1 <= 20; a1++){
for(int a2 = 3; a2 < a1; a2++){
for(int a3 = 2; a3 < a2; a3++){
for(int a4 = 1; a4 < a3; a4++){
if(a2*a3*a4 + a1*a3*a4 + a1*a2*a4 + a1*a2*a3 == a1*a2*a3*a4)
{
cout<< a1 <<" "<< a2 <<" " << a3 <<" "<< a4<<" "<< "0" <<endl;
}
}
}
}
}
return 0;
}
例题5、四平方和
【问题描述】
四平方和定理，又称为拉格朗日定理：每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。
比如：5 = 0^2 + 0^2 + 1^2 + 2^2 7 = 1^2 + 1^2 + 1^2 + 2^2 （^符号表示乘方的意思）
对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开
【输入形式】例如，输入：
5
则程序应该输出：
0 0 1 2
思路：
直接暴力枚举，但如果直接四重循环0~n很可能会超时，因此必须进行优化:
1）四平方和 = n——必定有：a * a <= n、b * b <= n、c * c <= n、d * d <= n
2)要求你对4个数排序：0 <= a <= b <= c <= d——循环条件：b = a、c=b开始且最后d要>=c
3）减少循环至三重，d = sqrt(n - a * a - b * b - c * c)
【参考代码】
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
int n;
cin>> n;
for(int a = 0; a * a <= n; a++){
for(int b = a; b * b <= n; b++){
for(int c = b; c * c <= n; c++){
int d = sqrt(n - a*a - b*b - c*c);
if((d >= c) && (a*a + b*b + c*c + d*d == n))
{
cout<<a<<" "<<b<<" "<<c<<" "<<d<<endl;
}
}
}
}
return 0;
}
例题6、第100002个素数
【问题描述】
素数就是不能再进行等分的整数。比如：7，11。而9不是素数，因为它可以平分为3等份。一般认为最小的素数是2，接着是3，5，... 请问，第100002(十万零二)个素数是多少？ 请注意：2 是第一素数，3 是第二个素数，依此类推。
思路：
方法一：for暴力枚举，将所得素数存到一个数组中，从下标1开始，输出q[100002]即可
值得注意的是存储的数据可能会很庞大，因此数组要尽量开得很大，而且作为全局变量！
i的范围我找了蛮久的（10000000、10000000/2都能得出答案），而且数组的范围也要很大才行！
#include<iostream>
#include<cmath>
using namespace std;
int q[1000000]={0};
bool check(int n)
{
for(int i = 2; i <= sqrt(n); i++)
{
if(n % i == 0) return false;
}
return true;
}
int main()
{
int j = 1;
for(int i = 2 ; i<10000000/2; i++)
{
if(check(i))
{
q[j++] = i;
}
}
cout<<q[100002];
return 0;
}
方法2：为了不那么麻烦的找范围，开大范围数组，直接用while循环找答案，找到即结束！
#include<iostream>
#include<cmath>
using namespace std;
bool check(int n)
{
for(int i = 2; i<= sqrt(n); i++)
{
if(n % i == 0) return false;
}
return true;
}
int main()
{
int count = 0;
long long x = 2;
while(count != 100002 )
{
if(check(x)) count ++;
x++;
}
cout<<x - 1;
return 0;
}
注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦
