线性判别准则与线性分类编程实践
线性判别准则与线性分类编程实践
1.线性判别分析LDA总结
LDA是一种经典的降维方法线性判别分析(Linear Discriminant Analysis, 以下简称LDA)。LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用,因此我们有必要了解下它的算法原理。
1.LDA的思想
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
可能还是有点抽象,我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
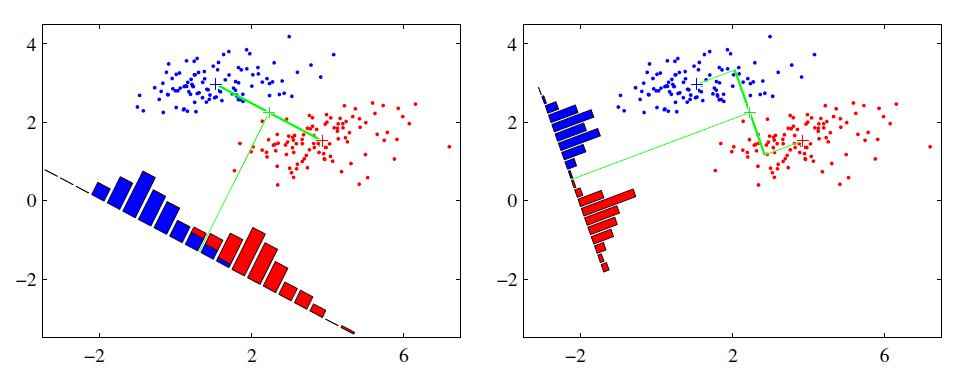
上图中国提供了两种投影方式,哪一种能更好的满足我们的标准呢?从直观上可以看出,右图要比左图的投影效果好,因为右图的黑色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了,当然在实际应用中,我们的数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
在我们将上面直观的内容转化为可以度量的问题之前,我们先了解些必要的数学基础知识,这些在后面讲解具体LDA原理时会用到。
2.瑞利商(Rayleigh quotient)与广义瑞利商(genralized Rayleigh quotient)
我们首先来看看瑞利商的定义。瑞利商是指这样的函数R(A,x)R(A,x):
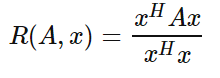
其中xx为非零向量,而AA为n×nn×n的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵,即AH=AAH=A。如果我们的矩阵A是实矩阵,则满足AT=AAT=A的矩阵即为Hermitan矩阵。
瑞利商R(A,x)R(A,x)有一个非常重要的性质,即它的最大值等于矩阵AA最大的特征值,而最小值等于矩阵AA的最小的特征值,也就是满足
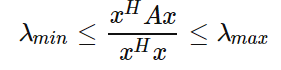
以上就是瑞利商的内容,现在我们再看看广义瑞利商。广义瑞利商是指这样的函数R(A,B,x)R(A,B,x):
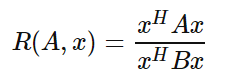
其中xx为非零向量,而A,BA,B为n×nn×n的Hermitan矩阵。BB为正定矩阵。它的最大值和最小值是什么呢?其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。我们令x=B^(−1/2)x′x=B−1/2x′,则分母转化为:
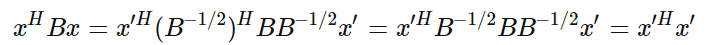
分子转化为
此时我们的R(A,B,x)R(A,B,x)转化为R(A,B,x′)R(A,B,x′):
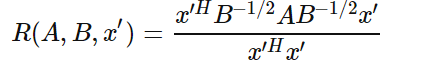
3. 二类LDA原理
现在我们回到LDA的原理上,我们在第一节说讲到了LDA希望投影后希望同一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大,但是这只是一个感官的度量。现在我们首先从比较简单的二类LDA入手,严谨的分析LDA的原理。
假设我们的数据集D={(x1,y1),(x2,y2),…,((xm,ym))},其中任意样本xi为n维向量,yi∈{0,1}。我们定义Nj(j=0,1)为第j类样本的个数,Xj(j=0,1)为第j类样本的集合,而μj(j=0,1)为第j类样本的均值向量,定义Σj(j=0,1)为第j类样本的协方差矩阵(严格说是缺少分母部分的协方差矩阵)。
μj的表达式为:
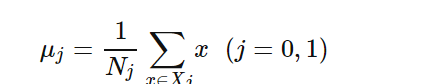
Σj的表达式为
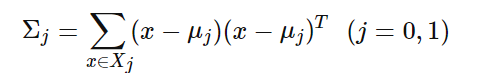
由于是两类数据,因此我们只需要将数据投影到一条直线上即可。假设我们的投影直线是向量w,则对任意一个样本本xi,它在直线w的投影为wTxi,对于我们的两个类别的中心点μ0,μ1,在在直线w的投影为wTμ0和wTμ1。由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大,也就是我们要最大化||wTμ0−wTμ1||22,同时我们希望同一种类别数据的投影点尽可能的接近,也就是要同类样本投影点的协方差wTΣ0w和wTΣ1w尽可能的小,即最小化wTΣ0w+wTΣ1w。综上所述,我们的优化目标为:
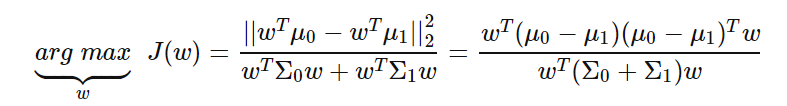
我们一般定义类内散度矩阵Sw为:
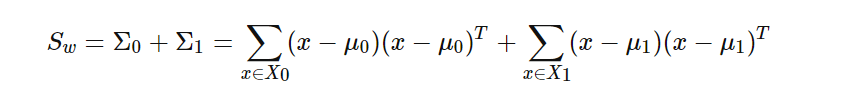
同时定义类间散度矩阵Sb为:
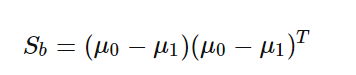
这样我们的优化目标重写为:
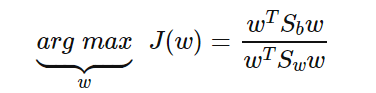
仔细一看上式,这不就是我们的广义瑞利商嘛!这就简单了,利用我们第二节讲到的广义瑞利商的性质,我们知道我们的J(w′)最大值为矩阵S−12wSbS−12w的最大特征值,而对应的w′为S−12wSbS−12w的最大特征值对应的特征向量! 而S−1wSb的特征值和S−12wSbS−12w的特征值相同,S−1wSb的特征向量w和S−12wSbS−12w的特征向量w′满足w=S−12ww′
的关系!
注意到对于二类的时候,Sbw的方向恒平行于μ0−μ1,不妨令Sbw=λ(μ0−μ1),将其带入:(S−1wSb)w=λw,可以得到w=S−1w(μ0−μ1), 也就是说我们只要求出原始二类样本的均值和方差就可以确定最佳的投影方向w了。
4.优缺点
LDA算法的主要优点有:
1)在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
2)LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
LDA算法的主要缺点有:
1)LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
2)LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3)LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
4)LDA可能过度拟合数据
2.线性分类算法(支持向量机,SVM)
1.简介
支持向量机(Support Vector Machine ,SVM)的主要思想是:建立一个最优决策超平面,使得该平面两侧距离该平面最近的两类样本之间的距离最大化,从而对分类问题提供良好的泛化能力。对于一个多维的样本集,系统随机产生一个超平面并不断移动,对样本进行分类,直到训练样本中属于不同类别的样本点正好位于该超平面的两侧,满足该条件的超平面可能有很多个,SVM正式在保证分类精度的同时,寻找到这样一个超平面,使得超平面两侧的空白区域最大化,从而实现对线性可分样本的最优分类。
支持向量机中的支持向量(Support Vector)是指训练样本集中的某些训练点,这些点最靠近分类决策面,是最难分类的数据点。SVM中最优分类标准就是这些点距离分类超平面的距离达到最大值;“机”(Machine)是机器学习领域对一些算法的统称,常把算法看做一个机器,或者学习函数。SVM是一种有监督的学习方法,主要针对小样本数据进行学习、分类和预测,类似的根据样本进行学习的方法还有决策树归纳算法等。
SVM的优点:
1、不需要很多样本,不需要有很多样本并不意味着训练样本的绝对量很少,而是说相对于其他训练分类算法比起来,同样的问题复杂度下,SVM需求的样本相对是较少的。并且由于SVM引入了核函数,所以对于高维的样本,SVM也能轻松应对。
2、结构风险最小。这种风险是指分类器对问题真实模型的逼近与问题真实解之间的累积误差。
3、非线性,是指SVM擅长应付样本数据线性不可分的情况,主要通过松弛变量(也叫惩罚变量)和核函数技术来实现,这一部分也正是SVM的精髓所在。
2.线性分类
对于最简单的情况,在一个二维空间中,要求把下图所示的白色的点和黑色的点集分类,显然,下图中的这条直线可以满足我们的要求,并且这样的直线并不是唯一的。
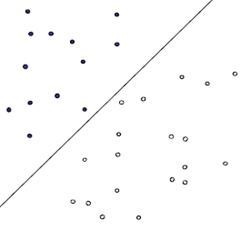
SVM的作用就是要查找到最合适的决策直线所在的位置。其他可行的直线可以如下所示:
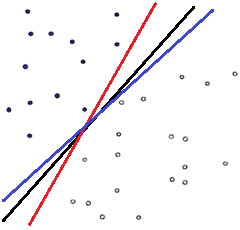
那么哪条直线才是最优的呢?就是分类两侧距离决策直线距离最近的点离该直线综合最远的那条直线,即分割的间隙越大越好,这样分出来的特征的精确性更高,容错空间也越大。这个过程在SVM中被称为最大间隔(Maximum Marginal)。下图红色和蓝色直线之间的间隙就是要最大化的间隔,显然在这种情况下,分类直线位于中间位置时可以使得最大间隔达到最大值。
2.线性不可分
现实情况中基于上文中线性分类的情况并不具有代表性,更多情况下样本数据的分布式杂乱无章的,这种情况下,基于线性分类的直线分割面就无法准确完成分割。如下图,在黑色点集中掺杂有白色点,白色点集中掺杂有黑色点的情况:
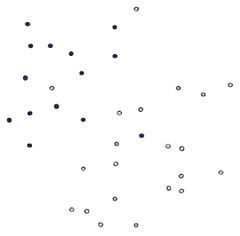
对于这种非线性的情况,一种方法是使用一条曲线去完美分割样品集,如下图:
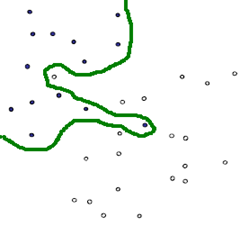
从二维空间扩展到多维,可以使用某种非线性的方法,让空间从原本的线性空间转换到另一个维度更高的空间,在这个高维的线性空间中,再用一个超平面对样本进行划分,这种情况下,相当于增加了不同样本间的区分度和区分条件。在这个过程中,核函数发挥了至关重要的作用,核函数的作用就是在保证不增加算法复杂度的情况下将完全不可分问题转化为可分或达到近似可分的状态。
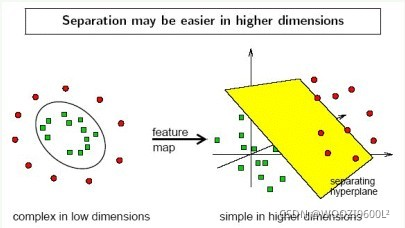
上图左侧红色和绿色的点在二维空间中,绿色的点被红色点包围,线性不可分,但是扩展到三维(多维)空间后,可以看到,红绿色点间Z方向的距离有明显差别,同种类别间的点集有一个共同特征就是他们基本都在一个面上,所以借用这个区分,可以使用一个超平面对这两类样本进行分类,如上图中黄色的平面。
线性不可分映射到高维空间,可能导致很高的维度,特殊情况下可能达到无穷多维,这种情况下会导致计算复杂,伴随产生惊人的计算量。但是在SVM中,核函数的存在,使得运算仍然是在低维空间进行的,避免了在高维空间中复杂运算的时间消耗。
SVM另一个巧妙之处是加入了一个松弛变量来处理样本数据可能存在的噪声问题,如下图所示:
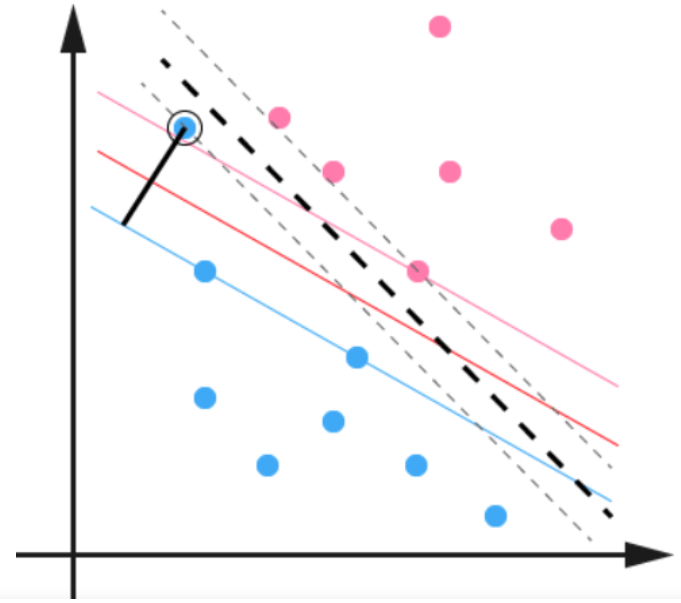
SVM允许数据点在一定程度上对超平面有所偏离,这个偏移量就是SVM算法中可以设置的outlier值,对应于上图中黑色实现的长度。松弛变量的加入使得SVM并非仅仅是追求局部效果最优,而是从样本数据分布的全局出发,统筹考量,正所谓成大事者不拘小节。
3.LDA的实现
1.鸢尾花数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
class LDA():
def Train(self, X, y):
"""X为训练数据集,y为训练label"""
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
# 求中心点
mju1 = np.mean(X1, axis=0) # mju1是ndrray类型
mju2 = np.mean(X2, axis=0)
# dot(a, b, out=None) 计算矩阵乘法
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2 = np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
# 计算w
w = np.dot(np.mat(Sw).I, (mju1 - mju2).reshape((len(mju1), 1)))
# 记录训练结果
self.mju1 = mju1 # 第1类的分类中心
self.cov1 = cov1
self.mju2 = mju2 # 第2类的分类中心
self.cov2 = cov2
self.Sw = Sw # 类内散度矩阵
self.w = w # 判别权重矩阵
def Test(self, X, y):
"""X为测试数据集,y为测试label"""
# 分类结果
y_new = np.dot((X), self.w)
# 计算fisher线性判别式
nums = len(y)
c1 = np.dot((self.mju1 - self.mju2).reshape(1, (len(self.mju1))), np.mat(self.Sw).I)
c2 = np.dot(c1, (self.mju1 + self.mju2).reshape((len(self.mju1), 1)))
c = 1/2 * c2 # 2个分类的中心
h = y_new - c
# 判别
y_hat = []
for i in range(nums):
if h[i] >= 0:
y_hat.append(0)
else:
y_hat.append(1)
# 计算分类精度
count = 0
for i in range(nums):
if y_hat[i] == y[i]:
count += 1
precise = count / nums
# 显示信息
print("测试样本数量:", nums)
print("预测正确样本的数量:", count)
print("测试准确度:", precise)
return precise
if '__main__' == __name__:
# 产生分类数据
n_samples = 500
X, y = make_classification(n_samples=n_samples, n_features=2, n_redundant=0, n_classes=2,n_informative=1, n_clusters_per_class=1, class_sep=0.5, random_state=10)
# LDA线性判别分析(二分类)
lda = LDA()
# 60% 用作训练,40%用作测试
Xtrain = X[:299, :]
Ytrain = y[:299]
Xtest = X[300:, :]
Ytest = y[300:]
lda.Train(Xtrain, Ytrain)
precise = lda.Test(Xtest, Ytest)
# 原始数据
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Test precise:" + str(precise))
plt.show()
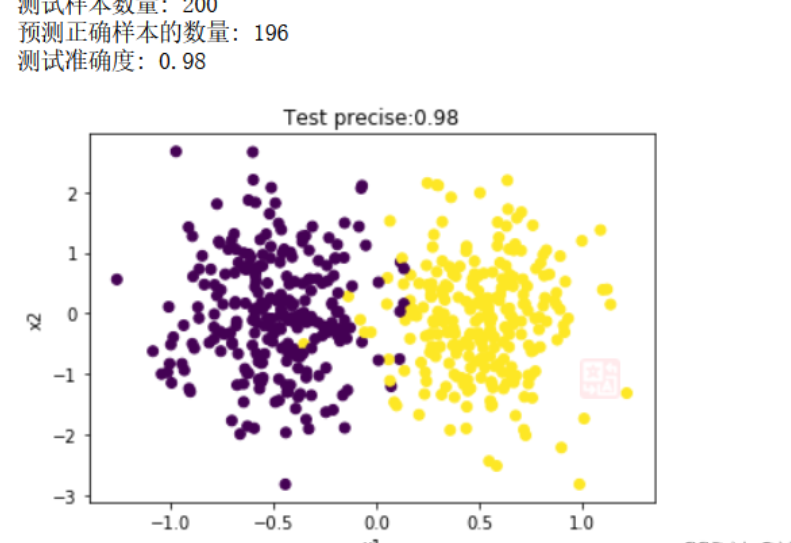
2.月亮数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
class LDA():
def Train(self, X, y):
"""X为训练数据集,y为训练label"""
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
# 求中心点
mju1 = np.mean(X1, axis=0) # mju1是ndrray类型
mju2 = np.mean(X2, axis=0)
# dot(a, b, out=None) 计算矩阵乘法
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2 = np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
# 计算w
w = np.dot(np.mat(Sw).I, (mju1 - mju2).reshape((len(mju1), 1)))
# 记录训练结果
self.mju1 = mju1 # 第1类的分类中心
self.cov1 = cov1
self.mju2 = mju2 # 第1类的分类中心
self.cov2 = cov2
self.Sw = Sw # 类内散度矩阵
self.w = w # 判别权重矩阵
def Test(self, X, y):
"""X为测试数据集,y为测试label"""
# 分类结果
y_new = np.dot((X), self.w)
# 计算fisher线性判别式
nums = len(y)
c1 = np.dot((self.mju1 - self.mju2).reshape(1, (len(self.mju1))), np.mat(self.Sw).I)
c2 = np.dot(c1, (self.mju1 + self.mju2).reshape((len(self.mju1), 1)))
c = 1/2 * c2 # 2个分类的中心
h = y_new - c
# 判别
y_hat = []
for i in range(nums):
if h[i] >= 0:
y_hat.append(0)
else:
y_hat.append(1)
# 计算分类精度
count = 0
for i in range(nums):
if y_hat[i] == y[i]:
count += 1
precise = count / (nums+0.000001)
# 显示信息
print("测试样本数量:", nums)
print("预测正确样本的数量:", count)
print("测试准确度:", precise)
return precise
if '__main__' == __name__:
# 产生分类数据
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
# LDA线性判别分析(二分类)
lda = LDA()
# 60% 用作训练,40%用作测试
Xtrain = X[:60, :]
Ytrain = y[:60]
Xtest = X[40:, :]
Ytest = y[40:]
lda.Train(Xtrain, Ytrain)
precise = lda.Test(Xtest, Ytest)
# 原始数据
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Test precise:" + str(precise))
plt.show()
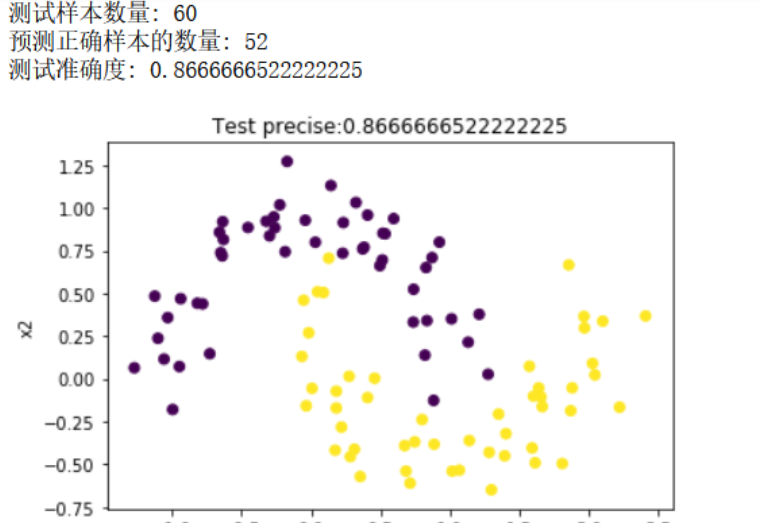
4、SVM处理月亮数据集
1.线性核分析
导入月亮数据集和svm方法:
#
#这是线性svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子,nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别,并且只取前两个特征
plt.show()
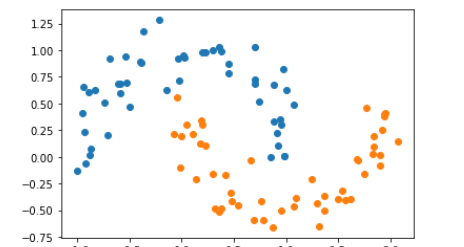
可以发现月亮数据集是交织在一起的两条弧线
scaler=StandardScaler()# 标准化
scaler.fit(data_x)#计算训练数据的均值和方差
data_x=scaler.transform(data_x) #再用scaler中的均值和方差来转换X,使X标准化
liner_svc=LinearSVC(C=1e9,max_iter=100000)#线性svm分类器,iter是迭达次数,c值决定的是容错,c越大,容错越小
liner_svc.fit(data_x,data_y)
# 边界绘制函数
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
# meshgrid函数是从坐标向量中返回坐标矩阵
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new)#获取预测值
zz=y_predict.reshape(x0.shape)
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,zz,cmap=custom_cmap)
#画图并显示参数和截距
plot_decision_boundary(liner_svc,axis=[-3,3,-3,3])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(liner_svc.coef_)
print('模型截距')
print(liner_svc.intercept_

可以看到这种情况下线性svm效果并不好。
2.多项式核分析
# 导入月亮数据集和svm方法
#这是多项式核svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from sklearn.pipeline import Pipeline #导入python里的管道
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子,nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别,并且只取前两个特征
plt.show()
def PolynomialSVC(degree,c=10):#多项式svm
return Pipeline([
# 将源数据 映射到 3阶多项式
("poly_features", PolynomialFeatures(degree=degree)),
# 标准化
("scaler", StandardScaler()),
# SVC线性分类器
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42,max_iter=10000))
])
# 进行模型训练并画图
poly_svc=PolynomialSVC(degree=3)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(poly_svc.named_steps['svm_clf'].coef_)
print('模型截距')
print(poly_svc.named_steps['svm_clf'].intercept_)
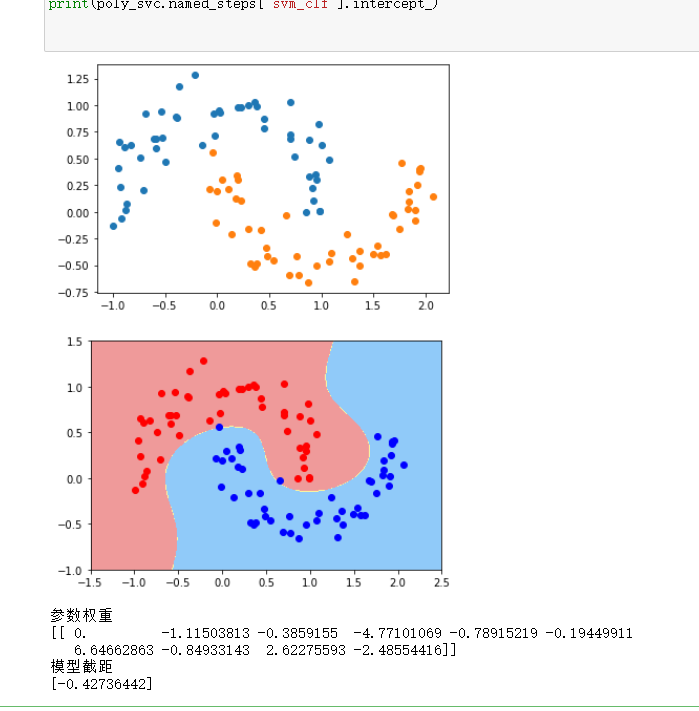
3.高斯核
gamma=1
## 导入包
from sklearn import datasets #导入数据集
from sklearn.svm import SVC #导入svm
from sklearn.pipeline import Pipeline #导入python里的管道
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler#导入标准化
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
svc=RBFKernelSVC(gamma=1)#gamma参数很重要,gamma参数越大,支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()

gamma=10
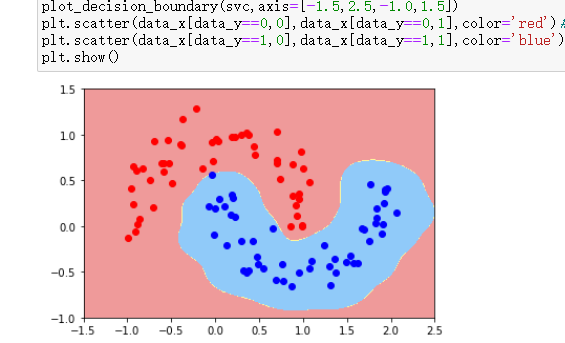
gamma=100
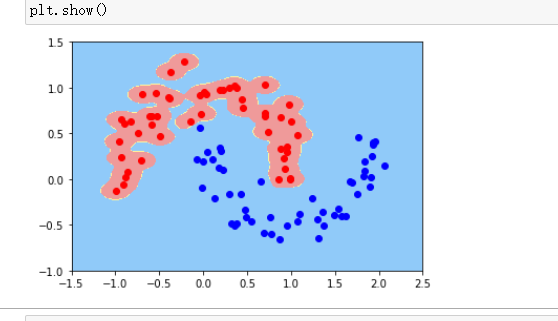
当参数gamma的值设置的特别大的时候,模型容易出现过拟合的结果,适当的调整gamma的大小,可以得到最优的模型。
5、总结
LDA算法既可以用来降维,又可以用来分类,但是目前来说,主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时,LDA是一个有力的工具。SVM则是求出分界线附近的支持向量,通过支持向量来确认分界线
参考学习了以下大神的博客
https://www.cnblogs.com/pinard/p/6244265.html
https://blog.csdn.net/dcrmg/article/details/53000150
https://blog.csdn.net/weixin_46129506/article/details/121071181
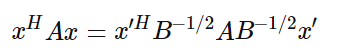

 浙公网安备 33010602011771号
浙公网安备 33010602011771号