人工智能与机器学习(1)——初识线性回归
人工智能与机器学习(1)——初识线性回归
目录
一.用excel中数据分析功能做线性回归练习
1.选取前二十,两百,两千组数据生成散点图,再点击任意一个点,右键添加趋势线选择线性并选择显示公式。
二.通过jupyter进行python编程实现线性回归练习
通过python实现最小二乘法对数据进行拟合初步了解学习线性回归
1.不借助第三方库使用最小二乘法对数据进行拟合
import numpy as np
import pandas
import xlrd
import matplotlib.pyplot as plt
首先引入数据处理所需要的包
#导入需要读取Excel表格的路径
data = xlrd.open_workbook("weights_heights.xls")
table = data.sheets()[1]
x=[]
y=[]
for i in range (1,5000):
x.append(table.cell(i,1).value)
y.append(table.cell(i,2).value)
将表格中数据存入到数组之中
plt.scatter(x[0:200], y[0:200])
plt.show()
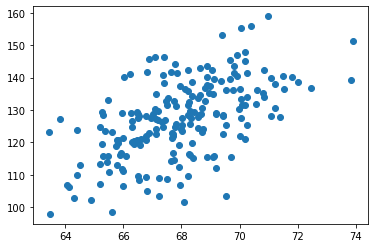
使用前两百组数据画出散点图

通过上课学习得知通过最小二乘法所得到的线性回归方程参数为上图所示
def f(a):
sum=0
pingjunx=0
pingjuny=0
chu=0
for i in range(0,a):
pingjunx+=x[i]
pingjuny+=y[i]
pingjuny/=a
pingjunx/=a
for i in range(0,a):
sum+=(x[i]-pingjunx)*(y[i]-pingjuny)
chu+=(x[i]-pingjunx)*(x[i]-pingjuny)
B1=sum/chu
B0=pingjuny-B1*pingjunx
print(B1)
print(B0)
xx = np.linspace(0,100, 100)
yy = B1*xx+B0
plt.scatter(x[0:a], y[0:a],s = 1)
plt.xlim(62,74)
plt.ylim(0,180)
print("相关系数R^2为")
shang=0
xia1=0
xia2=0
for i in range (0,a):
xia1+=(x[i]-pingjunx)*(x[i]-pingjunx)
xia2+=(y[i]-pingjuny)*(y[i]-pingjuny)
shang+=(x[i]-pingjunx)*(y[i]-pingjuny)
print(shang*shang/(xia1*xia2))
plt.plot(xx, yy, c='orange')
plt.show()
return
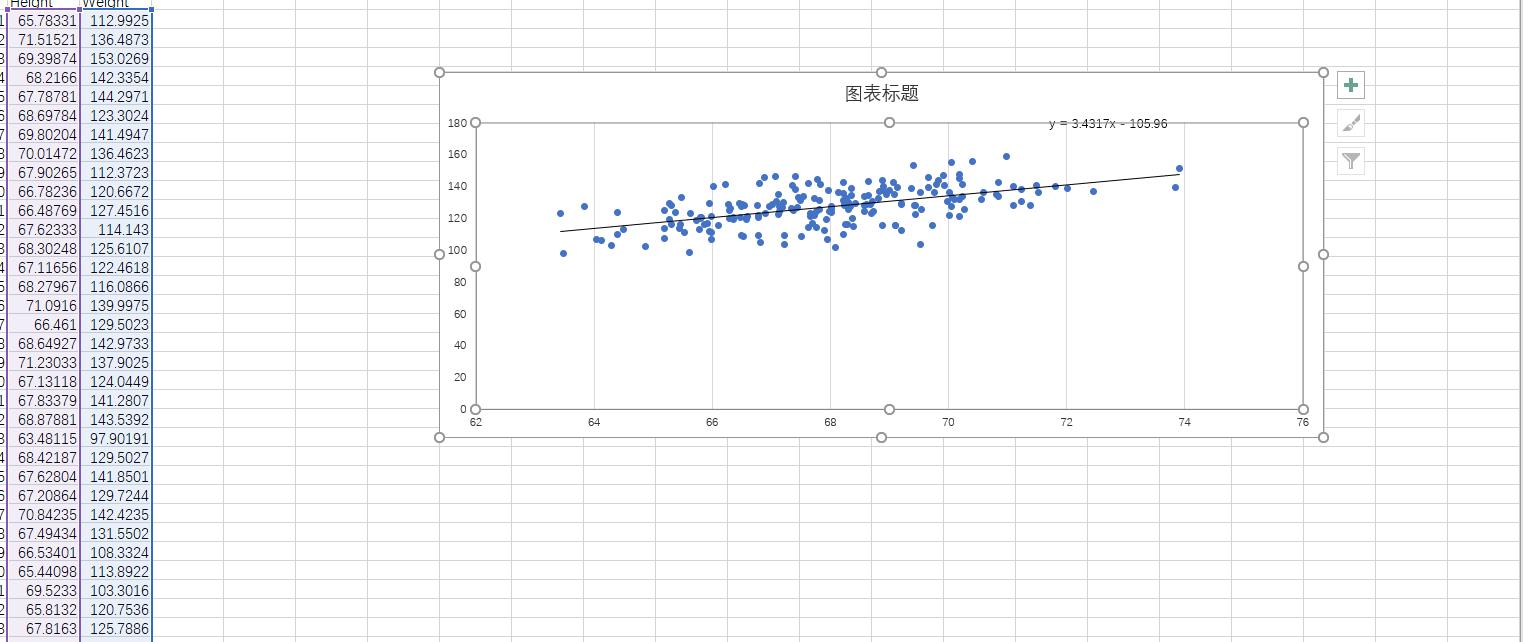
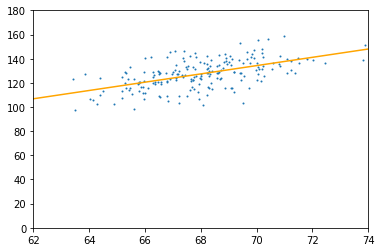
如下图所示是取前两百个数组时所得到的线性回归方程y=3.431665151629877*x-105.95901104669866 相关系数为0.30999553433092275
f(200)
3.431665151629877
-105.95901104669866
相关系数R^2为
0.30999553433092275
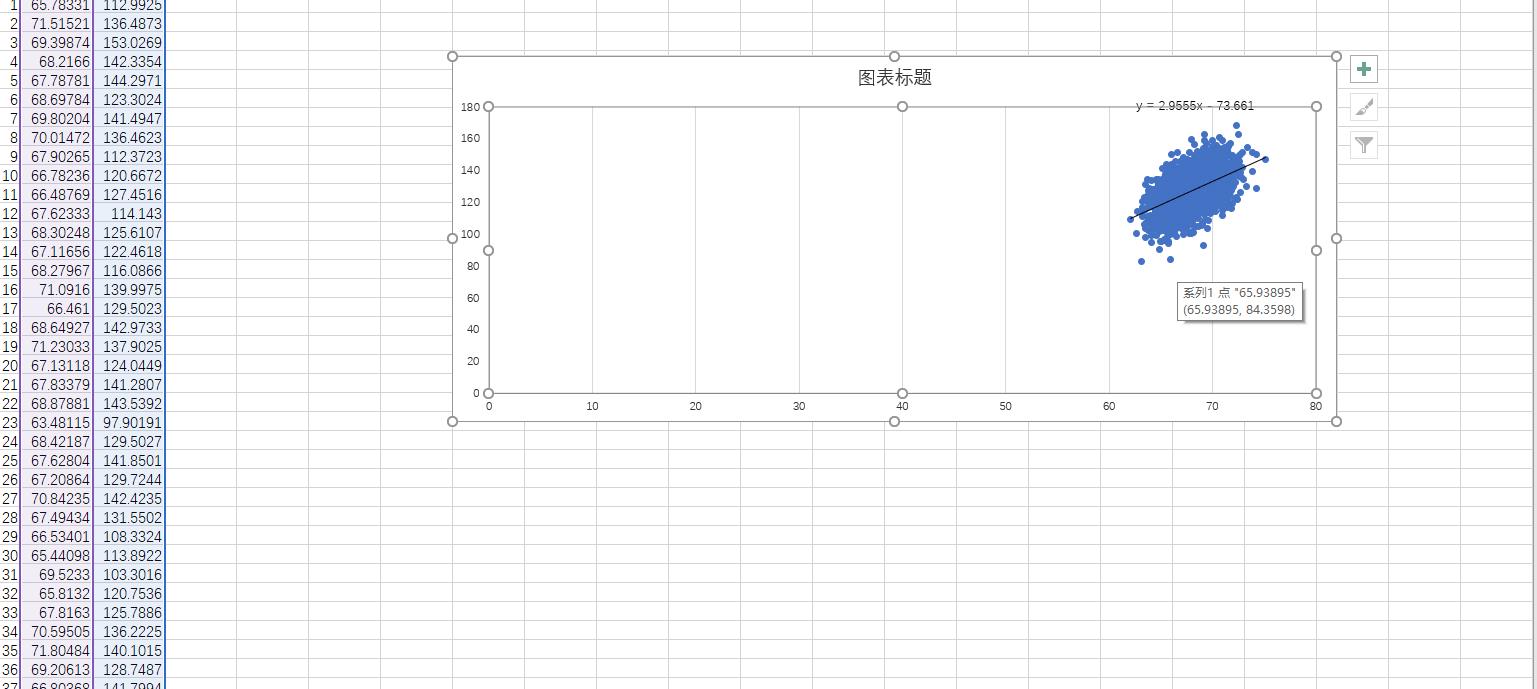
f(2000)
2.955526969810711
-73.66078552357604
相关系数R^2为
0.2483012033638441
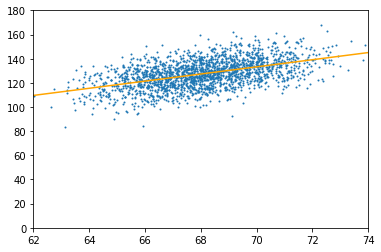
如下图所示是取前两千个数时所得到的线性回归方程y=2.955526969810711*x-73.66078552357604 相关系数为0.2483012033638441
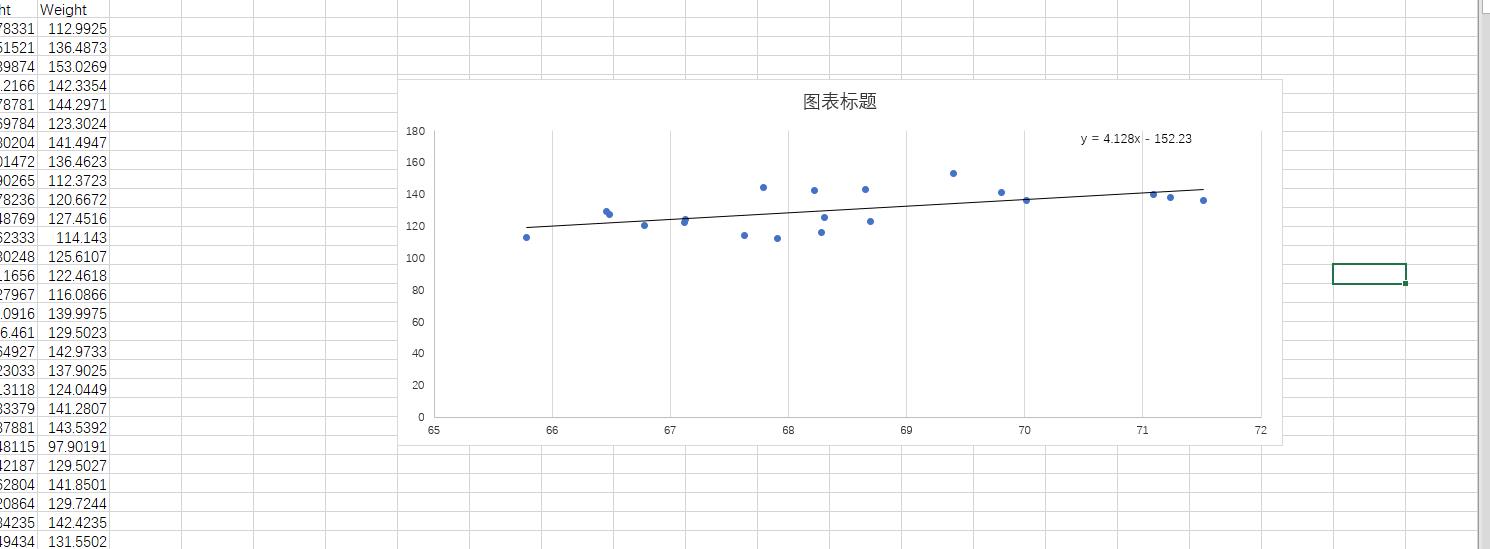
f(20)
4.128037498887677
-152.23378453438318
相关系数R^2为
0.32542302493662534
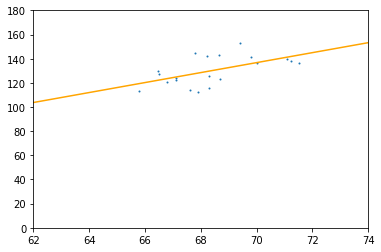
如下图所示是取前二十个数时所得到的线性回归方程y=4.128037498887677*x-152.23378453438318 相关系数为0.32542302493662534
2.借助skleran对数据进行拟合
from sklearn import linear_model
引入所需要的包
def ff(a):
model = linear_model.LinearRegression()
model.fit(np.array(x[0:a]).reshape(-1, 1),np.array(y[0:a]).reshape(-1, 1))
print(model.coef_)
print(model.intercept_)
通过sklearn中的api创建一个线性回归模型,选取a个数据进行拟合输出截距以及斜率
ff(20)
[[4.1280375]]
[-152.23378453]
ff(200)
[[3.43166515]]
[-105.95901105]
ff(2000)
[[2.95552697]]
[-73.66078552]
可以看到sklearn他的一元线性回归方程也是通过最小二乘法来实现以至于得到了同样的结果

