VAE大总结
VAE大总结
三篇文章均转自苏剑林苏神的文章,其个人主页在此
(一) VAE慢谈
这一部分我们先回顾一般教程是怎么介绍 VAE 的,然后再探究有什么问题,接着就自然地发现了 VAE 真正的面目。
经典回顾
首先我们有一批数据样本 {X1,…,Xn},其整体用 X 来描述,我们本想根据 {X1,…,Xn} 得到 X 的分布 p(X),如果能得到的话,那我直接根据 p(X) 来采样,就可以得到所有可能的 X 了(包括 {X1,…,Xn} 以外的),这是一个终极理想的生成模型了。
当然,这个理想很难实现,于是我们将分布改一改:
这里我们就不区分求和还是求积分了,意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X 的模型,而我们假设 Z 服从标准正态分布,也就是 p(Z)=N(0,I)。如果这个理想能实现,那么我们就可以先从标准正态分布中采样一个 *Z*,然后根据 *Z* 来算一个 *X*,也是一个很棒的生成模型。
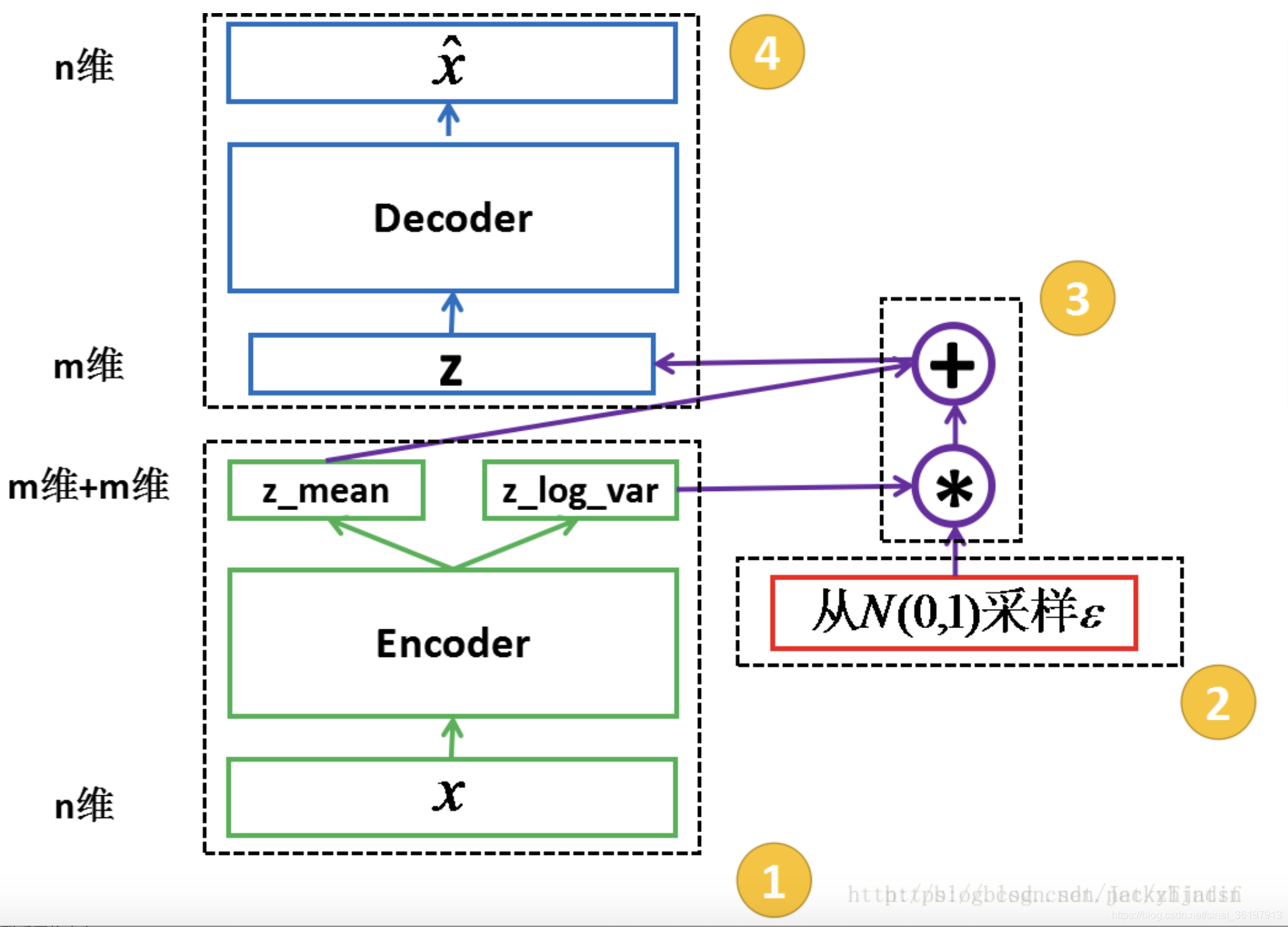
接下来就是结合自编码器来实现重构,保证有效信息没有丢失,再加上一系列的推导,最后把模型实现。框架的示意图如下:
▲ VAE的传统理解
看出了什么问题了吗?如果像这个图的话,我们其实完全不清楚:究竟经过重新采样出来的 Zk,是不是还对应着原来的 Xk,而事实上你看代码也会发现根本不是这样实现的。
VAE初现
其实,在整个 VAE 模型中,我们并没有去使用 p(Z)(先验分布)是正态分布的假设,我们用的是假设 p(Z|X)(后验分布)是正态分布。
具体来说,给定一个真实样本 Xk,我们假设存在一个专属于Xk的分布p(Z|Xk)(学名叫后验分布),并进一步假设这个分布是(独立的、多元的)正态分布。
为什么要强调“专属”呢?因为我们后面要训练一个生成器 X=g(Z),希望能够把从分布 p(Z|Xk) 采样出来的一个 Zk 还原为 Xk。
如果假设 p(Z) 是正态分布,然后从 p(Z) 中采样一个 Z,那么我们怎么知道这个 Z 对应于哪个真实的 X 呢?现在 p(Z|Xk) 专属于 Xk,我们有理由说从这个分布采样出来的Z应该要还原到 Xk 中去。
再次强调,这时候每一个 Xk 都配上了一个专属的正态分布,才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数:均值 μ 和方差 σ^2(多元的话,它们都是向量)。
那我怎么找出专属于 Xk的正态分布p(Z|Xk) 的均值和方差呢?好像并没有什么直接的思路。
那好吧,我就用神经网络来拟合出来。这就是神经网络时代的哲学:难算的我们都用神经网络来拟合,在 WGAN 那里我们已经体验过一次了,现在再次体验到了。
于是我们构建两个神经网络 μk=f1(Xk),logσ^2=f2(Xk) 来算它们了。我们选择拟合 logσ^2 而不是直接拟合 σ^2,是因为 σ^2 总是非负的,需要加激活函数处理,而拟合 logσ^2 不需要加激活函数,因为它可正可负。
到这里,我能知道专属于 Xk 的均值和方差了,也就知道它的正态分布长什么样了,然后从这个专属分布中采样一个 Zk 出来,然后经过一个生成器得到 X̂k=g(Zk)。
现在我们可以放心地最小化 D(X̂k,Xk)^2,因为 Zk 是从专属 Xk 的分布中采样出来的,这个生成器应该要把开始的 Xk 还原回来。于是可以画出 VAE 的示意图:
事实上,VAE 是为每个样本构造专属的正态分布,然后采样来重构。
分布标准化
让我们来思考一下,根据上图的训练过程,最终会得到什么结果。
首先,我们希望重构 X,也就是最小化 D(X̂k,Xk)^2,但是这个重构过程受到噪声的影响,因为 Zk 是通过重新采样过的,不是直接由 encoder 算出来的。
显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。
而方差为 0 的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。
说白了,模型会慢慢退化成普通的 AutoEncoder,噪声不再起作用。
这样不就白费力气了吗?说好的生成模型呢?
别急别急,其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。
怎么理解“保证了生成能力呢?如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I),那么根据定义:
这样我们就能达到我们的先验假设:p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。
为了使模型具有生成能力,VAE 要求每个 p(Z|X) 都向正态分布看齐。
那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢?如果没有外部知识的话,其实最直接的方法应该是在重构误差的基础上中加入额外的 loss:
因为它们分别代表了均值 μk 和方差的对数 logσ^2,达到 N(0,I) 就是希望二者尽量接近于 0 了。不过,这又会面临着这两个损失的比例要怎么选取的问题,选取得不好,生成的图像会比较模糊。
所以,原论文直接算了一般(各分量独立的)正态分布与标准正态分布的 KL 散度 KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss,计算结果为:
这里的 d 是隐变量 Z 的维度,而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss,就不用考虑均值损失和方差损失的相对比例问题了。
显然,这个 loss 也可以分两部分理解:
本质是什么
VAE 的本质是什么?VAE 虽然也称是 AE(AutoEncoder)的一种,但它的做法(或者说它对网络的诠释)是别具一格的。
在 VAE 中,它的 Encoder 有两个,一个用来计算均值,一个用来计算方差,这已经让人意外了:Encoder 不是用来 Encode 的,是用来算均值和方差的,这真是大新闻了,还有均值和方差不都是统计量吗,怎么是用神经网络来算的?
事实上,我觉得 VAE 从让普通人望而生畏的变分和贝叶斯理论出发,最后落地到一个具体的模型中,虽然走了比较长的一段路,但最终的模型其实是很接地气的。
它本质上就是在我们常规的自编码器的基础上,对 encoder 的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果 decoder 能够对噪声有鲁棒性****;而那个额外的 KL loss(目的是让均值为 0,方差为 1),事实上就是相当于对 encoder 的一个正则项,希望 encoder 出来的东西均有零均值。
那另外一个 encoder(对应着计算方差的网络)的作用呢?它是用来动态调节噪声的强度的。
直觉上来想,当 decoder 还没有训练好时(重构误差远大于 KL loss),就会适当降低噪声(KL loss 增加),使得拟合起来容易一些(重构误差开始下降)。
反之,如果 decoder 训练得还不错时(重构误差小于 KL loss),这时候噪声就会增加(KL loss 减少),使得拟合更加困难了(重构误差又开始增加),这时候 decoder 就要想办法提高它的生成能力了。
▲ VAE的本质结构
说白了,重构的过程是希望没噪声的,而 KL loss 则希望有高斯噪声的,两者是对立的。所以,VAE 跟 GAN 一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。
(二) VAE:变分自编码器
相比于自编码器,VAE更倾向于数据生成。只要训练好了decoder,我们就可以从标准正态分布生成数据作为解码器的输入,来生成类似但不同于训练数据的新样本,作用类似GAN。
实际上,在AE的基础上通过encoder产生的向量,可以这么理解:
假如在AE中,一张满月的图片作为输入,模型得到的输出是一张满月的图片;一张弦月的图片作为输入,模型得到的是一张弦月的图片。当从满月的code和弦月的code中间sample出一个点,我们希望是一张介于满月和弦月之间的图片,但实际上,对于AE我们没办法确定模型会输出什么样的图片,因为我们并不知道模型从满月的code到弦月的code发生了什么变化。
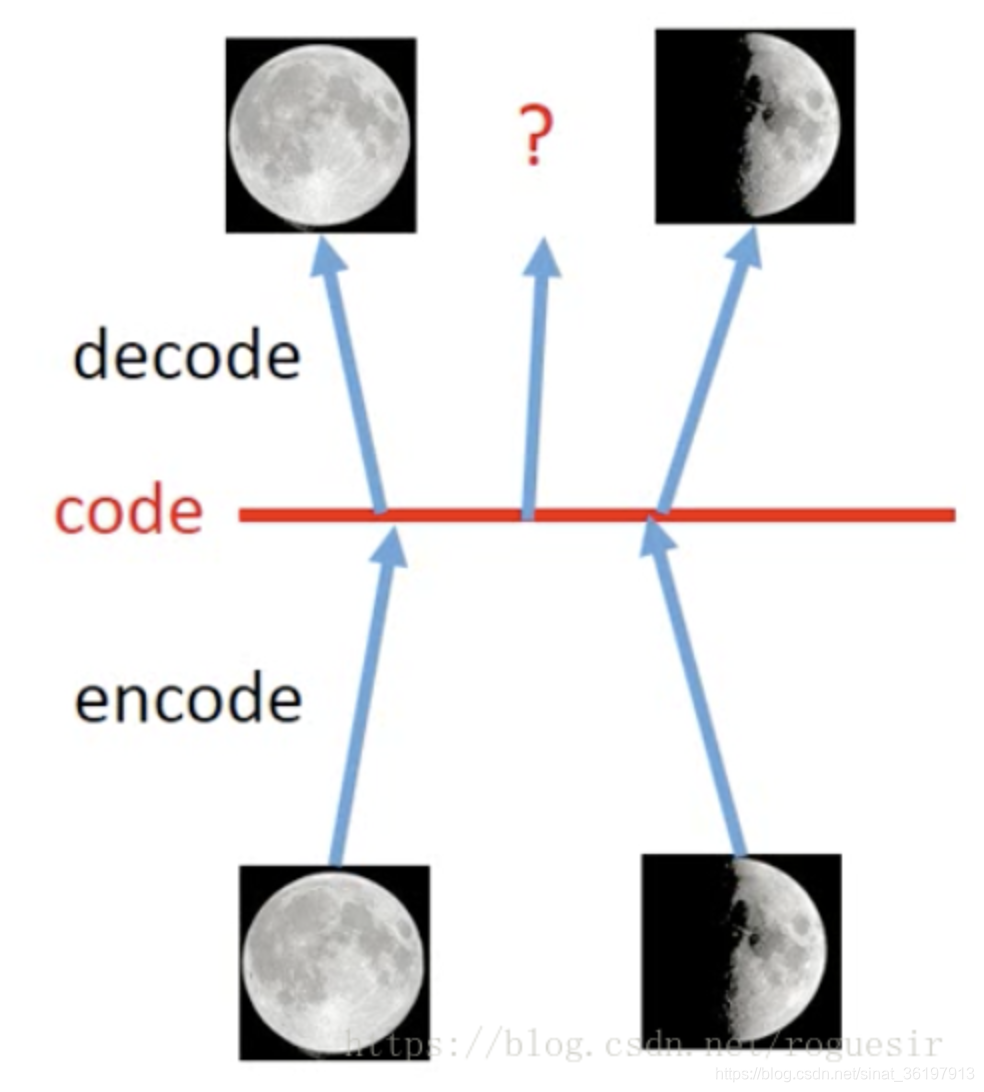
而VAE做的事情,实际上就是在原本满月和弦月生成的code上面加了noise,即在某个数值区间内,每个点理论上都可以输出满月的图片;在某个数值区间内,每个点理论上都可以输出弦月的图片,当调整这个noise的值的时候,也就是改变了这个数值区间,如下图所示,当两个区间出现重合的公共点,那么理论上,这个点既应该像满月,又应该像弦月,因此输出的图片就应该兼具满月和弦月的图片特点,也就生成一张介于满月和弦月之间的月相,而这个月相,在原本的输入中是不存在的,即生成了新的图片。