【损失函数】损失函数专题

损失函数专题

范数

L0范数

L0范数是指向量中非0的元素的个数。如果用L0规则化一个参数矩阵W，就是希望W中大部分元素是零，实现稀疏。

L0范数的应用：

特征选择：实现特征的自动选择，去除无用特征。稀疏化可以去掉这些无用特征，将特征对应的权重置为零。
可解释性（interpretability）：例如判断某种病的患病率时，最初有1000个特征，建模后参数经过稀疏化，最终只有5个特征的参数是非零的，那么就可以说影响患病率的主要就是这5个特征。

L1范数

L1范数是指向量中各个元素绝对值之和。L1范数也可以实现稀疏，通过将无用特征对应的参数W置为零实现。
L1范数：

$\|x\|_{1}=\sum_{i=1}^{N}\left|x_{i}\right| \\$

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。

L2范数

L2范数是指向量各元素的平方和然后求平方根。，用在回归模型中也称为岭回归（Ridge regression）。

L2范数：

$\|\mathbf{x}\|_{2}=\sqrt{\sum_{i=1}^{N} x_{i}^{2}} \\$

L2避免过拟合的原理是：让L2范数的规则项

$\|\mathbf{x}\|_{2} \\$

尽可能小，可以使得W每个元素都很小，接近于零，但是与L1不同的是，不会等于0；这样得到的模型抗干扰能力强，参数很小时，即使样本数据x发生很大的变化，模型预测值y的变化也会很有限。

L2范数的作用：

学习理论的角度：从学习理论的角度来说，L2范数可以防止过拟合，提升模型的泛化能力。
优化计算的角度：从优化或者数值计算的角度来说，L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。

损失函数

(一) L1损失

使用L1损失函数也被叫做最小化绝对误差(Least Abosulote Error)。这个名称非常的形象。 LAE 就是最小化真实值yi和预测值 f(xi) 之间差值 D_L1的绝对值的和。

$D_{L 1}=\sum_{i=1}^{n}\left|y_{i}-f\left(x_{i}\right)\right| \\$

这里的 D_L1其实就是平均绝对误差(MAE),使用L1 损失函数也就是min D_L1

公式：

$L 1=\sum_{i=1}^{n}\left|y_{i}-f\left(x_{i}\right)\right| \\$

导数：

$\frac{\mathrm{d} L_{1}(x)}{\mathrm{d} x}=\left\{\begin{array}{ll} 1 & \text { if } x \geq 0 \\ -1 & \text { otherwise } \end{array}\right. \\$

L1 loss 在零点不平滑，学习慢，用的较少。

1.1 平滑版L1损失 SmoothL1Loss

也被称为 Huber 损失函数。

torch.nn.SmoothL1Loss(reduction='mean')

公式：

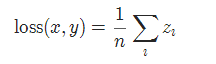
其中

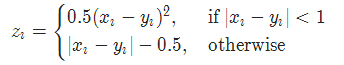
(二) L2损失

公式：

$L 2=\sum_{i=1}^{n}\left(y_{i}-f\left(x_{i}\right)\right)^{2} \\$

导数：

$\frac{\mathrm{d} L_{2}(x)}{\mathrm{d} x}=2 x \\$

L2 loss：对离群点比较敏感，如果feature 是 unbounded的话，需要好好调整学习率，防止出现梯度爆炸的情况。L2loss学习快，因为是平方增长，但是当预测值太大的时候，会在loss中占据主导位置(如真实值为1，预测多次，有一次预测值为100，其余预测为2)。

一般来说，L1正则会制造稀疏的特征，大部分无用特征的权重会被置为0。
L2正则会让特征的权重不过大，使得特征的权重比较平均。

# L1 loss
def L1_loss(y_true,y_pre):
    return np.sum(np.abs(y_true,y_pre))
# L2 loss
def L2_loss(y_true,y_pre):
    return np.sum(np.square(y_true,y_pre))

#pytorch实现
# L1 loss
# reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。
torch.nn.L1Loss(reduction='mean')

(三) 对抗损失

(四) MSE损失

不能与Smogid损失函数联用。

# reduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。
torch.nn.MSELoss(reduction='mean')

(五) 交叉熵损失

5.1 二进制交叉熵损失 BCELoss

二分类任务时的交叉熵计算函数。用于测量重构的误差, 例如自动编码机. 注意目标的值 t[i] 的范围为0到1之间。

# weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度为 “nbatch” 的 的 Tensor
torch.nn.BCELoss(weight=None, reduction='mean')

5.2 BCEWithLogitsLoss

BCEWithLogitsLoss损失函数把 Sigmoid 层集成到了 BCELoss 类中. 该版比用一个简单的 Sigmoid 层和 BCELoss 在数值上更稳定, 因为把这两个操作合并为一个层之后, 可以利用 log-sum-exp 的技巧来实现数值稳定。

# weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度 为 “nbatch” 的 Tensor
torch.nn.BCEWithLogitsLoss(weight=None, reduction='mean', pos_weight=None)

(六) 感知损失(Perceptual Loss)

感知损失的定义包含以下两个损失函数(不一定全部都要有)的，一个是feature reconstruction loss L-feat,另一个是style reconstruction loss L-style。

6.1）feature reconstruction loss L-feat 特征重建损失

如图：

现在有两幅图x和x^，把这两种图片输入到像VGG这样的预训练好的卷积网络中，最后输出了经过特征提取的 特征图，即feature maps，将这两对feature maps取一个L2损失，再除以feature maps的维度乘积。

上述的过程，就是feature reconstruction loss L-feat。L-feat是计算 loss network 中每一个特征提取层输出的L2重建损失。

6.2）style reconstruction loss L-style 风格重建损失

对于L-style, 也要先将原图输入到像VGG这样的预训练好的卷积网络，设第j层的特征图为C_jx H_j x Wj, 则通过构建一个Gram matrix G_j, 得到一个C_i x C_j 的矩阵, 矩阵的元素由下式给出:

这里G_j的数学意义是非中心协方差矩阵。每个矩阵元素为第j个特征图的c和 c' 通道上的相关性(针对同一个输入图像) . 那么L-style就是要重建目标图和生成图在各自特征通道上的相关性。

除了以上perceptual 损失外,在《Perceptual Loss for Image Translation and Style Transfer》这篇Paper中，作者还加了整体方差损失L-TV (total variation) 来保证平滑性.最终得到一个baseline的损失：

6.3）感知损失特点：

多应用于风格迁移类的任务中，这是因为预训练好的图像分类网络更加具备编码感知和语义信息的能力；
感知损失比每像素损失更可靠地度量图像相似性；感知损失不同于通常用的L1、L2重建损失在像素级别上监督图像的转化, 而是利用特征级别的重建要求来达到这一目的。
实验发现, 高层(j的值更大) 的特征重建倾向于保留图像内容和结构, 而低层(j的值更小) 的特征重建则可保留颜色, 纹理, 细节形状等。（是否说明卷积层的特性也如此？）

6.4）对Gram matrices的理解

Todo：从数学意义上理解、学习地更深入一点。

Gram matrices即非中心协方差矩阵，它的功能有：

通过矩阵乘法运算，去除了 Convolution feature 上空间结构信息。
保留代表全图的某种共性的语义信息，而这种共性恰好表现为图像的艺术风格。

(七) 循环一致损失

(八) 整体方差损失 (total variation)

(九) KL 散度损失 KLDivLoss

计算 input 和 target 之间的 KL 散度。KL 散度可用于衡量不同的连续分布之间的距离, 在连续的输出分布的空间上(离散采样)上进行直接回归时很有效。

# eduction-三个值，none: 不使用约简；mean:返回loss和的平均值；sum:返回loss的和。默认：mean。
torch.nn.KLDivLoss(reduction='mean')

(十) Focal Loss

Focal loss的公式：

\[F L\left(p_{t}\right)=-\left(1-p_{t}\right)^{\gamma} \log \left(p_{t}\right) \]

其中：

\[p_{t}=\left\{\begin{array}{lr} p & \text { if } y=1 \\ 1-p & \text { otherwise } \end{array}\right. \]

合起来就是如下形式：

\[F L=\left\{\begin{array}{rlr} -\alpha(1-p)^{\gamma} \log (p), & \text { if } & y=1 \\ -(1-\alpha) p^{\gamma} \log (1-p), & \text { if } & y=0 \end{array}\right. \]

${\gamma}$为常数，当其为0时，FL就和普通的交叉熵损失函数一致了。${\gamma}$不同取值，FL曲线如下：

目的：Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

在原有的基础上加了一个因子，其中${\gamma}>0$使得减少易分类样本的损失。使得更关注于困难的、错分的样本。

例如${\gamma}=2$，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的${\gamma}$次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

实验表明${\gamma}=2,\alpha = 0.25$ 时效果最佳。

这样以来，训练过程关注对象的排序为正难>负难>正易>负易。这就是Focal Loss，简单明了但特别有用。

代码实现：

# 实现一
def py_sigmoid_focal_loss(pred,
                          target,
                          weight=None,
                          gamma=2.0,
                          alpha=0.25,
                          reduction='mean',
                          avg_factor=None):
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
    focal_weight = (alpha * target + (1 - alpha) *
                    (1 - target)) * pt.pow(gamma)
    loss = F.binary_cross_entropy_with_logits(
        pred, target, reduction='none') * focal_weight
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

# 两个代码实现的loss是一样的，注意上下两个alpha参数。

# 实现二
class FocalLoss(nn.Module):
    def __init__(self, alpha=0.75, gamma=2, logits=False, reduce=True):
        super(FocalLoss, self).__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.logits = logits
        self.reduce = reduce

    def forward(self, inputs, targets):
        if self.logits:
            BCE_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduce=False)
        else:
            BCE_loss = F.binary_cross_entropy(inputs, targets, reduce=False)
        pt = torch.exp(-BCE_loss)
        F_loss = self.alpha * (1-pt)**self.gamma * BCE_loss

        if self.reduce:
            return torch.mean(F_loss)
        else:
            return F_loss

其中focal_weight代表的是如下公式：

\[\text { FocalWeight }=\left\{\begin{array}{lll} \alpha(1-p)^{\gamma}, & \text { if } & \text { target }=1 \\ (1-\alpha) p^{\gamma}, & \text { if } & \text { target }=0 \end{array}\right. \]

激活函数

Sigmoid函数

sigmoid常用于二元分类，将二元输入映射成0和1。

函数：

$f(z)=\frac{1}{1+e^{-z}} \\$

导数：

$\mathrm{f}^{\prime}(\mathrm{z})=\mathrm{f}(\mathrm{z})(1-\mathrm{f}(\mathrm{z})) \\$

sigmoid函数推导：

$\begin{aligned} f^{\prime}(z) &=\left(\frac{1}{1+e^{-z}}\right)^{\prime} \\ &=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1+e^{-z}-1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{\left(1+e^{-z}\right)}\left(1-\frac{1}{\left(1+e^{-z}\right)}\right) \\ &=f(z)(1-f(z)) \end{aligned} \\$

其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。sigmoid函数把一个值映射到0-1之间。

该函数具有如下的特性：当x趋近于负无穷时，y趋近于0；当x趋近于正无穷时，y趋近于1；当x= 0时，y=0.5.

优点：

Sigmoid函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。
求导容易，处处可导，导数为：f′(x)=f(x)(1−f(x))

缺点：

由于其软饱和性，容易产生梯度消失，导致训练出现问题。
其输出并不是以0为中心的。
当激活函数使用Sigmoid时，损失函数不建议使用均方误差，而用交叉熵损失函数代替。Sigmoid()函数和均方误差联用可能会导致梯度消失的问题。

BN理解

Batch Normalization批标准化

机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。那BatchNorm的作用是什么呢？BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。

BN的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

具体实现：

BN在训练的时候可以根据Mini-Batch里的若干训练实例进行激活数值调整，但是在推理（inference）的过程中，从所有训练实例中获得的统计量来代替Mini-Batch里面m个训练实例获得的均值和方差统计量。

BatchNorm为什么NB呢？关键还是效果好。经过简单的变换，带来的好处多得很，这也是为何现在BN这么快流行起来的原因。