【数据结构】并查集学习

【数据结构】并查集

1. 并查集的定义

并查集是一种维护集合的数据结构，它的名字中“并”“查”“集”分别取自Union（合并）、Find（查找）、Set（集合）这3个单词。也就是说，并查集支持下面两个操作：

① 合并：合并两个集合。

② 查找：判断两个元素是否在一个集合。

那么并查集是用什么实现的呢？其实就是用一个数组：

int father[N];

其中father[i]表示元素 i 的父亲结点，而父亲结点本身也是这个集合内的元素（1≤i≤N）。例如father[1]=2就表示元素1的父亲结点是元素2，以这种父系关系来表示元素所属的集合。另外，如果father[i]=i，则说明元素 i 是该集合的根结点，但对同一个集合来说只存在一个根结点，且将其作为所属集合的标识。

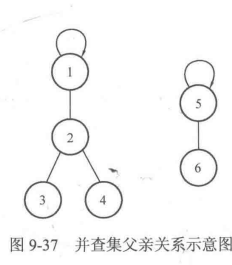
举个例子，下面给出了图9-37的father数组情况。

    father[1]=1; //1的父亲结点是自己，也就是说1号是根结点
    father[2]=1; //2的父亲结点是1
    father[3]=2; //3的父亲结点是2
    father[4]=2; //4的父亲结点是2
    father[5]=5; //5的父亲结点是自己，也就是说5号是根结点
    father[6]=5; //6的父亲结点是5

在图9-37中，father[1]=1说明元素1的父亲结点是自己，即元素1是集合的根结点。
father[2]=1说明元素2的父亲结点是元素1，father[3]=2和father[4]=2说明元素3和元素4的父亲结点都是元素2，这样元素1、2、3、4就在同一个集合当中。father[5]=5和father[6] =5则说明5和6是以5为根结点的集合。这样就得到了两个不同的集合。

2. 并查集的基本操作

总体来说，并查集的使用需要先初始化father数组，然后再根据需要进行查找或合并的操作。

1. 初始化

一开始，每个元素都是独立的一个集合，因此需要令所有father[i]等于i：

for(int i=1;i<=N;i++){
	father[i]=i;	//令fatherti]为-1也可，此处以father[i]=i为例
}

2. 查找

由于规定同一个集合中只存在一个根结点，因此查找操作就是对给定的结点寻找其根结点的过程。实现的方式可以是递推或是递归，但是其思路都是一样的，即反复寻找父亲结点，直到找到根结点（即father[i]=i的结点）。
先来看递推的代码：

int findFather(int x){
    while(x!=father[x])
        x=father[x];
    return x;
}

当然，这个过程也可以用递归来实现：

int findFather(int x){
    if(x==father[x]) 
        return x;
    else
        return findFather(father[x]);
}

3. 合并

合并是指把两个集合合并成一个集合，题目中一般给出两个元素，要求把这两个元素所在的集合合并。具体实现上一般是先判断两个元素是否属于同一个集合，只有当两个元素属于不同集合时才合并，而合并的过程一般是把其中一个集合的根结点的父亲指向另一个集合的根结点。
于是思路就比较清晰了，主要分为以下两步：

1. 对于给定的两个元素a、b，判断它们是否属于同一集合。可以调用上面的查找函数，对这两个元素a、b分别查找根结点，然后再判断其根结点是否相同。

2. 合并两个集合：在①中已经获得了两个元素的根结点faA与faB，因此只需要把其中一个的父亲结点指向另一个结点。例如可以令father[faA]=faB，当然反过来令father[faB]= faA也是可以的，两者没有区别。
   还是以图9-34为例，把元素4和元素6合并，过程如下：

   • 判断元素4和元素6是否属于同一个集合：元素4所在集合的根结点是1，元素6所在集合的根结点是5，因此它们不属于同一个集合。
   • 合并两个集合：令father[5]=1，即把元素5的父亲设为元素1。
     现在可以写出合并的代码了：

   void Union(int a,int b){
       int faA=findFather(a);
       int faB=findFather(b);
       if(faA!=faB)
           father[faA] = faB;
   }
   

   最后说明并查集的一个性质。在合并的过程中，只对两个不同的集合进行合并，如果两个元素在相同的集合中，那么就不会对它们进行操作。这就保证了在同一个集合中一定不会产生环，即并查集产生的每一个集合都是一棵树。

3. 路径压缩

上面讲解的并查集查找函数是没有经过优化的，在极端情况下效率较低。现在来考虑一种情况，即题目给出的元素数量很多并且形成一条链，那么这个查找函数的效率就会非常低。
如图9-40所示，总共有105个元素形成一条链，那么假设要进行105次查询，且每次查询都查询最后面的结点的根结点，那么每次都要花费105的计算量查找，这显然无法承受。

那应该如何去优化查询操作呢？
由于findFather函数的目的就是查找根结点，例如下面这个例子：

father[1]=1;
father[2]=1;
father[3]=2;
father[4]=3;

因此，如果只是为了查找根结点，那么完全可以想办法把操作等价地变成：

father[1]=1;
father[2]=1;
father[3]=1;
father[4]=1;

对应图形的变化过程如图9-41所示：

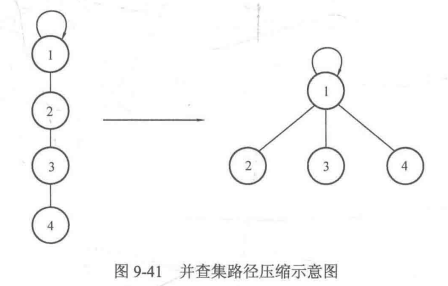
这样相当于把当前查询结点的路径上的所有结点的父亲都指向根结点，查找的时候就不需要一直回溯去找父亲了，查询的复杂度可以降为O(1)。
那么，如何实现这种转换呢？回忆之前查找函数findFather()的查找过程，可以知道是从给定结点不断获得其父亲结点而最终到达根结点的。
因此转换的过程可以概括为如下两个步骤：

1. 按原先的写法获得x的根结点r。

2. 重新从x开始走一遍寻找根结点的过程，把路径上经过的所有结点的父亲全部改为根结点r。

   于是可以写出代码：

int findFather(int x){
    int a=x;//由于x在while循环时会变成根结点，因此先把原先的x保存一下
    while(x!=father[x])
        x = father[x];
    
    //到这里，x存放的就是根结点
    while(a!=father[a]){
        int z = a;//因为a要被father[a]覆盖，所以先保存a的值，以便修改father[a]
        a = father[a];
        father[z] = x;//将原先的结点a的父亲改为根结点x
    }
   return x; //返回根结点
}

这样就可以在查找时把寻找根结点的路径压缩了。
由于涉及一些复杂的数学推导，读者可以把路径压缩后的并查集查找函数均摊效率认为是一个几乎为O（1）的操作。而喜欢递归的读者，也可以采用下面的递归写法：

int findFather(int v){
    if(v==father[v])
        return v;
    else{
        int F=findFather(father[v]); //递归找到根结点并赋给F
        father[v] = F;
        return F;//返回根结点F
    }
}

4. 并查集题目

1. 已知不相交集合用数组表示为{4,6,5,2，-3，-4,3}。若集合元素从1到7编号，则调用Union(Find(7),Find(1))(按规模求并并且带路径压缩后的结果数组为

   [ ]   A.{ 4, 6, 5, 2, 6, -7, 3 }
   [ ]   B.{ 4, 6, 5, 2, -7, 5, 3 }
   [ ]   C.{ 6, 6, 5, 6, -7, 5, 5 }
   [√]  D.{ 6, 6, 5, 6, 6, -7, 5 }

   /*解析：按大小合并，所以集合{5,3,7}并入集合{6,2,4,1}，
6是根结点，树根大小为-7，又因为包含路径压缩，
所以6成为原始集合元素2，4，1的直接父亲，
并成为新假入集合根5的直接父亲，5也成为3和7的直接父亲。*/

2. 在并查集问题中，已知集合元素0~8所有对应的父结点编号值分别是{ 1, -4, 1, 1, -3, 4, 4, 8, -2 }（注：−n表示树根且对应集合大小为n），那么将元素6和8所在的集合合并（要求必须将小集合并到大集合）后，该集合对应的树根和父结点编号值分别是多少？

   [ ]   A.1和-6
   [√]  B.4和-5
   [ ]   C.8和-5
   [ ]   D.8和-6

   /*解析：6和8合并就是集合{4,5,6}、{7,8}合并，大并小，
所以{7,8}并入{4,5,6}，根结点是4，计数为-5。*/