【算法理论】动归入门[C语言描述]
动归入门 [C语言描述]
源自《算法笔记》
1 动归简介
动态规划是一种用来解决一类最优化问题的算法思想。动态规划在一个复杂的问题分解成若干个子问题。通过综合此问题的最优解。来得到原问题的最优解。
需要注意的是，会将每个求解过的子问题的解记录下来。这样当下一次再碰到同样的子问题时，不可以直接使用之前记录的结果而不是重复计算。
一般可以使用递归或者递推的写法来实现动态规划。其中递归写法在此处又称为记忆化搜索。
2 动归的递归写法
以菲波那切数列为例。
#include<stdio.h>
int dp[100];
/* 斐波那契的动态规划实现 */
int Fbi(int n){
if(n==0 || n==1)
{
dp[n] = 1;
return dp[n];
}
if(dp[n] != -1)
{
return dp[n]; //直接返回结果,直接返回结果不再重复计算。
}
else
{
dp[n] = Fbi(n-1) + Fbi(n-2); //计算结果并保存在dp[n]中
return dp[n];
}
}
int main()
{
for(int i = 0; i< 100; i++)
{
dp[i] = -1;
}
Fbi(41);
for(int i = 0; i< 40; i++)
{
printf("%d ", dp[i]);
}
return 0;
}
这样就把已经计算过的内容记录了下来，于是当下次再碰到需要计算相同的内容时，就能直接使用上次计算的结果，这可以省去大半无效计算，而这也是记忆化搜索这个名字的由来。
通过上面的例子可以引申出一个概念：如果一个问题可以被分解为若干个子问题，且这些子问题会重复出现，那么就称这个问题拥有重叠子问题。动态规划通过记录重叠子问题的解，来使下次碰到相同的子问题时直接使用之前记录的结果，以此避免大量重复计算。因此，一个问题必须拥有重叠子问题，才能使用动态规划去解决。
3 动归的递推写法
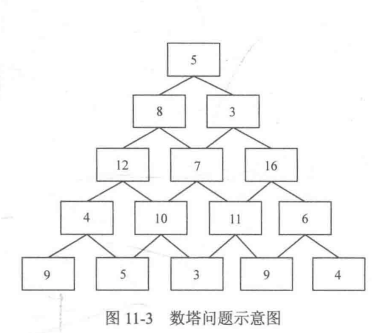
以经典的数塔问题为例，如图11-3所示，将一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字……第n层有n个数字。现在要从第一层走到第n层，每次只能走向下一层连接的两个数字中的一个，问：最后将路径上所有数字相加后得到的和最大是多少？
一开始，从第一层的5出发，按5→8→7的路线来到7，并枚举从7出发的到达最底层的所有路径。但是，之后当按5→3→7的路线再次来到7时，又会去枚举从7出发的到达最底层的所有路径，这就导致了从7出发的到达最底层的所有路径都被反复地访问，做了许多多余的计算。事实上，可以在第一次枚举从7出发的到达最底层的所有路径时就把路径上能产生的最大和记录下来，这样当再次访问到7这个数字时就可以直接获取这个最大值，避免重复计算。
由上面的考虑不妨令dp[i][j]表示从第 i 行第 j 个数字出发的到达最底层的所有路径中能得到的最大和，例如dp[3][2]就是图中的 7 到最底层的路径最大和。在定义这个数组之后，dp[1][1]就是最终想要的答案，现在想办法求出它。
注意到一个细节：如果要求出“从位置（1，1）到达最底层的最大和”dp[1][1]，那么一定要先求出它的两个子问题“从位置（2，1）到达最底层的最大和dp[2][1]”和“从位置（2，2）到达最底层的最大和dp[2][2]”，即进行了一次决策：走数字5的左下还是右下。于是dp[l][1]就是dp[2][1]和dp[2][2]的较大值加上5。写成式子就是：
dp[1][1]=max(dp[2][1],dp[2][2])+f[1][1]
由此可以归纳得到这么一个信息：如果要求出dp[i][i]，那么一定要先求出它的两个子问题“从位置（i+1，j）到达最底层的最大和dp[i+1][j]”和“从位置（i+1，j+1）到达最底层的最大和dp[i+1][j+1]”，即进行了一次决策：走位置（i，j）的左下还是右下。于是dp[i][i]就是dp[i+1][i]和dp[i+1][i+1]的较大值加上f[i][j]。写成式子就是：
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j]
把dp[i][j]称为问题的状态，而把上面的式子称作状态转移方程，它把状态dp[i][j]转移为dp[i+1][j]和dp[i+1][i+1]。可以发现，状态dp[i][j]只与第 i+1 层的状态有关，而与其他层的状态无关，这样层号为i的状态就总是可以由层号为 i+1 的两个子状态得到。那么，如果总是将层号增大，什么时候会到头呢？可以发现，数塔的最后一层的dp值总是等于元素本身，即dp[n][i]=f[n][j] (1≤j≤n），把这种可以直接确定其结果的部分称为边界，而动态规划的递推写法总是从这些边界出发，通过状态转移方程扩散到整个dp数组。
这样就可以从最底层各位置的dp值开始，不断往上求出每一层各位置的dp值，最后就会得到dp[1][1]，即为想要的答案。
这种思想的动态规划代码如下：
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
scanf("%d",&f[i][j]);
//边界
for(int j=1;j<=n;j++)
dp[n][j] = f[n][j];
//从第n-1层不断往上计算出dp[i][j]
for(int i=n-1;i>=1;i--)
for(int j=i;j<=i;j++){
dp[i][j] = max(dp[i+1][j],dp[i+1][j+1])+f[i][j];//状态转移方程
}
printf("%d\n",dp[1][1]);//dp[1][1]即为需要的答案‘’
return 0;
}
-
递推写法和递归写法的区别：
显然，使用递归也可以实现上面的例子（即从
dp[1][1]开始递归，直至到达边界时返回结果）。两者的区别在于：使用递推写法的计算方式是自底向上（Bottom-up Approach），即从边界开始，不断向上解决问题，直到解决了目标问题；而使用递归写法的计算方式是自顶向下（Top-down Approach），即从目标问题开始，将它分解成子问题的组合，直到分解至边界为止。
通过上面的例子再引申出一个概念：如果一个问题的最优解可以由其子问题的最优解有效地构造出来，那么称这个问题拥有最优子结构（Optimal Substructure）。最优子结构保证了动态规划中原问题的最优解可以由子问题的最优解推导而来。因此，一个问题必须拥有最优子结构，才能使用动态规划去解决。例如数塔问题中，每一个位置的dp值都可以由它的两个子问题推导得到。
至此，重叠子问题和最优子结构的内容已介绍完毕。需要指出，一个问题必须拥有重叠子问题和最优子结构，才能使用动态规划去解决。下面指出这两个概念的区别：
- 分治与动态规划。分治和动态规划都是将问题分解为子问题，然后合并子问题的解得到原问题的解。但是不同的是，分治法分解出的子问题是不重叠的，因此分治法解决的问题不拥有重叠子问题，而动态规划解决的问题拥有重叠子问题。例如，归并排序和快速排序都是分别处理左序列和右序列，然后将左右序列的结果合并，过程中不出现重叠子问题，因此它们使用的都是分治法。另外，分治法解决的问题不一定是最优化问题，而动态规划解决的问题一定是最优化问题。
- 贪心与动态规划。贪心和动态规划都要求原问题必须拥有最优子结构。二者的区别在于，贪心法采用的计算方式类似于上面介绍的“自顶向下”，但是并不等待子问题求解完毕后再选择使用哪一个，而是通过一种策略直接选择一个子问题去求解，没被选择的子问题就不去求解了，直接抛弃。也就是说，它总是只在上一步选择的基础上继续选择，因此整个过程以一种单链的流水方式进行，显然这种所谓“最优选择”的正确性需要用归纳法证明。例如对数塔问题而言，贪心法从最上层开始，每次选择左下和右下两个数字中较大的一个，一直到最底层得到最后结果，显然这不一定可以得到最优解。而动态规划不管是采用自底向上还是自顶向下的计算方式，都是从边界开始向上得到目标问题的解。也就是说，它总是会考虑所有子问题，并选择继承能得到最优结果的那个，对暂时没被继承的子问题，由于重叠子问题的存在，后期可能会再次考虑它们，因此还有机会成为全局最优的一部分，不需要放弃。所以贪心是一种壮士断腕的决策，只要进行了选择，就不后悔；动态规划则要看哪个选择笑到了最后，暂时的领先说明不了什么。
