词法分析器1(正则表达式到ε-NFA的转换)
自动机
关于自动机的说明，这里不不再复述，请到http://zh.wikipedia.org/wiki/自动机查看。
表达式
首先，我们规定表达式中只允许输入Char_Type和String_Type类型的字符。
template <typename Char_Type, typename String_Type> class Rule { };
ε-NFA的状态
对于一个状态来说，我们并不需要知道他的任何信息
在上面的代码中，为了调试方便，我为其加入了idx域，并为每个状态分配了一个唯一的ID。
struct EpsilonNFA_State { #ifdef _DEBUG uint idx; EpsilonNFA_State() { idx = inc(); } static uint inc() { static uint i = 0; return i++; } #else EpsilonNFA_State() {} #endif };
ε-NFA的边
ε-NFA中的边都是有向的。对于任意一条边来说，最重要的是他的两个端点是谁以及这条边所对应的字符集（若这条边不是ε边）。
struct EpsilonNFA_Edge { struct { Char_Type char_value; String_Type string_value; }data; enum Edge_Type { TUnknown = 0, TNot = 1, TChar = 2, TString = 4, TEpsilon = 8 }; uchar edge_type; EpsilonNFA_State* pFrom; EpsilonNFA_State* pTo; EpsilonNFA_Edge(EpsilonNFA_State* pFrom, EpsilonNFA_State* pTo) : edge_type(TEpsilon), pFrom(pFrom), pTo(pTo) {} EpsilonNFA_Edge(const Char_Type& x, EpsilonNFA_State* pFrom, EpsilonNFA_State* pTo) : edge_type(TChar), pFrom(pFrom), pTo(pTo) { data.char_value = x; } EpsilonNFA_Edge(const String_Type& x, EpsilonNFA_State* pFrom, EpsilonNFA_State* pTo) : edge_type(TString), pFrom(pFrom), pTo(pTo) { data.string_value = x; } inline void negate() { edge_type ^= TNot; } inline const bool isNot()const { return (edge_type & TNot) == TNot; } inline const bool isEpsilon()const { return (edge_type & TEpsilon) == TEpsilon; } inline const bool isChar()const { return (edge_type & TChar) == TChar; } inline const bool isString()const { return (edge_type & TString) == TString; } const Edge_Type edgeType()const { if (isEpsilon()) return TEpsilon; else if (isChar()) return TChar; else if (isString()) return TString; else return TUnknown; } };
有了以上两个结构之后，我们为Rule添加三个成员变量
EpsilonNFA_State *pEpsilonStart, *pEpsilonEnd;
hashmap<EpsilonNFA_State*, vector<EpsilonNFA_Edge>, _hash> epsilonNFA_Edges;
pEpsilonStart和pEpsilonEnd分别表示这条表达式所对应状态机的start和end状态，epsilonNFA_Edges则是以某个状态作为key，从这个状态到达另一个状态所经过的边作为value的hash表。
生成状态机
终于到了正题，首先，我们把所有的关系分为串联关系、并联关系、可选关系、0次及以上的重复关系、至少1次以上的重复关系和取反关系。下面分别介绍每种关系的ε-NFA如何来生成。（下文中若没有指出连接边的类型则是ε边）
字符集
正如上文所说，字符集包括Char_Type和String_Type类型的字符，应此生成字符集的状态机就比较简单了，只需创建出两个状态，然后通过一条经过这个字符集的边将这两个状态按照某个方向连接，最后将一个状态标记为start状态，另一个状态标记为end状态即可。
Rule(const Char_Type& x, Context& context) : pDFAStart(NULL), context(context) { pEpsilonStart = EpsilonNFA_State_Alloc::allocate(); construct(pEpsilonStart); pEpsilonEnd = EpsilonNFA_State_Alloc::allocate(); construct(pEpsilonEnd); epsilonNFA_Edges[pEpsilonStart].push_back(EpsilonNFA_Edge(x, pEpsilonStart, pEpsilonEnd)); context.epsilonNFA_States.insert(pEpsilonStart); context.epsilonNFA_States.insert(pEpsilonEnd); } Rule(const String_Type& x, Context& context) : pDFAStart(NULL), context(context) { pEpsilonStart = EpsilonNFA_State_Alloc::allocate(); construct(pEpsilonStart); pEpsilonEnd = EpsilonNFA_State_Alloc::allocate(); construct(pEpsilonEnd); epsilonNFA_Edges[pEpsilonStart].push_back(EpsilonNFA_Edge(x, pEpsilonStart, pEpsilonEnd)); context.epsilonNFA_States.insert(pEpsilonStart); context.epsilonNFA_States.insert(pEpsilonEnd); }
串联关系
串联关系中，只需要将前一个状态机的end状态通过ε边连接到另一个状态机的start状态，最后将前一个状态的start状态标记为新状态机的start状态，后一个状态机的end状态标记为新状态机的end状态即可。
self operator+(const self& x) { self a = cloneEpsilonNFA(*this), b = cloneEpsilonNFA(x); copyEpsilonNFA_Edges(b, a); a.epsilonNFA_Edges[a.pEpsilonEnd].push_back(EpsilonNFA_Edge(a.pEpsilonEnd, b.pEpsilonStart)); a.pEpsilonEnd = b.pEpsilonEnd; return a; }
并联关系
并联关系中，需要分别新建一个start和end状态做为新状态机的start和end状态，然后将新生成的start状态分别连接到原状态机的start状态，原状态机的end状态连接到新生成的end状态即可。
self operator|(const self& x) { self a = cloneEpsilonNFA(*this), b = cloneEpsilonNFA(x); copyEpsilonNFA_Edges(b, a); EpsilonNFA_State* _pStart = EpsilonNFA_State_Alloc::allocate(); construct(_pStart); EpsilonNFA_State* _pEnd = EpsilonNFA_State_Alloc::allocate(); construct(_pEnd); context.epsilonNFA_States.insert(_pStart); context.epsilonNFA_States.insert(_pEnd); a.epsilonNFA_Edges[_pStart].push_back(EpsilonNFA_Edge(_pStart, a.pEpsilonStart)); a.epsilonNFA_Edges[_pStart].push_back(EpsilonNFA_Edge(_pStart, b.pEpsilonStart)); a.epsilonNFA_Edges[a.pEpsilonEnd].push_back(EpsilonNFA_Edge(a.pEpsilonEnd, _pEnd)); a.epsilonNFA_Edges[b.pEpsilonEnd].push_back(EpsilonNFA_Edge(b.pEpsilonEnd, _pEnd)); a.pEpsilonStart = _pStart; a.pEpsilonEnd = _pEnd; return a; }
重复关系
在正则表达式中存在形如(a)+和(a)*的两种重复关系，对于这两种重复关系，生成的状态机的区别仅在于end状态对于一次以上的重复，只需要给原状态机添加一条从end状态到start状态的ε边即可。而对于零次以上的重复，不光需要添加ε边，同时需要将新状态机的end状态标记为start状态，因为零次重复时不需要经过任意边既可被接受。
self operator*() { self a = cloneEpsilonNFA(*this); a.epsilonNFA_Edges.insert(EpsilonNFA_Edge(a.pEpsilonEnd, a.pEpsilonStart)); a.pEpsilonEnd = a.pEpsilonStart; return a; } self operator+() { self a = cloneEpsilonNFA(*this); a.epsilonNFA_Edges[a.pEpsilonEnd].push_back(EpsilonNFA_Edge(a.pEpsilonEnd, a.pEpsilonStart)); return a; }
上面这三种是最基本的生成方法，通过以上这三种生成方法已足够应付多数的表达式。
一些拓展
下面来看看一些拓展形式的状态机是如何生成的。
可选关系
在可选关系中，只需要给原状态机添加一条从start状态到end状态的ε边即可。由于ε-NFA只允许有一个start和end状态的关系，应此当条件不成立时从start状态就可直接通过ε边到达end状态。
inline self opt() { self a = cloneEpsilonNFA(*this); a.epsilonNFA_Edges[a.pEpsilonStart].push_back(EpsilonNFA_Edge(a.pEpsilonStart, a.pEpsilonEnd)); return a; }
取反关系
由于我们只处理Char_Type和String_Type类型的字符集，应此对于取反我们只需要将当前状态机内所有类型为TChar或TString类型的边取一下反即可（需要注意的是可能存在负负得正的情况，既取偶数次反等于没取反）
self operator!() { self a = cloneEpsilonNFA(*this); for (typename hashmap<EpsilonNFA_State*, vector<EpsilonNFA_Edge>, _hash>::iterator i = a.epsilonNFA_Edges.begin(), m = a.epsilonNFA_Edges.end(); i != m; ++i) { for (typename vector<EpsilonNFA_Edge>::iterator j = i->second.begin(), n = i->second.end(); j != n; ++j) { if (j->isChar() || j->isString()) j->negate(); } } return a; }
Char-Char关系
所谓的char-char关系就是正则表达式中的[a-z]表达式。其实这是一种并联关系的拓展，由两个原始状态机拓展到了N个，生成方法也类似。
self operator-(const self& x) { self a = cloneEpsilonNFA(*this); if (epsilonNFA_Edges.size() == 1 && x.epsilonNFA_Edges.size() == 1 && epsilonNFA_Edges.begin()->second.size() == 1 && x.epsilonNFA_Edges.begin()->second.size() == 1 && epsilonNFA_Edges.begin()->second.begin()->edge_type == EpsilonNFA_Edge::TChar && x.epsilonNFA_Edges.begin()->second.begin()->edge_type == EpsilonNFA_Edge::TChar) { EpsilonNFA_State* _pStart = EpsilonNFA_State_Alloc::allocate(); construct(_pStart); EpsilonNFA_State* _pEnd = EpsilonNFA_State_Alloc::allocate(); construct(_pEnd); context.epsilonNFA_States.insert(_pStart); context.epsilonNFA_States.insert(_pEnd); a.epsilonNFA_Edges[_pStart].push_back(EpsilonNFA_Edge(_pStart, a.pEpsilonStart)); a.epsilonNFA_Edges[a.pEpsilonEnd].push_back(EpsilonNFA_Edge(a.pEpsilonEnd, _pEnd)); const Char_Type chStart = epsilonNFA_Edges.begin()->second.begin()->data.char_value; const Char_Type chEnd = x.epsilonNFA_Edges.begin()->second.begin()->data.char_value; for (Char_Type ch = chStart + 1; ch < chEnd; ++ch) { self y(ch, context); copyEpsilonNFA_Edges(y, a); a.epsilonNFA_Edges[_pStart].push_back(EpsilonNFA_Edge(_pStart, y.pEpsilonStart)); a.epsilonNFA_Edges[y.pEpsilonEnd].push_back(EpsilonNFA_Edge(y.pEpsilonEnd, _pEnd)); } self b = cloneEpsilonNFA(x); copyEpsilonNFA_Edges(b, a); a.epsilonNFA_Edges[_pStart].push_back(EpsilonNFA_Edge(_pStart, b.pEpsilonStart)); a.epsilonNFA_Edges[b.pEpsilonEnd].push_back(EpsilonNFA_Edge(b.pEpsilonEnd, _pEnd)); a.pEpsilonStart = _pStart; a.pEpsilonEnd = _pEnd; } else { throw error<string>("doesn't support", __FILE__, __LINE__); } return a; }
尾声
让我们来编写一个函数来打印出整个生成后的状态机。
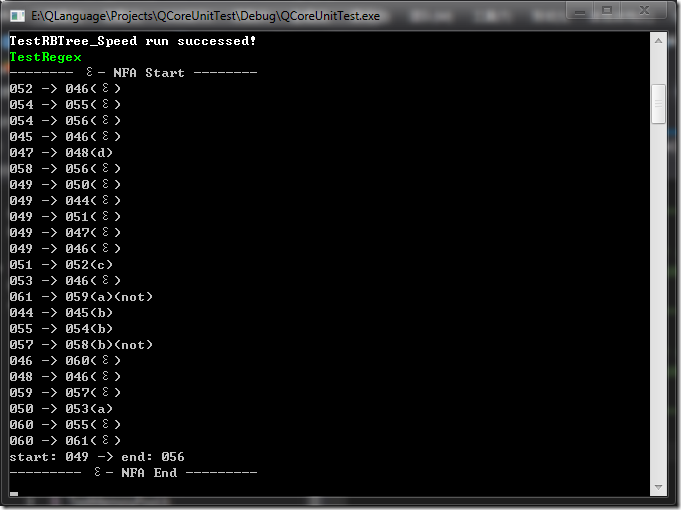
void printEpsilonNFA() { printf("-------- ε- NFA Start --------\n"); for (typename hashmap<EpsilonNFA_State*, vector<EpsilonNFA_Edge>, _hash>::const_iterator i = epsilonNFA_Edges.begin(), m = epsilonNFA_Edges.end(); i != m; ++i) { for (typename vector<EpsilonNFA_Edge>::const_iterator j = i->second.begin(), n = i->second.end(); j != n; ++j) { printf("%03d -> %03d", j->pFrom->idx, j->pTo->idx); switch (j->edgeType()) { case EpsilonNFA_Edge::TEpsilon: printf("(ε)"); break; case EpsilonNFA_Edge::TChar: printf("(%c)", j->data.char_value); break; case EpsilonNFA_Edge::TString: printf("(%s)", j->data.string_value.c_str()); break; default: break; } if (j->isNot()) printf("(not)"); printf("\n"); } } printf("start: %03d -> end: %03d\n", pEpsilonStart->idx, pEpsilonEnd->idx); printf("--------- ε- NFA End ---------\n"); }
最后我们来编写一些测试代码来试试生成效果如何
Rule_Type::Context context; Rule_Type a('a', context), b('b', context), d('d', context); Rule_Type result = (a - d).opt() + (+b | !(a + b)); #ifdef _DEBUG result.printEpsilonNFA(); #endif
可打印出如下内容
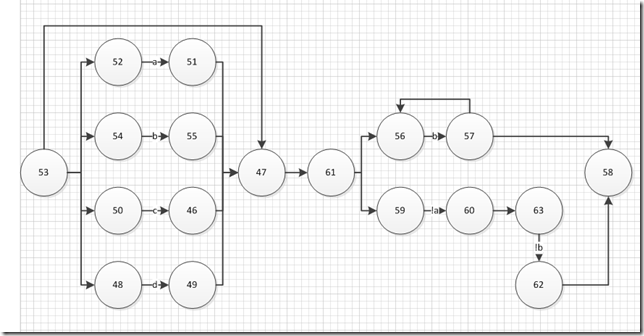
最后形成形如下图的状态机
完整的代码可到http://code.google.com/p/qlanguage下载。
