进制转换详解，二进制，十进制，八进制，十六进制，62进制，MD5加密，python代码示例

进制转换详解，二进制，十进制，八进制，十六进制，62进制，MD5加密，python代码示例

进制关系讲解：

1. 进制的产生：

首先说一下十进制，这是我们最熟悉的进制体系，理论上也是我们人类最先接触的进制体系。
原因很简单，我们人都有十个手指头和十个脚指头。这天然的对称性，有着天然的数学规律在里面。
十进制是应用最广泛，也最常用的进制体系，但是进制体系并不只属于十进制。
第二个被发现，并广泛使用的是二进制，大概有和无，也是最先被明白的道理吧。
从二进制开始人类才算真正打开进制世界的大门，并且一发不可收拾。
比如：太极阴阳，八卦，摩尔斯密码，八进制，十六进制等等。

2. 进制原理：

进制实际上是一种数的认知和规律总结。
进制转换实际上就是一种数与数之间的对应关系。（这一点和加密原理一样）
既然是一种对应关系，那么一定存在某种我们人类认知的数学规则在里面。
最基础的知识就是符号，进位和减位。
比如：15-7=8
实质上就是5-7=-2+10=8：这个过程可以理解为5减7，不够向10借2，5+2=7,7-7=0
最后 10-2=8，这样 10 借出 2 之后还剩 8，15-7=8.
在减法的基础上，发展出除法，余数和商。除法，余数，商，这三个就是进位换算的数学基础。

3. 十进制举例：

首先人为定义一个数字范围（符号）为：0,1,2,3,4,5,6,7,8,9
再定义一个进位规则：逢十进一
再定义一个显示的规则：向左进位
    举例说明：9+1=10
    9 已经是数字范围的最大值，再加 1，只能向上进位，个位数变成 0，十位数变成 1
	组合起来按照向左进位显示就是 10
    实际我们可以理解为每一个数的左边都有无数的 0 位存在
如：0010，按照十进制理解是十, 10 前面的 0 被我们省略掉了而已。每一位可以显示 0~9 的值
当位值达到9还要继续增加的时候，实际上就是向上进位，自身归 0，加法就是重复这个过程的规则
最后得到一个固定的组合值，显示成一个数字，减法反之。
    能理解上面这段话，就基本上理解了进制规则和方法。
    举例：100，按照十进制，解读为：百位值：1，十位值：0，个位值：0
    100+100=200 的过程：百位值 1+1，十位 +0，个位 +0，最后显示为：200

python代码示例：

十进制转二进制：

# 二进制：
# 1. 数字范围：0,1
# 2. 进位规则：逢二进一
# 3. 显示规则：向左进位

NUM = ["0", "1"]	# 数字范围：0,1

def z2(func_num):	# 定义一个函数
    len_count = len(NUM)	# 得到进位规则的值
    result_value = []	# 定义一个空的列表用来放得到的新数据
    while func_num >= len_count:	# 循环比较当前的商是不是大于等于进位规则的值
        func_num,remain = divmod(func_num,len_count)	# 得到给定十进制数的商和余数
        result_value.append(NUM[remain])		# 把余数对应的数字范围值按顺序放进列表
    result_value.append(NUM[func_num])		# 把最后剩余的商对应的数字范围值放进列表
    result_value.reverse()		# 反转列表

    result = "".join(result_value)		# 把列表里的字符串拼接起来
    return result

test = z2(10)
print(test)

十进制转八进制：

# 八进制：
# 1. 数字范围：0~7
# 2. 进位规则：逢八进一
# 3. 显示规则：向左进位

NUM = ["0", "1", "2", "3", "4", "5", "6", "7"]

def z8(func_num):
    len_count = len(NUM)
    result_value = []
    while func_num >= len_count:
        func_num, remain = divmod(func_num, len_count)
        result_value.append(NUM[remain])
    result_value.append(NUM[func_num])
    result_value.reverse()

    result = "".join(result_value)
    return result

test = z8(10)
print(test)

十进制转十六进制：

# 十六进制：
# 1. 数字范围：0~F
# 2. 进位规则：逢十六进一
# 3. 显示规则：向左进位

NUM = ["0", "1", "2", "3", "4", "5", "6", "7","8","9","A","B","C","D","E","F"]

def z16(func_num):
    len_count = len(NUM)
    result_value = []
    while func_num >= len_count:
        func_num, remain = divmod(func_num, len_count)
        result_value.append(NUM[remain])
    result_value.append(NUM[func_num])
    result_value.reverse()

    result = "".join(result_value)
    return result

test = z16(10)
print(test)

十进制转62进制：

# 62进制：
# 1. 数字范围：0~9A~Za~z
# 2. 进位规则：逢62进一
# 3. 显示规则：向左进位

import string
import itertools
# 实在是不想写这个长列表了，string和itertools 模块，其实也就是把这些字符变成字符串，放进列表
NUM = list(itertools.chain(string.digits, string.ascii_uppercase, string.ascii_lowercase))

def z62(func_num):
    len_count = len(NUM)
    result_value = []
    while func_num >= len_count:
        func_num, remain = divmod(func_num, len_count)
        result_value.append(NUM[remain])
    result_value.append(NUM[func_num])
    result_value.reverse()

    result = "".join(result_value)
    return result

test = z62(10)
print(test)

结语：

​ 可以看出，这些进制的本质都只是更换了数字范围和进位规则
​ 于是通过十进制作为中间值，他们之间可以实现互相转换。
​ 因为我们规定的向左进位的规则，导致左边的位值大于右边的位值
​ 所以实际的排列顺序和除法所得余数的顺序刚好相反：
​ 商>倒数第一个余数>倒数第二个余数>......>第一个余数。

为什么最后排序要反转顺序呢？
因为这就涉及到加权的概念，什么是加权呢？
举例：十进制 90 > 9
其实 9 和 9 值是一样的，为什么 90 就大于 9 呢？
因为 90 = 9 * 10  这个 10 就是权重
表明 9 现在代表的是十位上的 9 也就是 10 个 9 的意思
所以 10 个 9 自然大于 1 个 9

以整数 125 为例，转换为二进制数：
我们规定的进位规则是：向左进位，这就导致了 左边值>右边值 [ 10 > 01 ]
下面我们看看二进制加权如何表示：

	125 的二进制表示就是：1111101
以上示例可以说明，二进制是如何加权的：左边的权值 = 右边权值 * 进位规则
先比较大小，再得到和位值的差，可以得到加权值和位值
但是减法效率太差，而且涉及到比对判断

一般都是使用 除 2 取余法：
有商或者余数就代表该位权值位存在，余数值就是该位的具体值
权重来自于商的层数，而商的层数实际上是底层权值最高
为什么权重来自于商呢？
因为 125 按照进位规则除下去，最后一层就代表了 125 中最多包含 2 的 6 次方
（ 2**6 < 125 < 2**7 ）
然后每一层都比这一层少 2 倍
所以自上而下从右到左排列余数就是 125 的二进制数表示：1111101

因为我们人类习惯从左到右书写，所以你可以理解为：
从左到右书写就是余数的逆序（自下而上）
取余法图示如下：

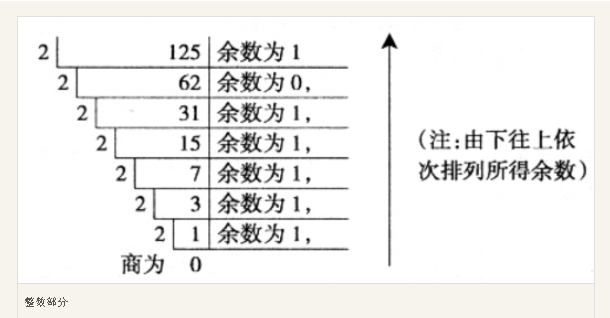
虽然很想把原码，反码，补码都讲透，把小数，负数也都加进去详解，但是实在是时间和精力有限
在此只能解释一下原理，不再写代码了：
1. 原码：
一个二进制位字节（Byte）是 8 位（bit）不可分割的二进制数：00000001 代表十进制数 1
我们规定最左边的一位 0 代表正数  1 代表负数：（这是人为规定，也是为了让计算机能区分正负）
00000001 代表十进制数 1 ； 10000001  代表 -1 
但是按照上面的规定： 00000000 代表 0 ； 10000000 代表 -0  
按照值 0 = -0 ？ 这样对于计算机就会产生歧义，因为一个值有两个表示，而且不利于计算
所以规定：00000000 代表 0  ； 10000000 代表 -128 
这样就意味着一个Byte的值范围： 01111111~10000000 （127~-128）
以上就是原码：
四则运算对我们人来说很简单，因为我们人能轻易的识别各种运算符（+ - * /）等等。
但是计算机不能识别运算符，所以计算机内部只能进行加减的运算。
乘法和除法是可以分解为加法和减法的，但是用原码运算是必须要带符号的：
1-1 = 00000001 + 10000001 = 00000001 - 00000001 = 0
可以看到要先把负数转换为正数，然后相减，这让我们人看的很清晰，但是对计算机是一种浪费

2. 小数：
十进制小数转换为二进制数一般采用 乘 2 取整法：
小数 0.125 举例如下图：	  

3. 反码和补码：
于是根据数学原理，科学家引入了反码和补码，辅助计算机运算
规定正数的原码，反码和补码就是本身。（因为反码和补码是为了负数设计的，方便减法运算）
负数的反码为：符号位不变，按位取反，-1 10000001 反码为 11111110
负数的补码为：反码 +1  -1 的反码为 11111111
1-1 = 00000001 + 11111111 = 100000000（现在得到一个9位的数）  
超出 8 位，直接舍弃超出的值，这样就得到 00000000 = 0
引入反码和补码，就把所有的数学运算全部统一成了加法，这样计算机结构得以简化，效率大大提高

补码的原理：用 -1 举例：

-1 的 原码为： 10000001 这里的最高位 1 代表了负号（-）
-1 的 补码为： 11111111 这里的最高位 1 代表了 -128	

如上图，可以看到引入补码，计算机的二进制运算脱离了正负符号和运算符，只需要加法就可以了

最后贡献一段MD5的加密代码：

加密本质上是定义了一个更深奥的数字范围和进位规则，或者显示规则。

加密和进制其实都只有一个作用就是让人看不懂（开玩笑的）。

仅供参考：

MD5本质上是把我们认识的字符，通过哈希算法给隐藏起来，最后返回一个固定长度的字符串
这样解决了两个问题：
	1. 数字范围太短，容易被遍历算法破解，因为哈希算法加密的是字符串，理论上字符串无尽
	2. 密文太长，导致传输，携带，记忆等等的不方便

# 老规矩导模块，我写的手都快断了！
# 这个没加盐
import hashlib

def encrypt(origin):
    origin_bytes = origin.encode('utf-8')
    md5_object = hashlib.md5()
    md5_object.update(origin_bytes)
    return md5_object.hexdigest()

p1 = encrypt('admin')
print(p1) # "21232f297a57a5a743894a0e4a801fc3"

加盐版：

import hashlib

def encrypt(origin):
    salt = "盐"
    origin_bytes = origin.encode('utf-8')
    md5_object = hashlib.md5(salt.encode("utf-8"))   # 这个地方加盐
    md5_object.update(origin_bytes)
    return md5_object.hexdigest()

p1 = encrypt('admin')
print(p1) # "0956c330a0384f7daa08517619a940c5"