abc233_e Σ[k=0..10^100]floor(X／10^k) 题解

Σ[k=0..10 ^ 100]floor(X／10 ^ k)

题意

给定一个整数 \(x\)，求 \(\sum\limits_{k=0}^{10^{100}} \lfloor \frac{x}{10^k} \rfloor\)。

数据范围

• \(1 \leqslant x \leqslant 10^{500000}\)

思路

看数据范围就知道:long long 存不下，需要高精度。

直接高精度会达到 \(O(|x|^2)\)，也是过不了的。

又要推一下了，画个草图看看。

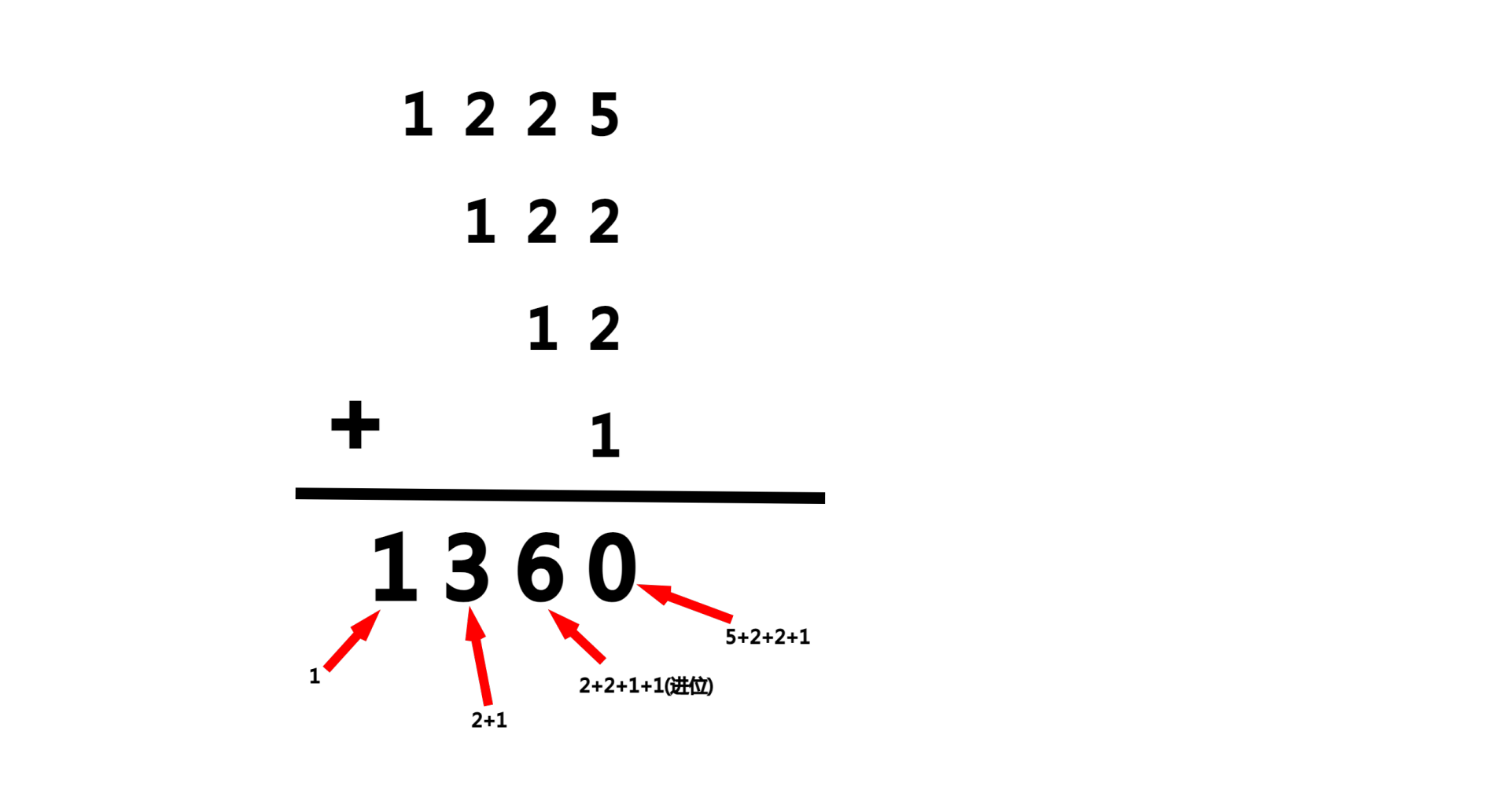
可以发现，在样例1中：

• 个位、十位、百位、千位都可以对答案的个位做出贡献。
• 十位、百位、千位都可以对答案的十位做出贡献。
• 百位、千位都可以对答案的百位做出贡献。
• 千位可以对答案的千位做出贡献。

再稍微推一推，就可以发现：

• 若 \(x = \overline{a_1\ a_2\ a_3\ \dots \ a_n}\)
  • 那么答案就是 \(\sum\limits_{i=1}^{n} (\sum\limits_{j=1}^{n-i+1} a_i \times 10^i)\)

复杂度

• 时间：\(O(|x|)\)
• 空间：\(O(|x|)\)

Code

点击查看代码

#include <iostream>
#include <vector>
#include <string>

using namespace std;

const int N = 6e5 + 10;

string s; // x 太大了，得用字符串
int n, ans[N], sum, lans = 1;

void P () {
  int len = n + 1;
  for (int i = 0; i < len; i++) { // 处理进位
    ans[i + 1] += ans[i] / 10;
    ans[i] %= 10;
  }
  while (len > 1 && !ans[len - 1]) { // 处理前导零
    len--;
  }
  lans = len;
}

void Cout () {
  for (int i = lans - 1; i >= 0; i--) { // 从最高位开始输出
    cout << ans[i];
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> s;
  n = s.size();
  for (int i = 0; i < n; i++) {
    sum += s[i] - '0'; // 前缀和思想
    ans[n - i - 1] = sum; // 去处理答案第 n - i - 1 位（第0位为个位）
  }
  P(); // 最后再处理进位
  Cout();
  return 0;
}