数据结构清华大学出版社顺序表(严蔚敏)(第一次写这个不喜勿喷也是刚入门的小白,希望大佬可以指点一下)
顺序表作为线性结构的一种,而线性结构的特点是:1.存在唯一的一个被称为“第一个”的元素,同时也存在唯一的一个被称为“最后一个”的元素 2、集合之中的每一个元素均有且仅有一个它的前驱或后继。 由此可以得出,作为一种存储数据的方式,如果了解了某种线性结构的存储方式,即可以通过访问结点的前驱和后继达到访问任何一个结点的效果。
作为一种线性存储方式,相邻数据元素之间具有一定的序偶关系,序偶关系意为前驱以及后继元素具有着一定的联系。通常这种联系由顺序表的表示结构来看最为直观。假设以作为顺序表之中的任何一个元素,其唯一的前驱元素为,其唯一的后继元素为。其下标i记作在顺序表之中的位序。
由平时学习的经验可知,了解一类数据结构的基本方法,需要从它的基本结构定义以及基本操作进行入手,所谓的基本结构定义为每一个整体的单位数据元,而相关算法,则是以增加修改删除元素为基础的基本操作函数的集合。下面开始书写顺序表的基本结构定义以及基本操作,这也是平时被称作ADT(抽象数据类型) 的表示方法。
顺序表也可以称作线性表的顺序存储,即使用一组连续的存储单元依次存储线性表的元素,需要注意的是,不同类型的线性表的单位元素大小是不同的,按照已有的认识,表示任何一个元素的存储地址,通过原始的地址加上元素位序与单位元素大小的乘积即可以求出元素的存储地址。两个相邻元素存储位置的关系为:
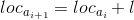
位序为i的元素与位序为0的元素存储位置关系为:
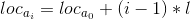
由此,可以看出线性表的顺序存储结构是一种随机存取的存储结构。通常可以用数组来描述该种存储结构,在C语言中可以使用动态存储的一维数组进行表示:
#define LIST_INIT_SIZE 100 //线性表存储空间的初始量分配
#define LISTINCREMENT 10 //线性表存储空间的分配量
#define OK 1
#define ERROR 0
#define OVERFLOW -1
typedef float ElemType;
typedef int Status;
typedef struct{
ElemType *elem;//存储空间基址
Status length;//当前长度
Status listsize;//当前分配的存储容量
}SqList;空表初始化
Status InitList_Sq(SqList &L)//空表初始化
{
//构造一个空的线表L
L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(L.elem==NULL)//判断内存是否分配失败
{
exit(OVERFLOW);
}
L.length=0;//空表长度为0
L.listsize=LIST_INIT_SIZE;//初始存储量(所放的元素个数)
return OK;
}插入一个值
Status ListInsert_Sq(SqList &L,Status i,ElemType e)
{
ElemType *newbase ,*q,*p;
if(i<1||i>L.length)//判断i值是否合法
{
return ERROR;
}
if(L.length>=L.listsize)//判断存储空间是否已满
{
newbase = (ElemType *)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(newbase==NULL)
{
exit(OVERFLOW);//判断是否重新分配成功
}
L.elem=newbase;
L.listsize+=LISTINCREMENT;
}
q=&(L.elem[i-1]);//q为插入位置
for(p = &(L.elem[L.length-1]);p>=q;--p)//p为最后一个元素的位置
{
*(p+1)=*p;//插入元素右移
}
*q = e;
++L.length;
return OK;
} 删除一个值
Status ListDelete_Sq(SqList &L,Status i,ElemType &e)
{
ElemType *p,*q;
//在顺序表中删除第i个元素并用e返回结果
if((i<1)||(i>L.length))//判断i值是否合法
{
return ERROR;
}
p = &(L.elem[i-1]);//p为删除的位置
e = *p;//把删除的元素的值给e
q = L.elem+L.length-1; //表尾元素的位置
for(++p;p<=q;++p)
{
*(p-1)=*p;//被删除的元素之后左移
}
--L.length;
return OK;
}对线性表进行查找
Status LocateElem_Sq(SqList L,ElemType e)
{
//在顺序表中查询第一个满足判定条件的数据元素
//若元素存在则返回它的位序,否则则返回0
Status i;//i的初始值为第一个元素的位序
i=1;
while(i<=L.length&&L.elem[i-1]!=e)
{
++i;
}
if(i<=L.length)
{
return i;
}
else
{
return 0;
}
}对俩个顺序表进行合并
void MergeList_Sq(SqList La,SqList Lb,SqList &Lc)
{
ElemType *pa,*pb,*pc,*pa_last,*pb_last;
//已知线性表的元素按递增元素排序
//归并La和Lb得到新表Lc
pa=La.elem;
pb=Lb.elem;
Lc.listsize=Lc.length=La.length+Lb.length;
pc=Lc.elem=(ElemType *)malloc(Lc.listsize*sizeof(ElemType));
if(!Lc.elem)//判断是否分配失败
{
exit(OVERFLOW);
}
pa_last=La.elem+La.length-1;
pb_last=Lb.elem+Lb.length-1;
while((pa<=pa_last)&&(pb<=pb_last))
{
if(*pa<=*pb)
{
*pc++=*pa++;
}
else
{
*pc++=*pb++;
}
}
while(pa<=pa_last)//将a中剩余的元素复制到c中
{
*pc++=*pa++;
}
while(pb<=pb_last)//将b中剩余的元素复制到c中
{
*pc++=*pb++;
}
}运行截图

下面是完成的代码:可以免费下载
代码下载
别废话,拿你代码给我看。


