Solr相似度名词：VSM(Vector Space Model)向量空间模型

最近想学习下Lucene ，以前运行的Demo就感觉很神奇，什么原理呢，尤其是查找相似度最高的、最优的结果。索性就直接跳到这个问题看，很多资料都提到了VSM（Vector Space Model）即向量空间模型，根据这个模型可以对搜索的结果进行最优化的筛选，目前还不知道如何证明，只能凭借想象应该是这个样子的。

1、看一下TF/IDF

我们先来看下一个叫TF/IDF的概念，一般它用来作为一个搜索关键字在文档或整个查询词组的权重的计算方式。前几天看了吴军老师的数学之美系列文章，这个TF/IDF可以追溯到信息论中的相对熵的概念。在有些文献中它被称为成“交叉熵”。在英语中是 Kullback-Leibler Divergence，是以它的两个提出者库尔贝克和莱伯勒的名字命名的。相对熵用来衡量两个正函数是否相似，对于两个完全相同的函数，它们的相对熵等于零。在自然语言处理中可以用相对熵来衡量两个常用词（在语法上和语义上）是否同义，或者两篇文章的内容是否相近等等。利用相对熵，我们可以到处信息检索中最重要的一个概念：词频率-逆向文档频率（TF/IDF)。

影响一个词(Term)在一篇文档中的重要性主要有两个因素：
• Term Frequency (tf)：即此Term在此文档中出现了多少次。tf 越大说明越重要。
• Document Frequency (df)：即有多少文档包含次Term。df 越大说明越不重要。
容易理解吗？词(Term)在文档中出现的次数越多，说明此词(Term)对该文档越重要，如“搜索”这个词，在本
文档中出现的次数很多，说明本文档主要就是讲这方面的事的。然而在一篇英语文档中，this出现的次数更多，
就说明越重要吗？不是的，这是由第二个因素进行调整，第二个因素说明，有越多的文档包含此词(Term), 说明
此词(Term)太普通，不足以区分这些文档，因而重要性越低。

道理明白了，我们来看看公式：

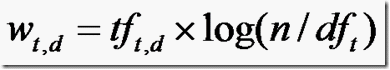
W(t,d):the weight of term t in document d

tf(t,d):frequency of term t in document d

n :total number of documents

df(t):the number of documents that contain term t

一些简单的模型(Term Count Model)忽略了文档的总数这个变量，那样权重的计算就是 $w_{t,d} = \mathrm{tf}_{t,d}$ (In a simpler Term Count Model the term specific weights do not include the global parameter. Instead the weights are just the counts of term occurrences: $w_{t,d} = \mathrm{tf}_{t,d}$ .)

2、进入VSM

我们把文档看作一系列词(Term)，每一个词(Term)都有一个权重(Term weight)，不同的词(Term)根据自己在
文档中的权重来影响文档相关性的打分计算。
于是我们把所有此文档中词(term)的权重(term weight) 看作一个向量。
Document = {term1, term2, …… ,term N}
Document Vector = {weight1, weight2, …… ,weight N}
同样我们把查询语句看作一个简单的文档，也用向量来表示。
Query = {term1, term 2, …… , term N}
Query Vector = {weight1, weight2, …… , weight N}
我们把所有搜索出的文档向量及查询向量放到一个N维空间中，每个词(term)是一维。

我们认为两个向量之间的夹角越小，相关性越大。
所以我们计算夹角的余弦值作为相关性的打分，夹角越小，余弦值越大，打分越高，相关性越大。

我们只要比较下图中的α,θ的余弦值的大小，余弦值越大，相似度越高。公式如下：

$\mathrm{sim}(d_j,q) = \frac{\mathbf{d_j} \cdot \mathbf{q}}{\left\| \mathbf{d_j} \right\| \left \| \mathbf{q} \right\|} = \frac{\sum _{i=1}^N w_{i,j}w_{i,q}}{\sqrt{\sum _{i=1}^N w_{i,j}^2}\sqrt{\sum _{i=1}^N w_{i,q}^2}}$

下面列出计算方法：

设d1=(x1,y1),q=(x2,y2)

我们根据余弦定理，cos(α)=cos(A-B)

=cos(A)cos(B)+sin(A)sin(B)

=(x1/sqr(x1*x1+y1*y1))(x2/sqr(x1*x1+y1*y1))+(y1/sqr(x1*x1+y1*y1))(y2/sqr(x1*x1+y1*y1))

合并同类项，即向量d1与向量q的内积/向量模，也即上面的公式sim(dj,q)。

举个例子，查询语句有11个Term，共有三篇文档搜索出来。其中各自的权重(Term weight)，如下表格。

t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11
D1 0 0 0.477 0 0.477 0.176 0 0 0 0.176 0
D2 0 0.176 0 0.477 0 0 0 0 0.954 0 0.176
D3 0 0.176 0 0 0 0.176 0 0 0 0.176 0.176
Q 0 0 0 0 0 0.176 0 0 0.477 0 0.176

于是计算，三篇文档同查询语句的相关性打分分别为：

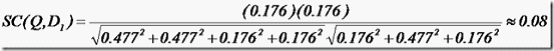
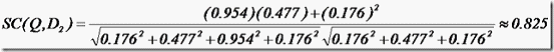
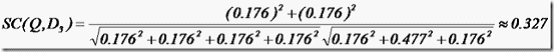
于是文档二相关性最高，先返回，其次是文档一，最后是文档三。

参考：

1)tf/idf：http://en.wikipedia.org/wiki/Tf-idf

2)vsm：http://en.wikipedia.org/wiki/Vector_space_model wikipedia维基百科

4)网络资料：http://forfuture1978.javaeye.com

posted @ 2015-06-15 18:08 lvyafei 阅读(587) 评论(0) 编辑收藏举报

刷新页面返回顶部

lvyafei

Solr相似度名词：VSM(Vector Space Model)向量空间模型

公告