电信用户流失分析与预测

@

目录

• 一. 研究背景
• 二. 分析结论与建议
• 三. 任务与实现
• 四. 数据集解析
• 五. 数据分析套餐
  • 1.准备工作
    • 导入相关的库
    • 导入数据集
  • 2.数据预处理
    • 类型转换
    • 缺失值处理
    • 重复值处理
  • 3.查看流失情况
  • 4.类别特征的描述性分析
  • 5.连续型变量的分析
    • 差异检验-两样本t检验
    • 分箱离散化
  • 6.机器学习
    • 基模型的建立
    • 基模型的初始评分
    • 异常值处理
    • 数据标准化处理
    • 样本不均衡处理&逻辑回归
    • 网格交叉验证&KNN
    • 决策树
    • 流水线&朴素贝叶斯
    • 多层感知器
    • 模型得分总结

这是作者自己做的一个数据分析项目，闲暇时间陆陆续续耗时大约2周，通篇采用大量python源码编写，欢迎一起学习交流，提升自我。
我的CSDN地址：https://blog.csdn.net/weixin_46274061/article/details/107790605
转载请标明出处，谢谢！
数据集下载地址：https://www.datafountain.cn/datasets/35guide

一. 研究背景

用户流失预测在机器学习中算是一种比较典型的分类场景，做好用户的流失预测可以降低营销成本，留住用户并且获得更好的用户体验，在三大巨头的瓜分下，做好营销运营比重新获取一个新用户更节省成本。达到较好的运营回报。如果在传统分类模式下，通常是通过人工对各个特征进行统计，然后分到合适的类别中，这样不但会耗费大量的资源，且低效。

二. 分析结论与建议

1. 增加套餐福利，解锁更多权益，如赠送流量，免费看视频，增设小游戏，贵族制度，
2. 加强电话服务质量，设立评分反馈系统，及时跟踪异常评分
3. 加强光纤相关设施的建设，增强网络稳定性
4. 鼓励用户开通各种服务，如在线安全，在线备份，设备保护，技术支持
5. 增加充值返现，充值满减，发放优惠券的方式，用户消费达到一定金额解锁特权
6. 针对老年人建议赠送通话时长，提高活跃度
7. 针对排名前十的职业根据相应的职业给予相应的优惠和福利，提高用户的粘性。

三. 任务与实现

我们的任务在于：
1.分析出流失用户有哪些显著性特征？
2.找出哪些用户容易流失？
具体实现内容包括：
能够对数据进行数据预处理 包括缺失值，异常值，重复值
能够描述性分析各个特征与流失用户的占比是否显著
能够将连续型变量进行分箱离散化
能够将离散型特征进行独热编码
能够建立基模型，将源数据进行标准化
能够处理样本不均衡
能够熟练运用多种分类模型对电信用户进行预测
分析模型有：逻辑回归，KNN，朴素贝叶斯，决策树，多层感知器。

四. 数据集解析

每行代表一个客户，每列包含元数据列中描述的客户属性。
一共7043行数据，21个列。前20个为特征列，最后一个为研究对象。
1 customerID Integer ：用户ID
2 gender String：性别（Female or Male）
3 SeniorCitizen Integer： 老年人(1表示是，0表示不是)
4 Partner String：配偶(Yes or No)
5 Dependents String：家属(Yes or No)
6 tenure Integer ：职位(0~72，共73个职位)
7 PhoneService String：电话服务（Yes or No）
8 MultipleLines String：多线（Yes 、No or No phoneservice 三种）
9 InternetService String：互联网服务（No, DSL数字网络，fiber optic光纤网络 三种）
10 OnlineSecurity String：在线安全（Yes，No，No internetserive 三种）
11 OnlineBackup String：在线备份（Yes，No，No internetserive 三种）
12 DeviceProtection String：设备保护（Yes，No，No internetserive 三种）
13 TechSupport String：技术支持（Yes，No，No internetserive 三种）
14 StreamingTV String：网络电视（Yes，No，No internetserive 三种）
15 StreamingMovies：网络电影 （Yes，No，No internetserive 三种）
16 Contract String：合同（Month-to-month，One year，Two year 三种）
17 PaperlessBilling String：账单（Yes or No）
18 PaymentMethod String：付款方式（bank transfer，credit card，electronic check，mailed check 四种）
19 MonthlyCharges Integer ：月费用
20 TotalCharges Integer ：总费用
21 Churn String：流失（Yes or No）

五. 数据分析套餐

1.准备工作

本文数据源来自网上，数据源除了各大网站可以下载，还可以来自自家公司的数据库，爬虫等方式获取。

导入相关的库

# 导入库 
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns
import warnings
from matplotlib import font_manager
import time

sns.set(style="darkgrid", font_scale=1.2)
# plt.rcParams["font.family"] = "SimHei"
plt.rcParams['font.family'] = ['Arial Unicode MS']
plt.rcParams["axes.unicode_minus"] = False
my_font=font_manager.FontProperties(fname=
                                    '/System/Library/Fonts/PingFang.ttc',
                                    size=15)  
warnings.filterwarnings("ignore")

from scipy import stats #用于方差分析

# from sklearn.linear_model import LinearRegression  #线性回归模型
from sklearn.model_selection import train_test_split #切分训练集 测试集
from sklearn.linear_model import LogisticRegression #逻辑回归模型
from sklearn.metrics import classification_report #混淆矩阵打分
from sklearn.model_selection import GridSearchCV #网格交叉验证
from imblearn.over_sampling import SMOTE,ADASYN # 引入SMOTE和ADASYN处理样本不均衡
from collections import Counter #查看每个类别出现的次数
from sklearn.pipeline import Pipeline #引入流水线
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # 评估指标 --正确率 精准率 召回率 F1调和平均值
from sklearn.neighbors import KNeighborsClassifier #KNN分类模型
from sklearn.preprocessing import StandardScaler, MinMaxScaler # StandardScaler：均值标准差标准化 # MinMaxScaler：最小最大值标准化
from sklearn.neural_network import MLPClassifier #多层感知器

导入数据集

data = pd.read_csv("WA_Fn-UseC_-Telco-Customer-Churn.csv")
print(data.shape)
data.sample(10)

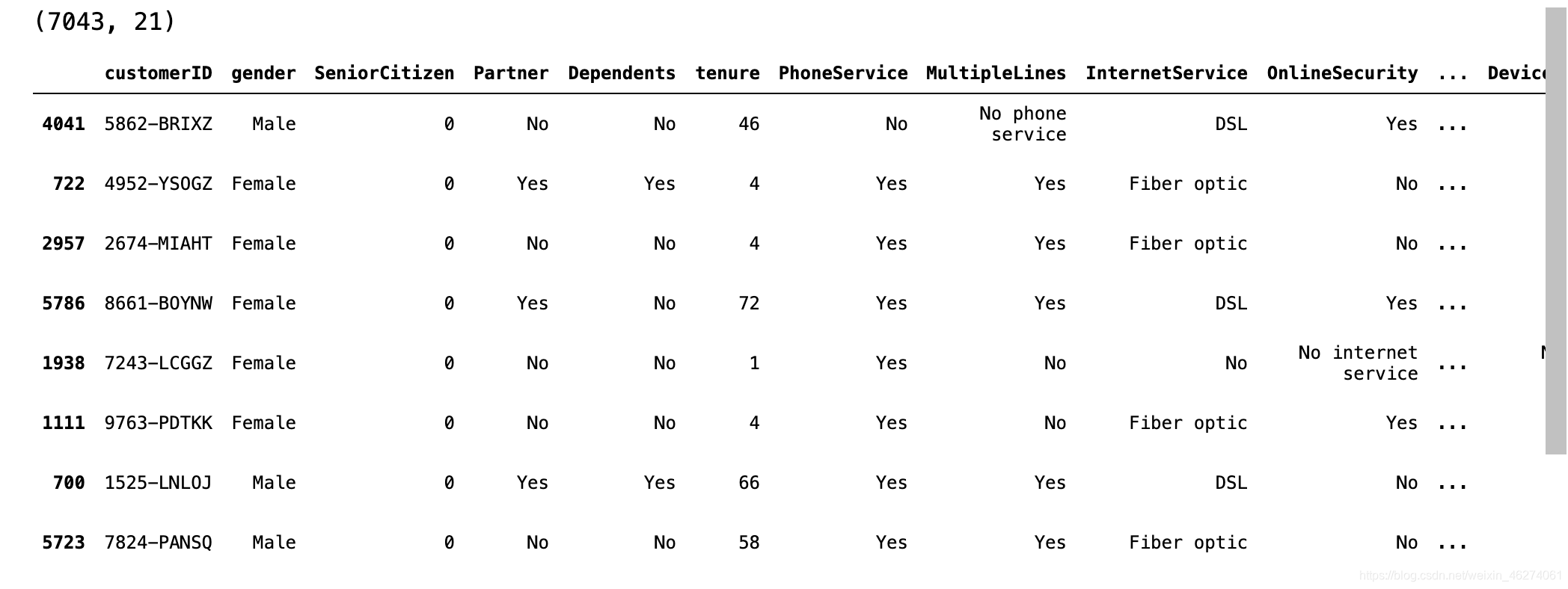
2.数据预处理

查看数据整体情况

data.info()

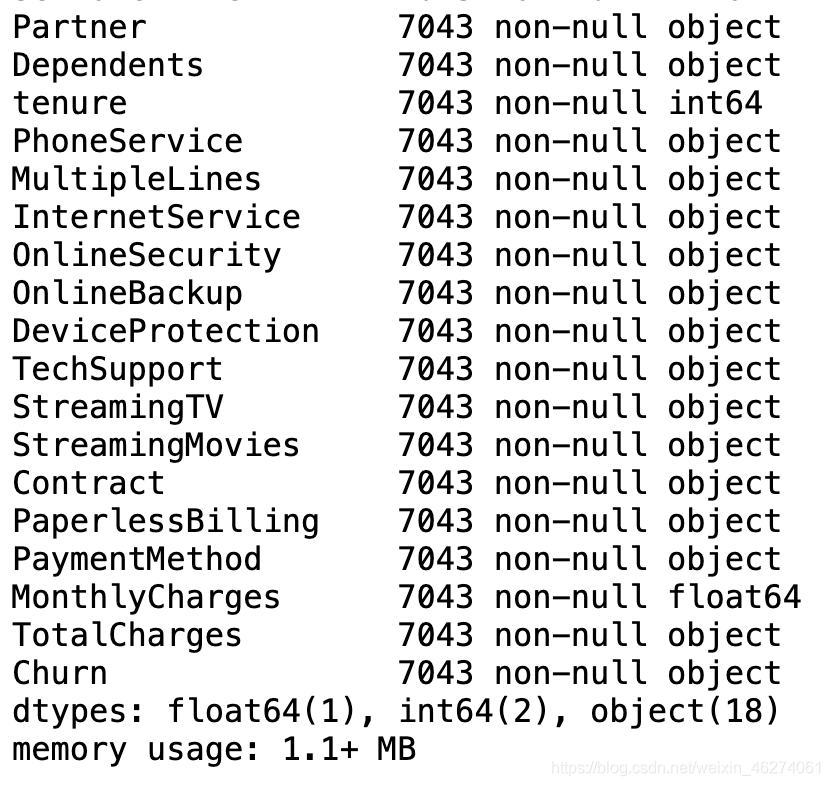
类型转换

我们发现TotalCharges本应该是float64类型，这里却是object类型，那么需要转换。

data['TotalCharges'].astype(np.float64)

会报错 无法转换。这里用到一个函数：DataFrame.convert_objects( convert_dates = True，convert_numeric = False，convert_timedeltas = True，copy = True )

data["TotalCharges"]=data["TotalCharges"].convert_objects(convert_numeric=True)
data['TotalCharges'].dtype

输出：dtype('float64') ，转换完成。

缺失值处理

data.isnull().sum(axis=0)

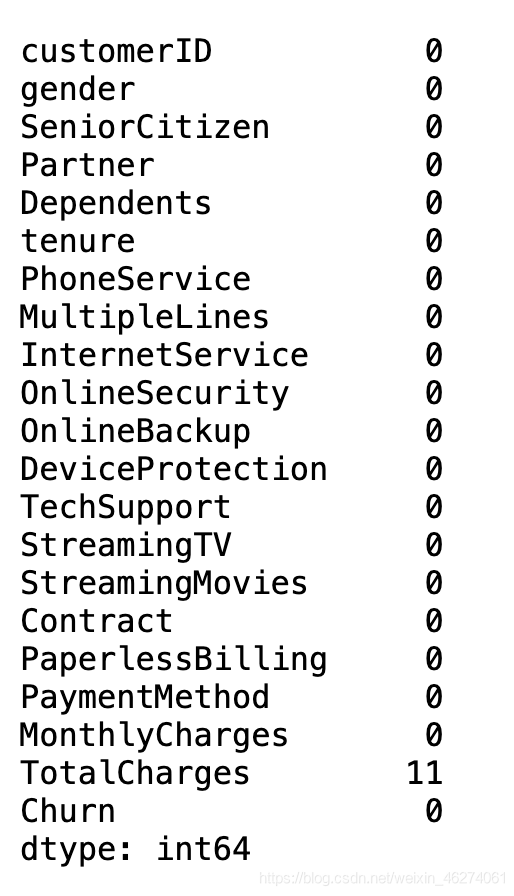
TotalCharges有11个缺失值，查看数据分布 再确定是删除还是填充

print(data["TotalCharges"].skew()) 
sns.distplot(data["TotalCharges"].dropna())

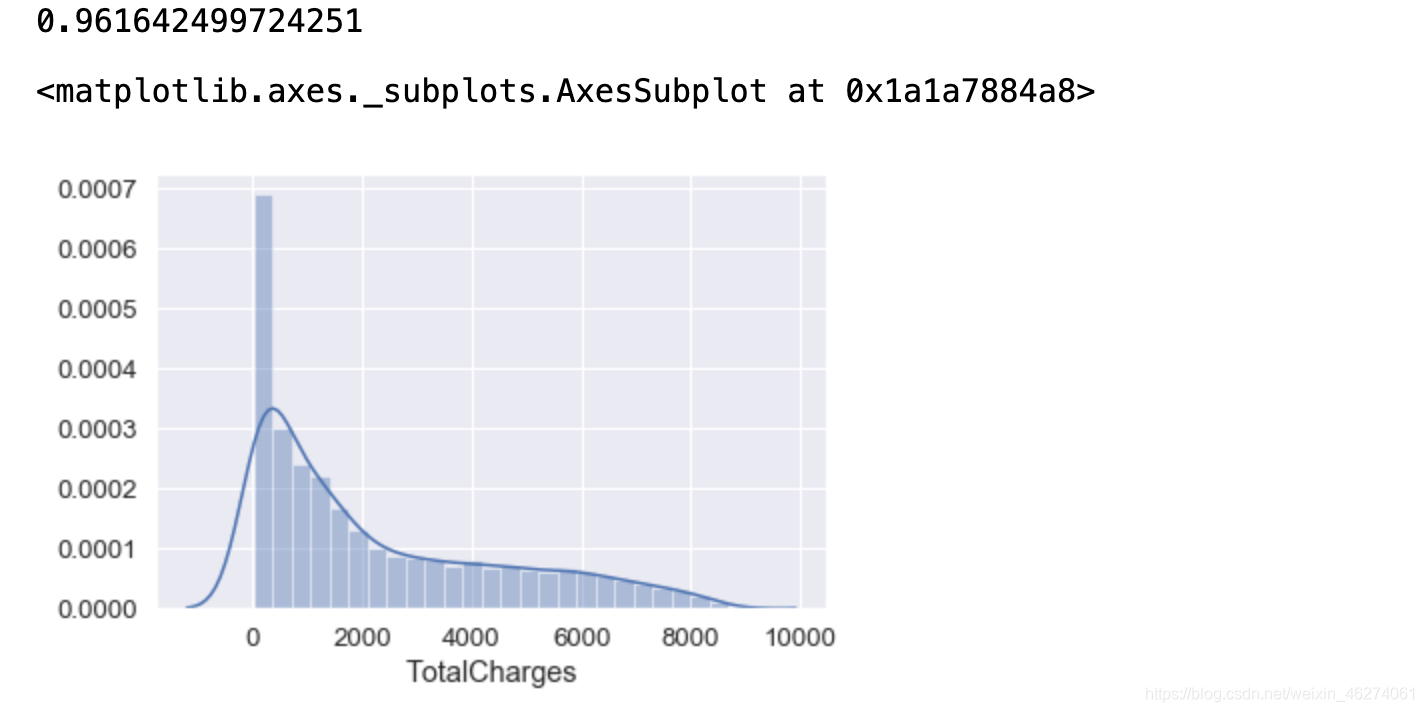
结果大于0, 属于右偏 ,当然 ,也能一眼从图形看出。
缺失值的处理方式有：删除，中位数填充，均值填充，众数填充。
右偏数据我们用中位数填充，两种方式计算中位数，计算中位数时会剔除缺失值

data["TotalCharges"].median()
或者
np.median(data["TotalCharges"].dropna().values)

输出为：1397.475

填充缺失值

data.fillna({"TotalCharges":data["TotalCharges"].median()},inplace=True)
data.isnull().sum(axis=0)

重复值处理

如果有重复值：可直接删除

# data.drop_duplicates(inplace=True)
data.duplicated().sum()

输出：0
说明没有重复值

3.查看流失情况

整体流失情况 条形图查看

Churn_value=data["Churn"].value_counts()
display(Churn_value)
sns.countplot(x="Churn",data=data)

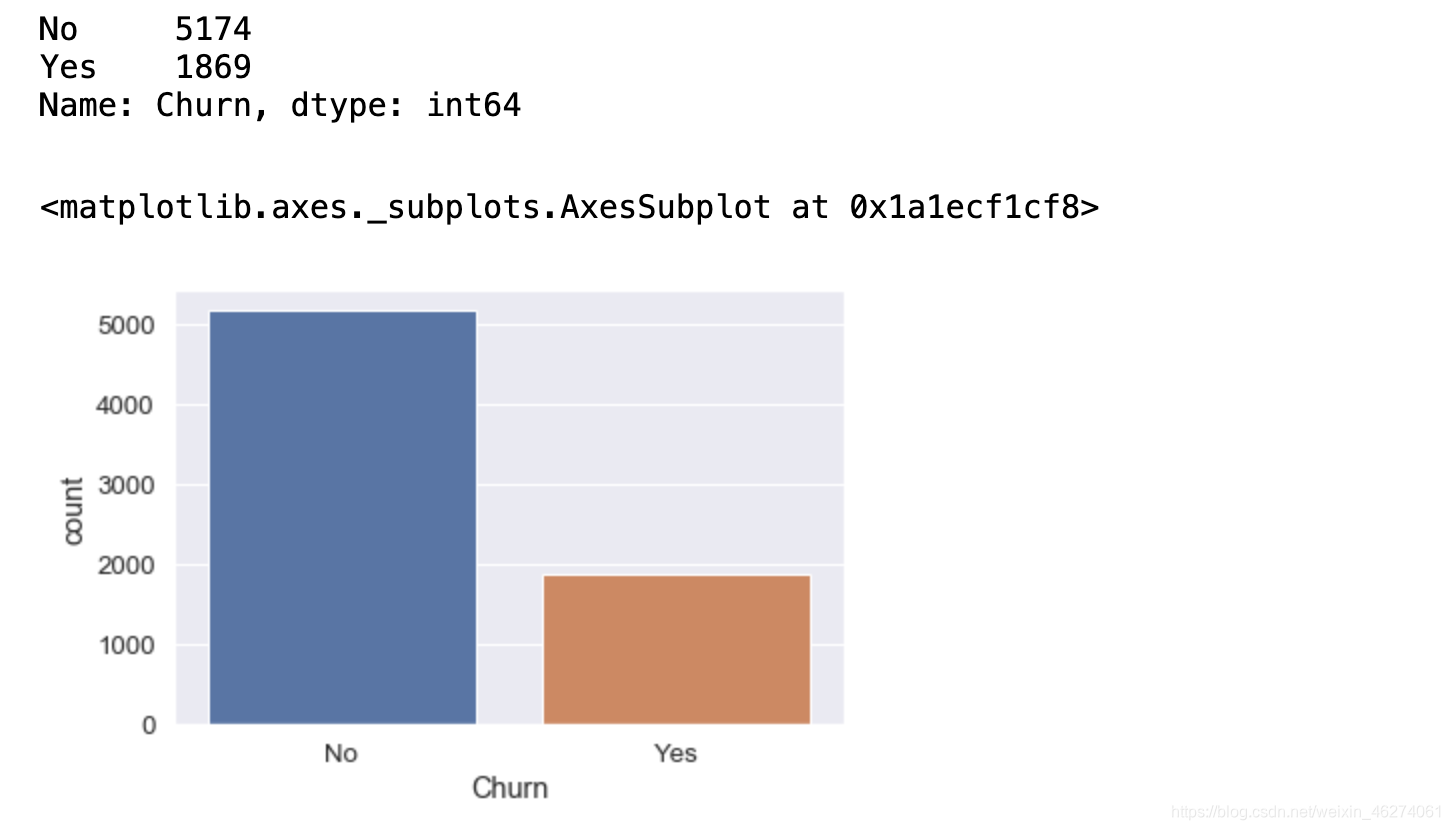
也可饼状图查看

size=Churn_value.values
label_list=Churn_value.index
color=["#009999","#FF7400"]
explode=[0,0.1]
plt.figure(figsize=(8,8),dpi=80)
patches,l_text,p_text=plt.pie(size,
                            explode=explode,
                            colors=color,
                            labels=label_list,
                            labeldistance=1.1,
                            autopct='%1.1f%%',   
                            shadow=True,
                            startangle=90,
                            pctdistance=0.6,
                            )  
plt.show()

饼状图可以内部直接算出百分比，从图中可以看出流失比例26.5%，占比较高，也处于样本不均衡问题，后面可以采用过采样来解决，过采样相比欠采样较稳定。

对于研究对象:Churn,我们用pandas中的map函数实现数字化处理，我们通常将关注的类别设为1。

data["Churn"]=data["Churn"].map({"Yes":1,"No":0})
data.head()

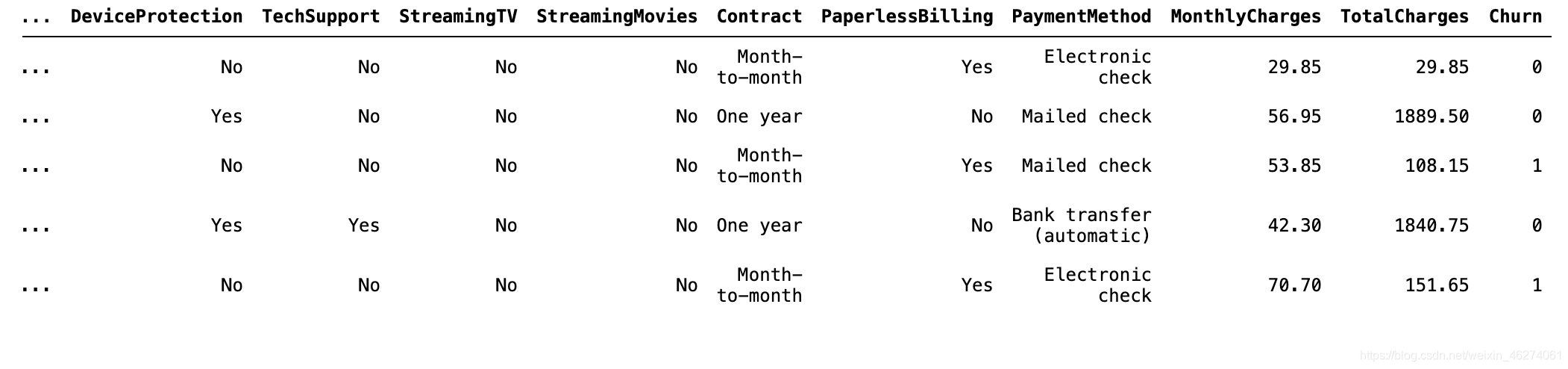
可以看出已经成功的将Churn做了离散化处理。

4.类别特征的描述性分析

特征列主要分两大阵容，类别变量和连续型变量，我们有两种方式把他们分离出来，第一种是直接一个一个drop掉，第二种方法是采用pandas里面提供的判断类别类型和数值型的方法，这里我们采用第二种方式。

data_columns=[]
for col in data.columns.drop(["customerID","Churn"]):
    # is_object_dtype：查看特征是否为类别类型，是的话往下执行；
    # is_numeric_dtype：查看类别是否是数值类型的，是的话就继续往下
    if pd.api.types.is_object_dtype(data[col]):
        data_columns.append(col)
print(data_columns)
data_object_lens=len(data_columns)

plt.figure(figsize=(20,100))#,dpi=80)
for col,k in zip(data_columns,range(data_object_lens)):
    # 子图第一列
    plt.subplot(data_object_lens,2,2*k+1)
    plt.title("Churn by "+col)
    t=sns.countplot(x=col,hue="Churn",data=data) #内部可统计数量
    t.set_ylabel('数量')
    

    # 子图第二列
    plt.subplot(data_object_lens,2,2*k+2)
    plt.title("Churn rate by "+col)
    #内部可计算均值 相当于所有1相加再除以总数就等于流失率
    sns.barplot(x=col,y="Churn",data=data).set_ylabel("流失率") 
    # 分组计算流失率
    print(data.groupby(by=col)["Churn"].mean())

输出如下：




从图中可以看出：
gender性别对于流失占比分布较均衡，无显著性差异；
Partner无配偶的流失率相对有配偶的流失率高13%；
Dependents无家属相对有家属的流失率高16%；
PhoneService有电话服务的用户量非常巨大，流失率占到了接近三成；
MultipleLines多线业务对流失率无显著性差异；
InternetService互联网服务中fiber optic光纤网络用户群体约占所有用户的1/3，流失率占比却超过了光纤用户的40%；
OnlineSecurity无在线安全的用户量不仅巨大，流失率也超过40%；
OnlineBackup无在线备份功能的用户中，40%会流失；
DeviceProtection无设备保护的用户比有保护的用户流失率高17%；
TechSupport无技术支持的用户中 有4成会流失；
StreamingTV网络电视的有无对流失率无显著性差异；
Streaming网络电影的有无对流失率无显著性差异；
Contract合同按月的用户占比最多，其中，流失率达到了42%，一年签的用户中流失率只占1成，两年签的几乎不会流失；
PaperlessBilling有账单的用户流失率高于无账单的17%；
PaymentMethod付款方式中电子支票的用户中，流失率快达到一半人数。

运营建议：

1. 针对单身用户和无家属用户，他们最大的相同点就是容易产生孤独感，社交较薄弱，可以给这类人群增加套餐福利，如单身贵族等级制度，赠送流量刷剧看视频，小游戏等方式可提高会员等级，达到一定等级解锁新权益，让用户心理有赚到的感觉。
2. 电话服务质量是否存在一定问题，客服人员服务态度是否亲和，若没有，定期做相关培训。是否真实的帮助用户解决了，设立电话服务后的评分反馈系统，若评分较低再次跟进直到真实的帮助到了用户。
3. 现在用户很大部分愿意选择用光纤，说明都有意识到它的快速便捷，但是真实情况是经常网络不稳定，所以可以加大力度对这方面设施设备的建设。
4. 鼓励用户开通在线安全，在线备份，设备保护，技术支持。
5. 有账单和电子支票的用户极大部分是对价格比价敏感，考虑到有的用户经济不独立，比如学生，而且合同中按月支付容易流失极大可能是无法承担费用造成的，我们可以采取鼓励按年签约，校园套餐，每月返现的方式，充值满减，发放优惠券，消费达到一定金额提升会员等级解锁特权。

除了以上特征，发现SeniorCitizen老年人和tenure职业还有遗漏。
对于老年人代码分析如下：

plt.figure(figsize=(20,13))#,dpi=80)
plt.subplot(2,2,1)
sns.countplot(x="SeniorCitizen",hue="Churn",data=data)

plt.subplot(2,2,2)
t=sns.barplot(x="SeniorCitizen",y="Churn",data=data)
t.set_ylabel("流失率")
t.set_title("老年人与流失率的关系")
print(data.groupby(by="SeniorCitizen")["Churn"].mean())

老年人数量虽然占比不高，但是流失率却高达41%，但是其他用户都会向这个群体迈入，很多老年人只会用打电话这一功能，所以我们可以采取启用亲友电话卡绑定，提高老年人群体的免费拨打时长，增加短信提示每月剩余通话时长，提高活跃度。

对于职业，代码分析如下：

plt.figure(figsize=(100,40))
sns.countplot(x="tenure",hue="Churn",data=data)

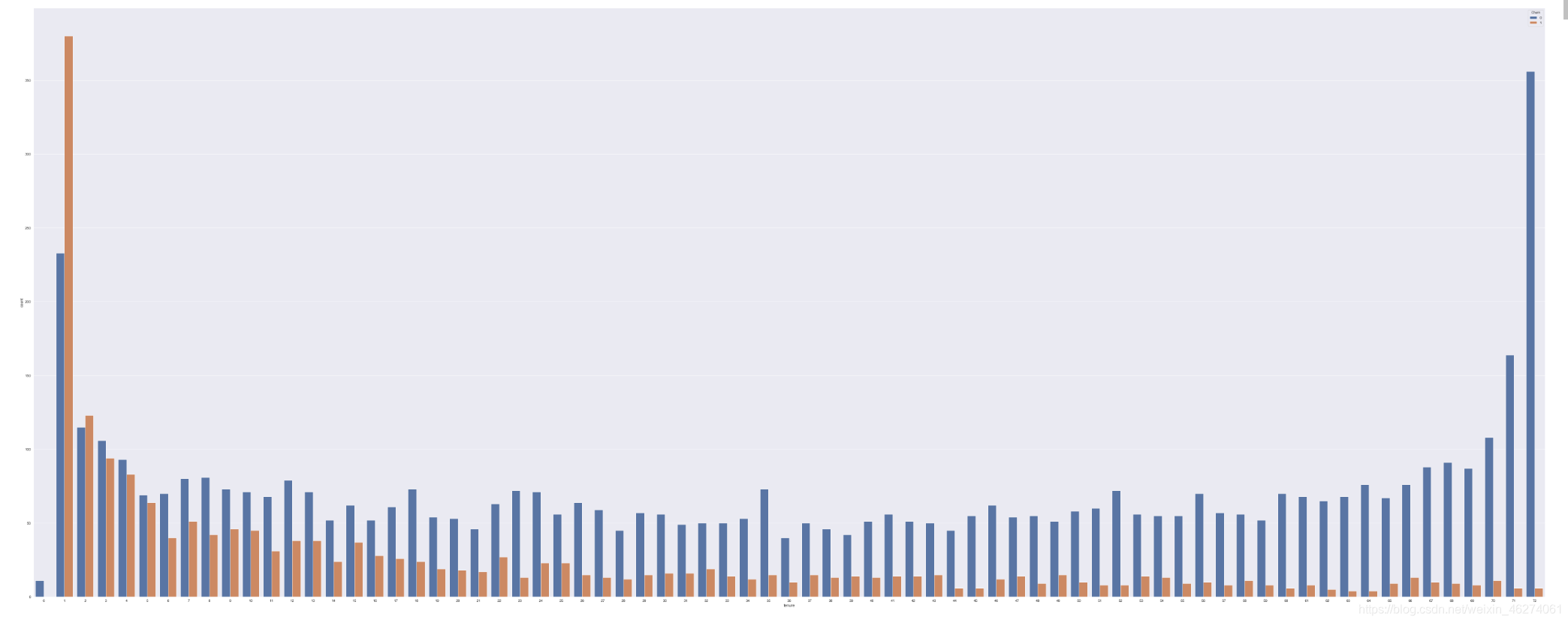
职业中：不同的数字代表不同的职业，挑选出了流失率排前十的职业。

plt.figure(figsize=(100,20))
t=sns.barplot(x="tenure",y="Churn",data=data)
t.set_title("不同职业与流失率的关系",size=100,color="#009999")
data.groupby(by="tenure")["Churn"].mean().sort_values(ascending=False).iloc[:10,]

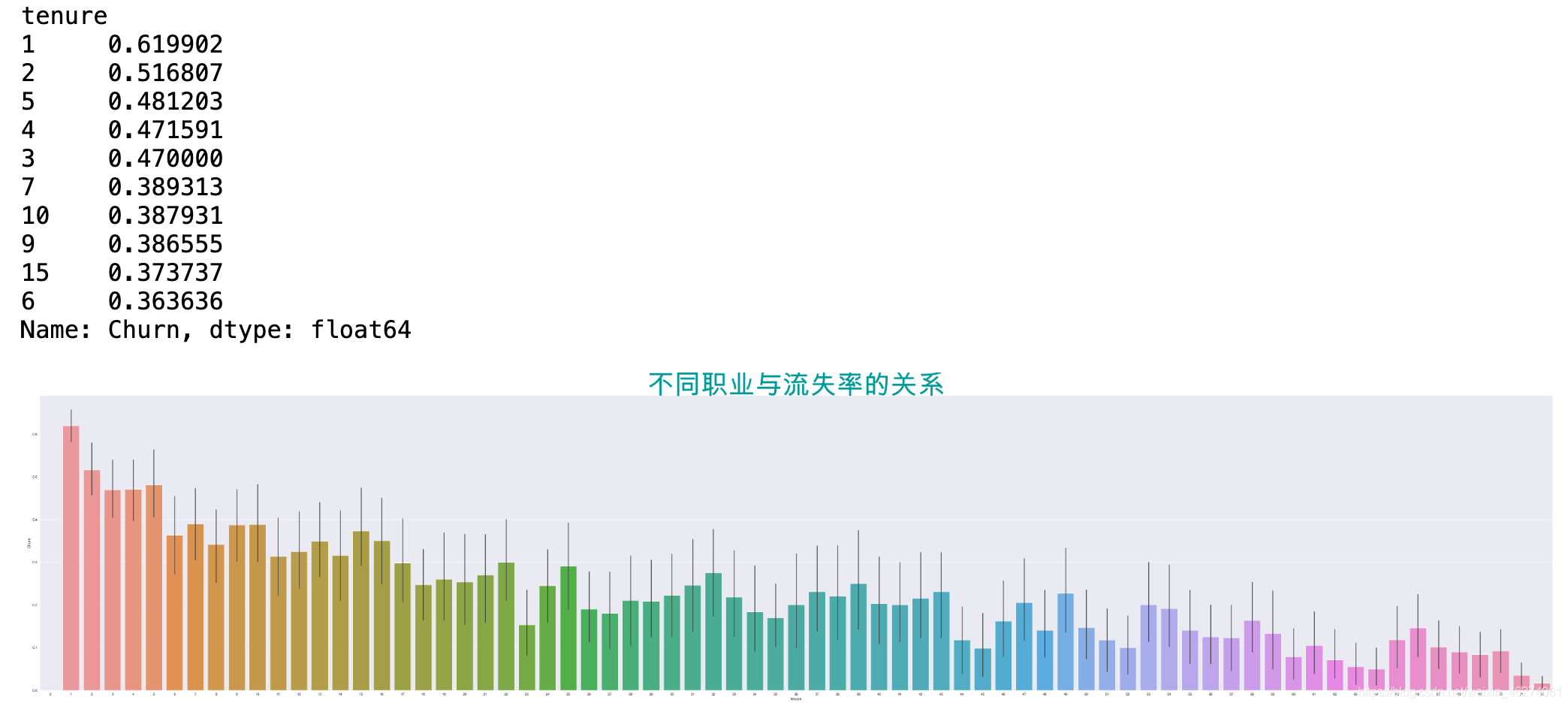
从两个图结合可以看出，不同职业跟流失率也会存在一定的关系，职业为’0‘的虽然人数少，但是流失率几乎为0，职业为’1‘的人数不仅最多，流失率也超过了该职业的50%。流失率排名前十的职业分别为：1，2，5，4，3，7，10，9，15，6。
办法建议：可以采取奖励机制。

5.连续型变量的分析

连续型变量：MonthlyCharges（月消费）和TotalCharges（总消费）
从主观上来看，用户的消费价格都是比较敏感的，所有我们可以重点关注一下消费价格。
查看月消费和总消费的各分位数 数据分布情况：

data.loc[:,["MonthlyCharges","TotalCharges"]].describe()

在7043条数据中，用户月消费的平均水平在65元，中位数在70元，最小消费为18元，最大消费为118元；
总消费的的平均水平在2282元，中位数在1397元，最小消费为18元，最大消费为8684元。
其中，月消费的平均值比中位数略小，主要受极小值的影响；总消费的平均值高于中位数885元，主要受到一些极大值影响。

我们可以具体分别查看月消费，总消费各排名前十的用户信息。
首先查看月消费最低的10名用户：

data.sort_values(by="MonthlyCharges",ascending=True).iloc[:10]

查看月消费最大的10名用户：

data.sort_values(by="MonthlyCharges",ascending=True).iloc[-10:]

总消费最小的10名用户：

data.sort_values(by="TotalCharges",ascending=True).iloc[:10]

查看总消费最高的10名用户：

data.sort_values(by="TotalCharges",ascending=True).iloc[-10:]

高消费的明显特征是他们都有这些服务的需求，不易流失；
低消费的明显特征恰恰相反，他们没有这些需求，猜测与养号有关。

用散点图查看流失用户整体分布

plt.figure(figsize=(20,8),dpi=80)
sns.scatterplot(x="MonthlyCharges",y="TotalCharges",color="g",data=data[data["Churn"]==0])
sns.scatterplot(x="MonthlyCharges",y="TotalCharges",color="r",data=data[data["Churn"]==1])

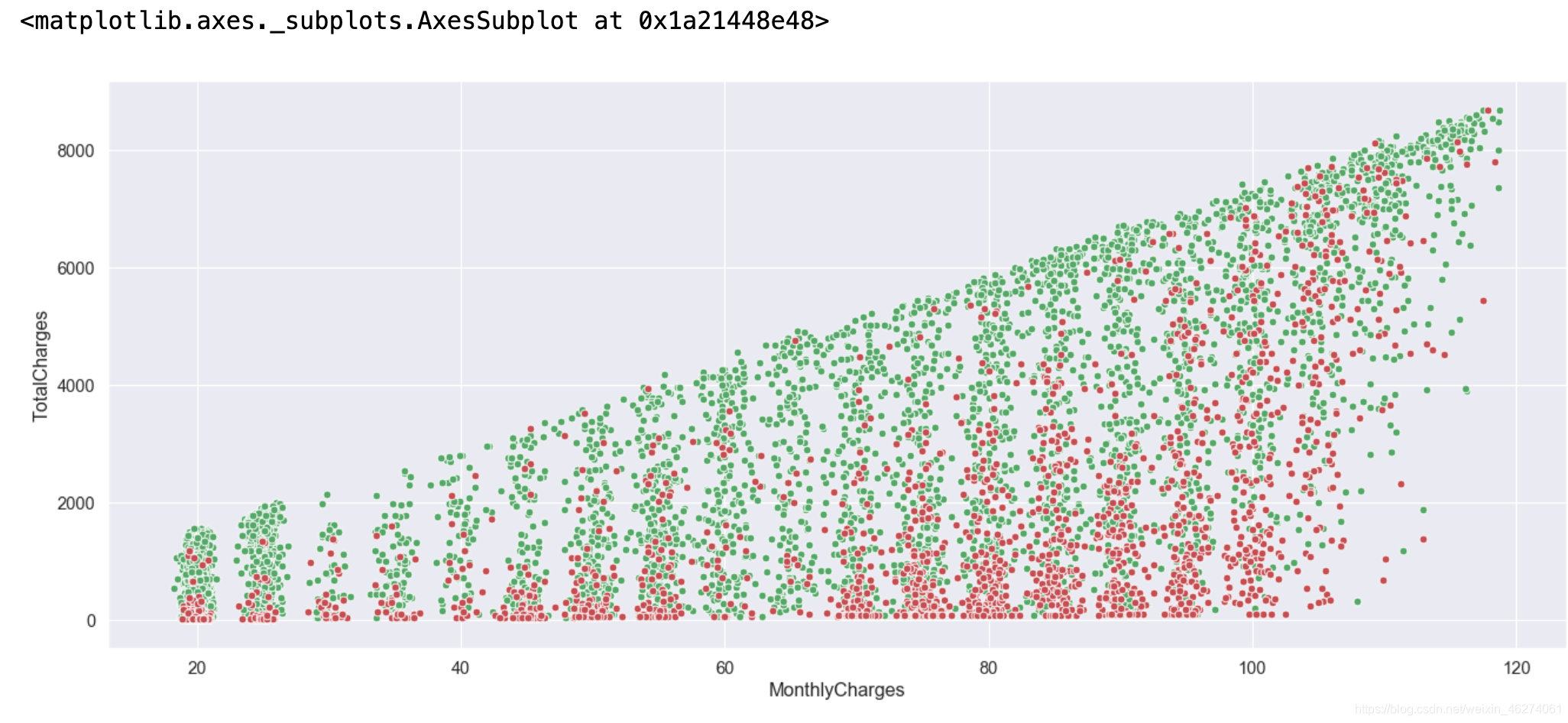
红色代表流失用户，从图中可以看出流失用户主要分布在总消费偏低以及月消费偏高的地方。

尝试用条形的散点图查看分布情况：

fig=plt.figure(figsize=(20,10),dpi=80)
# 子图1
fig.add_subplot(2,2,1)
sns.stripplot(x="Churn",y="MonthlyCharges",data=data)
plt.title('月消费与流失的关系',fontproperties=my_font,color='red')

# 子图2
fig.add_subplot(2,2,2)
sns.stripplot(x="Churn",y="TotalCharges",data=data )
plt.title("总消费与流失的关系")
plt.show()

似乎不是很好看，哈哈~
蜂群图：本来想展示一下蜂群图查看分布情况，但是太丑了就略过。

条形图：

fig=plt.figure(figsize=(20,10),dpi=80)
# 子图1
fig.add_subplot(2,2,1)
# 分组计算流失与否的均值
display(data.groupby("Churn")["MonthlyCharges"].mean())
# barplot内部会自己求均值
sns.barplot(x="Churn",y="MonthlyCharges",data=data)
# 图中那条线代表总体均值所在的置信区间 默认为95%的置信度

# 子图2
fig.add_subplot(2,2,2)
display(data.groupby("Churn")["TotalCharges"].mean())
sns.barplot(x="Churn",y="TotalCharges",data=data)
plt.show()

样本中流失用户的月消费平均值为74元，未流失用户的月消费均值为61元；流失用户的总消费均值为1531元，未流失用户的均值为2552元。

箱线图：

fig=plt.figure(figsize=(20,10),dpi=80)
# 子图1
fig.add_subplot(2,2,1)
sns.boxplot(x="Churn",y="MonthlyCharges",data=data)

# 子图2
fig.add_subplot(2,2,2)
sns.boxplot(x="Churn",y="TotalCharges",data=data)
plt.show()

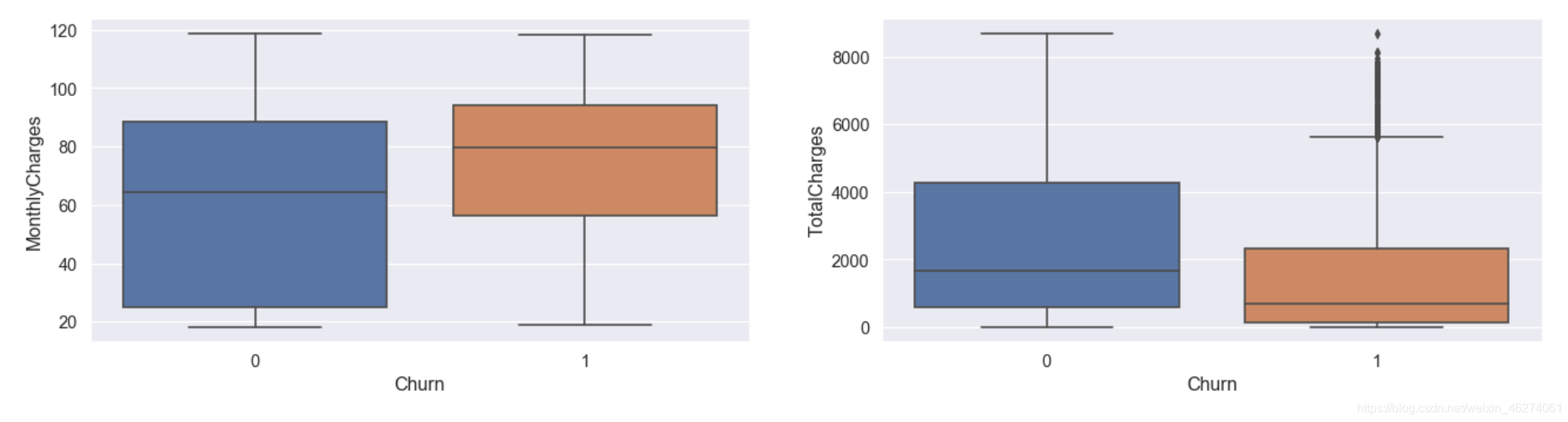
可以看出总消费中，流失用户存在个别异常值，我们可以采取删除，视为缺失值处理，取对数转换，边界值替换等方式处理。

月消费的用户流失数据：

data.groupby("Churn")["MonthlyCharges"].describe().T

总消费的用户流失数据：

data.groupby("Churn")["TotalCharges"].describe().T

小提琴图：

fig=plt.figure(figsize=(20,10),dpi=100)
# 子图1
fig.add_subplot(2,2,1)
sns.violinplot(x="Churn",y="MonthlyCharges",data=data)

# 子图2
fig.add_subplot(2,2,2)
sns.violinplot(x="Churn",y="TotalCharges",data=data)

plt.show()

从以上图中可以看出样本中， 对于月消费来说，月消费高的用户似乎容易流失；对于总消费来说，总消费低的用户似乎容易失去。

差异检验-两样本t检验

以上都是对于样本的结论，那么对于总体来说，是否也符合上述规律呢还是说我们抽样出来的只是凑巧总体并不是这样分布的，那么我们需要差异检验来验证上述结论
我们用两样本t检验，来查看流失用户与未流失用户对于消费来说，他们的均值差异是否显著。

差异检验 --月消费 "MonthlyCharges"
原假设：流失用户的月消费与未流失用户的月消费均值是一致的
总共分位两步
第一步 ：方差齐性检验

churn_1=data[data["Churn"]==1]["MonthlyCharges"]
churn_0=data[data["Churn"]==0]["MonthlyCharges"]
# 进行方差齐性检验-levene检验。 为后续的两样本t检验服务。 方差一致就叫齐性
stats.levene(churn_0,churn_1)

第二步： p值为1.026>=0.05，说明是支持原假设的方差是一致的，equal_var=True
进行两样本t检验-双边检验。方法用的是stats.ttest_ind，注意：两样本的方差相同与不相同，取得的结果是不同的。

r = stats.ttest_ind(churn_0,churn_1,equal_var=True)
print(r)

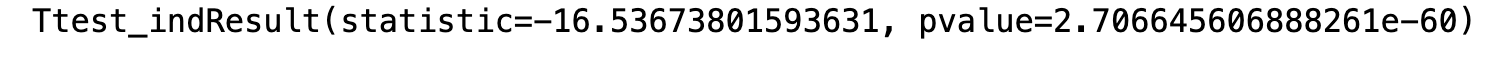p值2.7>=0.05,支持原假设，所以我们还不能认为流失用户的月均消费高于未流失的用户。

同样对于总消费，原假设：总消费均值都是一致的
第一步：方差齐性检验

churn_1=data[data["Churn"]==1]["TotalCharges"]
churn_0=data[data["Churn"]==0]["TotalCharges"]
stats.levene(churn_0,churn_1)

第二步：P值为3.38>0.05，说明是支持原假设的方差是一致的，齐性的，equal_var=True

r = stats.ttest_ind(churn_1,churn_0,equal_var=True)
print(r)

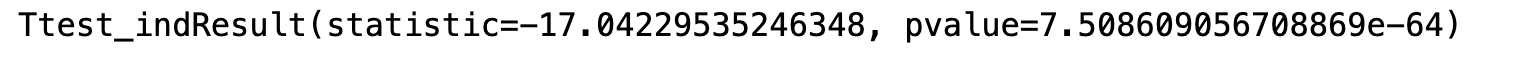
P值7.5>0.05，所以我们也不能认为总体的流失用户的总均消费低于未流失的用户。
下一步，划分消费等级。

分箱离散化

定义消费等级 ，按照各分位数分为低消费 中低消费 中高消费 高消费

def charge_to_level(charge):
    if charge<=da.loc["25%"]:
        return "低消费"
    elif charge<=da.loc["50%"] and charge>da.loc["25%"]:
        return "中低消费"
    elif charge<=da.loc["75%"] and charge>da.loc["50%"]:
        return "中高消费"
    else:
        return "高消费"
da=data["MonthlyCharges"].describe()
data["level_MonthlyCharges"] = data["MonthlyCharges"].apply(charge_to_level)
da=data["TotalCharges"].describe()
data["level_TotalCharges"] = data["TotalCharges"].apply(charge_to_level)


display(data["level_MonthlyCharges"].value_counts())
data.sample(5)

条形图查看：

fig=plt.figure(figsize=(20,10),dpi=80)
# 子图1
fig.add_subplot(2,2,1)
sns.countplot(x="level_MonthlyCharges",hue="Churn",data=data,order=["低消费","中低消费","中高消费","高消费"])

# 子图2
fig.add_subplot(2,2,2)
sns.countplot(x="level_TotalCharges",hue="Churn",data=data,order=["低消费","中低消费","中高消费","高消费"])
plt.show()

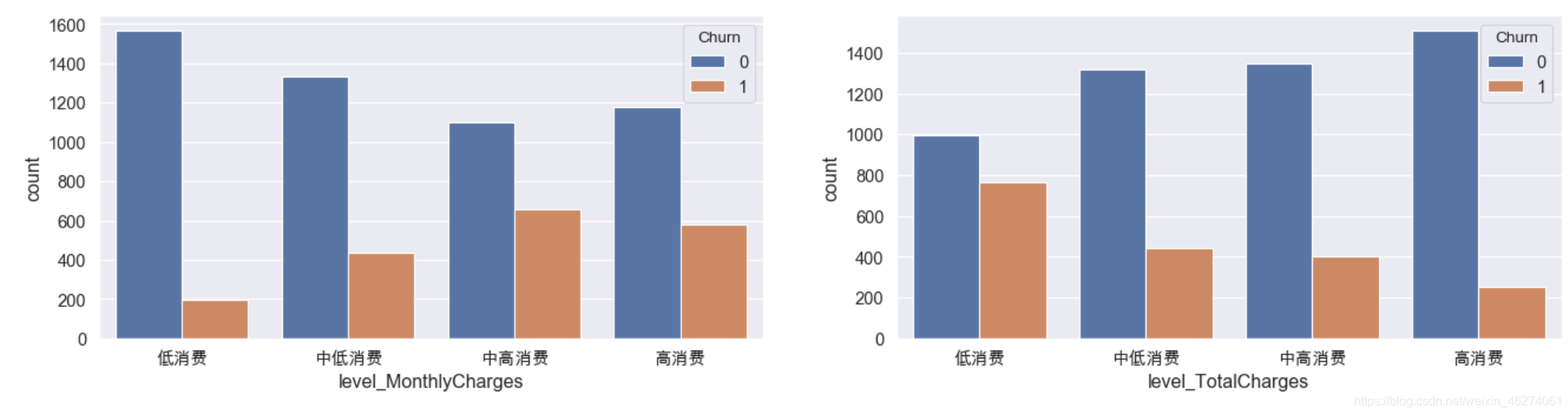
可以看出对于月消费来说，流失用户主要集中在中高消费以及高消费；对于总消费来说，流失用户主要集中在低消费和中低消费中。那么我们可以对这部分用户进行精细化运营以最大程度留住用户。

6.机器学习

基模型的建立

将类别特征离散化处理之前，首先删除不需要离散化处理的特征，作者花了部分时间比较按照分位数分箱离散化和未分箱离散的数据预测得分，发现未分箱的效果好那么一点点，还有个原因是分箱的分界点的选择，如果可以找到最合适的分界点，那么分箱离散化是一个相当不错的选择。这里就只演示未分箱的操作。
删除列MonthlyCharges，TotalCharges，Churn：

y=data["Churn"]
data.drop(['customerID','level_MonthlyCharges','level_TotalCharges',"Churn"],axis=1,inplace=True)
data.head()

使用pandas.get_dummies( )进行one-hot 独热编码，

data_onehot=pd.get_dummies(data)
print(data_onehot.shape)
data_onehot.head()

职业虽然已经是数字，但是在数字中他们有大小的关系，实际职业之间是没有大小比较的，所以也需要进行独热编码。

data_base=pd.get_dummies(data_onehot,columns=['tenure'])
print(data_base.sample(5))
data_base.info()

进行独热编码后占用的内存变少，因为独热编码使用的是稀疏矩阵。

基模型的初始评分

x_train,x_test,y_train,y_test=train_test_split(data_base,y,test_size=0.25,random_state=0)
lr=LogisticRegression()
lr.fit(x_train,y_train)
print("训练集：",lr.score(x_train,y_train))
print("测试集：",lr.score(x_test,y_test))

y_hat = lr.predict(x_test)
# 测试集的混淆矩阵得分值
print(classification_report(y_true=y_test, y_pred=y_hat)) 

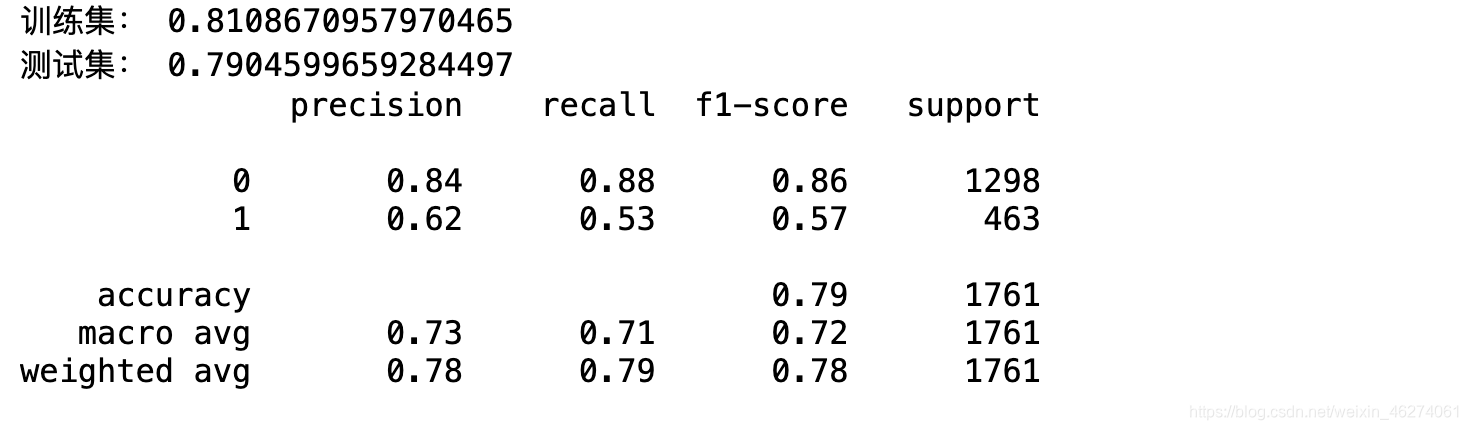
如果只查看正确率accuracy，分值还是蛮高的达到了0.79，但是我们更多关注的是流失用户，所以我们的评估指标选择f1-score调和平均值会更符合气质。
f1分值为0.57。

异常值处理

我们从之前的箱线图可以看出总消费中存在个别的极大值，那么我们现在需要处理一下。

# 从箱线图可以看出只有总消费存在较大的异常值 先计算分位数 IQR
quartile = np.quantile(x_train[y_train==1]['TotalCharges'],[0.25, 0.75])
IQR = quartile[1] - quartile[0]
upper = quartile[1] + 1.5 * IQR
print("IQR:{},upper:{}".format(IQR,upper))
def func(x):
    if x >= upper:
        return upper
    else:
        return x 
x_train.loc[:,'TotalCharges'][y_train==1]= x_train.loc[:,'TotalCharges'][y_train==1].apply(lambda x: func(x))
# x_train['TotalCharges'][y_train==1]= x_train['TotalCharges'][y_train==1].apply(fun)
x_test['TotalCharges'][y_test==1]= x_test['TotalCharges'][y_test==1].apply(lambda x: func(x))

# 查看是否还存在异常值
print(x_train['TotalCharges'][y_train==1][x_train['TotalCharges']>upper])
print(x_test['TotalCharges'][y_test==1][x_test['TotalCharges']>upper])

这里很重要的一点：我们替换异常值应该是从测试集中计算出，而不要把测试集的数据也作为标准来计算出异常值，不然这就毫无意义了。

使用箱线图查看训练集中是否还存在异常值

sns.boxplot(x="Churn",y="TotalCharges",data=pd.concat([x_train,y_train],axis=1))

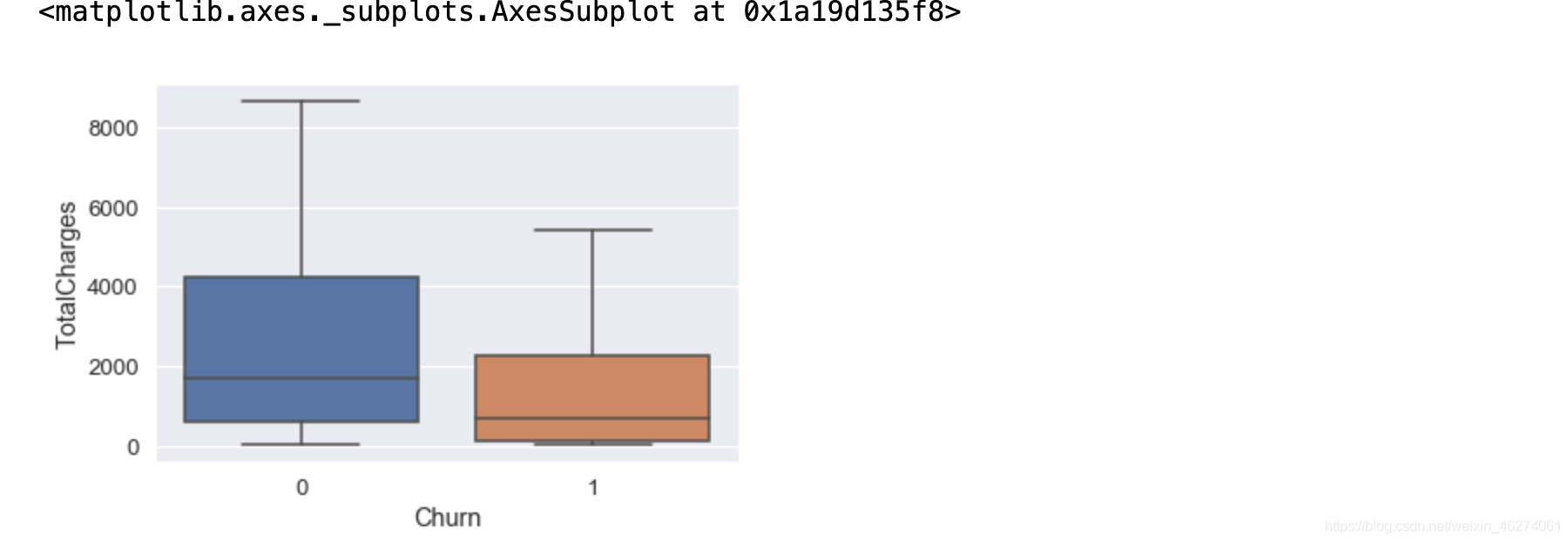
使用箱线图查看测试集中是否还存在异常值

sns.boxplot(x="Churn",y="TotalCharges",data=pd.concat([x_test,y_test],axis=1))

数据标准化处理

虽然逻辑回归中w可以调节由于数据量纲的不同造成的模型不准确，但像KNN这样的模型就会受到量纲在数量级上的不同，从而影响计算距离。所以我们可以先统一进行数据的标准化处理。
数据标准化主要有：均值标准差标准化和最小最大值标准化。
这里两种方式尝试之后 这里采用均值标准差标准化：

from sklearn.preprocessing import StandardScaler, MinMaxScaler
# StandardScaler：均值标准差标准化
# MinMaxScaler：最小最大值标准化
scaler,desc=[StandardScaler()],["均值标准差标准化"]
# scaler,desc=[MinMaxScaler()],["最小最大值标准化"]

for s, d in zip(scaler, desc):
    # fit_transform:将训练集和测试集都进行标准化
    x_train.loc[:,['MonthlyCharges','TotalCharges']] = s.fit_transform(x_train.loc[:,['MonthlyCharges','TotalCharges']])
    x_test.loc[:,['MonthlyCharges','TotalCharges']] = s.transform(x_test.loc[:,['MonthlyCharges','TotalCharges']])
    # 再代入KNN回归算法里
    knn = KNeighborsClassifier(n_neighbors=3, weights="uniform")
    knn.fit(x_train, y_train) 
    y_hat=knn.predict(x_test)
    print(d, knn.score(x_test, y_test))
    print(classification_report(y_true=y_test, y_pred=y_hat))

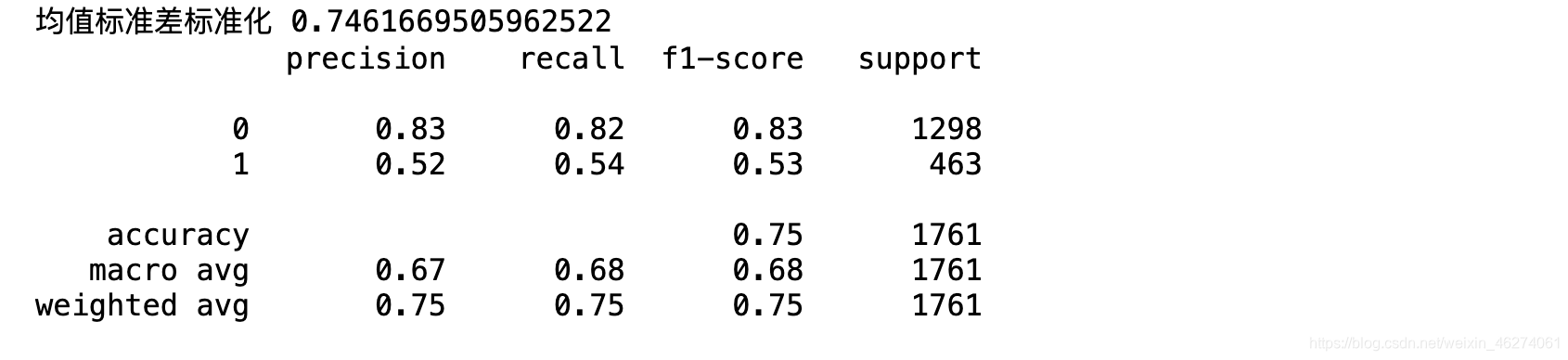
采用逻辑回归查看标准化处理后的评分：

lr = LogisticRegression(multi_class="ovr", solver="liblinear")
lr.fit(x_train,y_train)
print("训练集：",lr.score(x_train,y_train))
print("测试集：",lr.score(x_test,y_test))
y_hat = lr.predict(x_test)
print(classification_report(y_true=y_test, y_pred=y_hat))

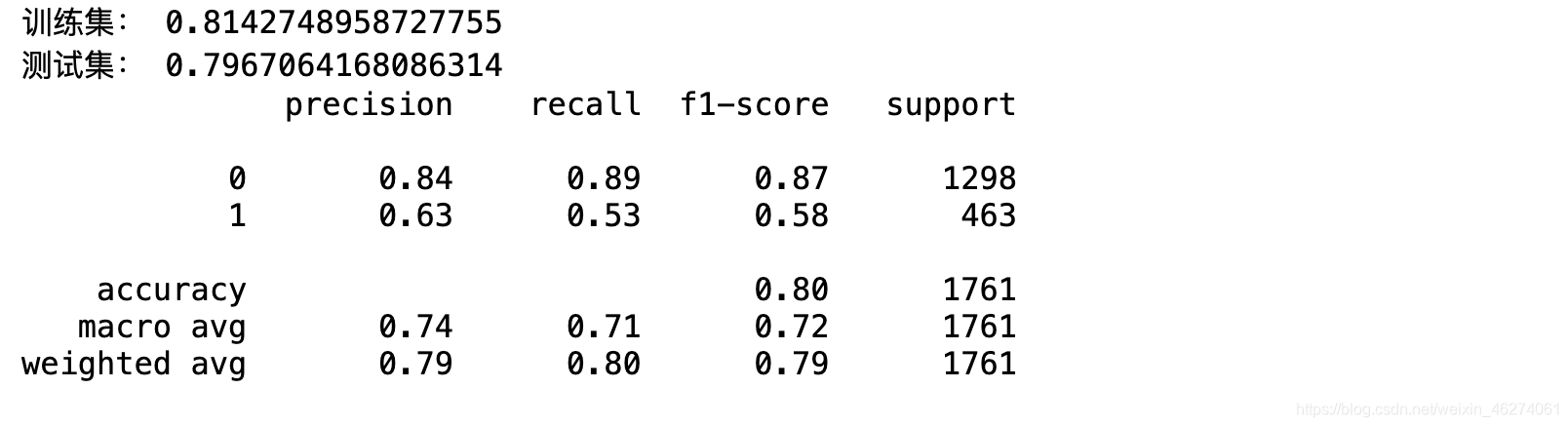
f1调和平均值：0.58

样本不均衡处理&逻辑回归

未处理之前，跑出来的评分模型最高评分有0.60，处理之后有所提升，
处理样本不均衡方法有升采样（上采样），降采样（下采样），升采样的主要方法有SMOTE和ADASYN，降采样不推荐因为样本数量减少对模型是有不良影响的。
这里采用的是上采样，SMOTE和ADASYN对比使用之后，采用SMOTE方法

seed=0
# 邻居数量k测试出来为10有较好的得分
smote=SMOTE(random_state=seed,k_neighbors=10) 
x_resample,y_resample=smote.fit_resample(x_train,y_train)
print(Counter(y_resample))
lr=LogisticRegression()
lr.fit(x_resample,y_resample)
y_hat=lr.predict(x_test)
print(classification_report(y_test,y_hat))
print(f1_score(y_test, y_hat))

升采用之后类别的次数基本相同，达到样本均衡的效果，分值提升到了0.61。

网格交叉验证&KNN

param = {"n_neighbors": range(3,13),
         "weights": ["uniform", "distance"],
        }
gs = GridSearchCV(estimator=KNeighborsClassifier(), param_grid=param,
         cv=2, scoring="f1", n_jobs=-1, verbose=10)
gs.fit(x_resample, y_resample)
print(gs.best_params_)
y_hat = gs.best_estimator_.predict(x_test)
print(classification_report(y_test, y_hat))
# 最好的分值。训练集的分值
print("分值:",gs.best_score_)
# 最好的超参数组合。
print("超参数组合:",gs.best_params_)
# 使用最好的超参数训练好的模型。
print("模型:",gs.best_estimator_)
# {'n_neighbors': 12, 'weights': 'distance'} fi: 0.55

决策树

from sklearn.tree import DecisionTreeClassifier
param = {"criterion": ["gini", "entropy"],
         "max_depth": range(1,10)
         }
gs = GridSearchCV(estimator=DecisionTreeClassifier(), param_grid=param,
         cv=2, scoring="f1", n_jobs=-1, verbose=10)
gs.fit(x_resample, y_resample)
print(gs.best_params_)
y_hat = gs.best_estimator_.predict(x_test)
print(classification_report(y_test, y_hat))
# 最好的分值。
print("分值:",gs.best_score_)
# 最好的超参数组合。
print("超参数组合:",gs.best_params_)
# 使用最好的超参数训练好的模型。
print("模型:",gs.best_estimator_)

流水线&朴素贝叶斯

# 高斯朴素贝叶斯 伯努利朴素贝叶斯 多项式朴素贝叶斯  补充朴素贝叶斯
from sklearn.naive_bayes import GaussianNB, BernoulliNB, MultinomialNB, ComplementNB
from sklearn.pipeline import Pipeline

steps=[("model", None)]
pipe = Pipeline(steps=steps)
# ComplementNB()： 适用于样本不均衡的情况
# param里面的模型也可是决策树，KNN算法，可自行调整
param = {"model": [GaussianNB(), BernoulliNB(), MultinomialNB(), ComplementNB()]}
# 因为是稠密矩阵，因此比较消耗内存空间，内存小的，这里建议改成少的并发数量。
gs = GridSearchCV(estimator=pipe, param_grid=param,
         cv=2, scoring="f1", n_jobs=-1, verbose=10)
gs.fit(x_train, y_train)
print(gs.best_params_)
y_hat = gs.best_estimator_.predict(x_test)
print(classification_report(y_test, y_hat))

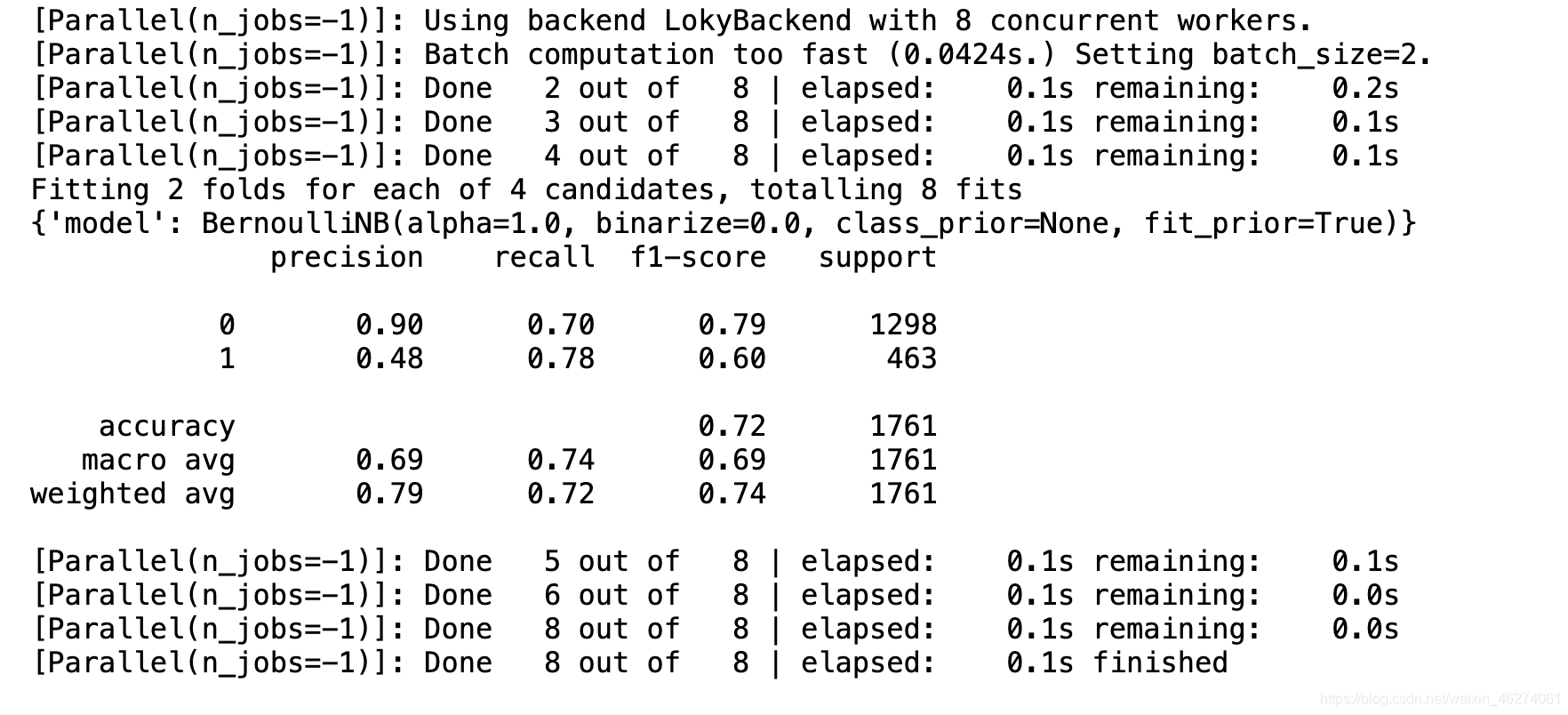
多层感知器

神经网络当中存在隐藏层
当神经网络只有一层就是我们的逻辑回归

from sklearn.neural_network import MLPClassifier
# 这儿只画了两个隐藏层，第一个隐藏层5个神经元，第二个隐藏层4个神经元
# for i in range(1,5):
#     for j in range(5,7):
param = {"hidden_layer_sizes": [(5,), (4,)],
        }
gs = GridSearchCV(estimator=MLPClassifier(), param_grid=param,
        cv=2, scoring="f1", n_jobs=-1, verbose=10)
gs.fit(x_resample, y_resample)
print(gs.best_params_)
y_hat = gs.best_estimator_.predict(x_test)
print(classification_report(y_test, y_hat))
f1=f1_score(y_test, y_hat)

模型得分总结

在经过了数据标准化，样本不均衡处理之后，带入多种模型中，虽然accuracy得分都差不多能达到0.8，但是我们的关注点在于流失用户，所以评估指标采用f1，最后决策树的得分最高为0.63，比初始0.57分有所提升。