案例：AQI分析与预测
本博客主要来自作者对开课吧老师梁勇老师的学习笔记，想深入学习的同学就去开课吧报名吧。
1. 研究背景
AQI（空气质量指数），用来衡量空气清洁或者污染的程度。值越小，表示空气质量越好。近年来，因为环境问题，空气质量也越来越受到人们的重视。
2. 提出问题
哪些城市的空气质量较好？
空气质量在地理位置上是否具有一定的规律性？
临海城市的空气质量是否有别于内陆城市？
空气质量主要受哪些因素影响？
全国城市空气质量普遍处于何种水平？
怎样预测一个城市的空气质量？
3. 数据集描述
此数据集有12个变量，326条数据。
| City | 城市名 |
| AQI | 空气质量指数 |
| Precipitation | 降雨量 |
| GDP | 城市生产总值 |
| Temperature | 温度 |
| Longitude | 经度 |
| Latitude | 纬度 |
| Altitude | 海拔高度 |
| PopulationDensity | 人口密度 |
| Coastal | 是否沿海 |
| GreenCoverageRate | 绿化覆盖率 |
| Incineration(10,000ton) | 焚烧量（10000吨） |
4. 分析流程
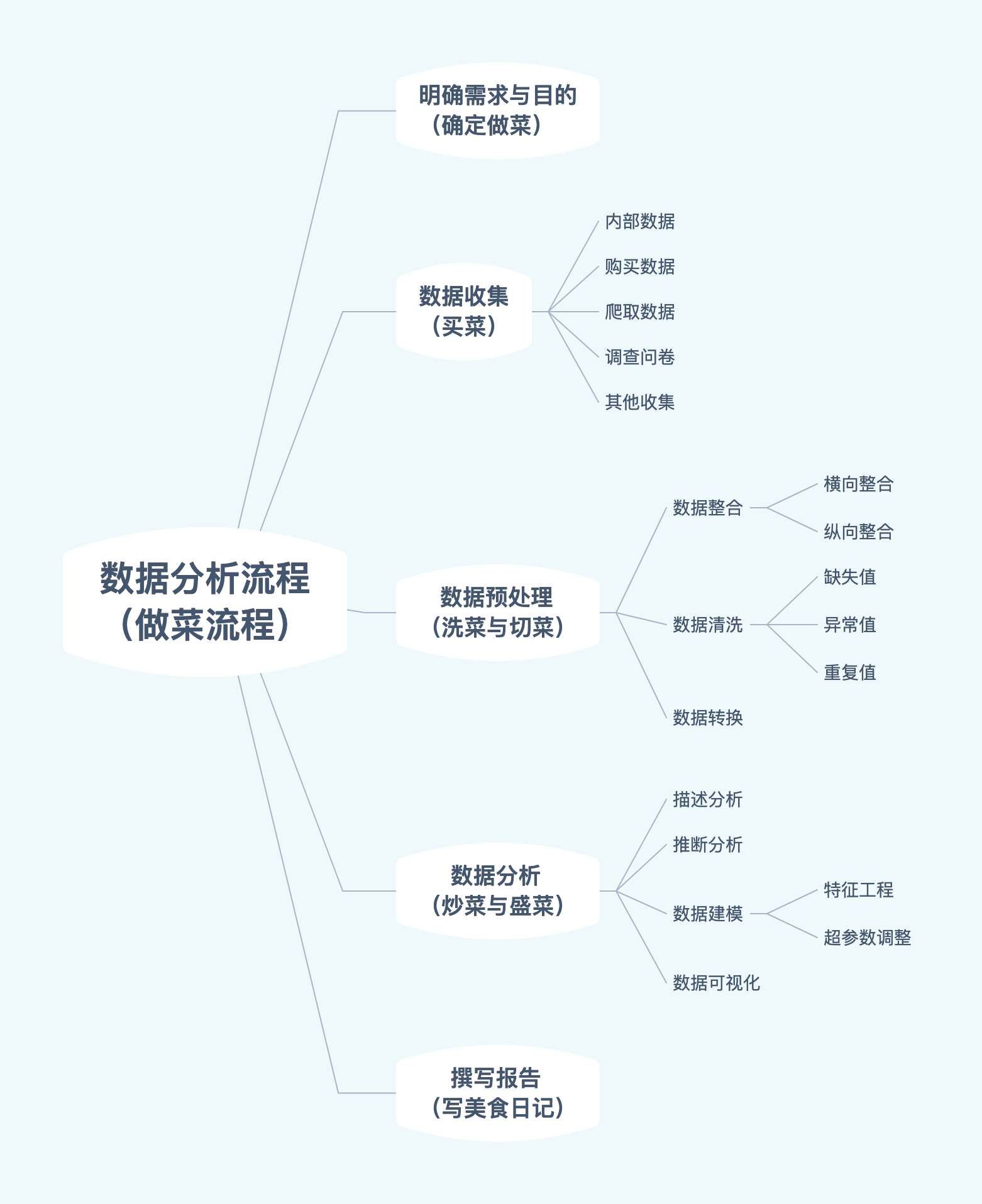
难点理解
特征工程：最大限度地从原始数据中提取特征以供算法和模型使用。通俗的说就是数据预处理的方式，从源数据当中提取相关数据可以放到模型当中
超参数调整：模型参数通常是有数据来驱动调整。超参数不需要数据来驱动，而是在训练前或者训练中人为的进行调整的参数
5.数据预处理
5.1 导入相关库
数据处理
import numpy as np import pandas as pd
可视化
import matplotlib.pyplot as plt import seaborn as sns # 设置风格 --网格颜色风格 sns.set(style="darkgrid") # windows 设置字体为SimHei显示中文 # plt.rcParams["font.family"]="SimHei" # mac plt.rcParams['font.family'] = ['Arial Unicode MS'] # 设置正常显示字符 plt.rcParams['axes.unicode_minus'] = False
特征工程
from sklearn.model_selection import train_test_split #特征切分 切分训练集与测试集 from sklearn.feature_selection import RFECV #RFECV方法 from sklearn.preprocessing import KBinsDiscretizer #分箱操作
算法
from sklearn.linear_model import LinearRegression #线性回归算法
警告忽略
import warnings warnings.filterwarnings('ignore')
5.2 加载数据集
data = pd.read_csv("data.csv") data.shape
查看数据大致情况
# data.head() # data.tail() data.sample(10)
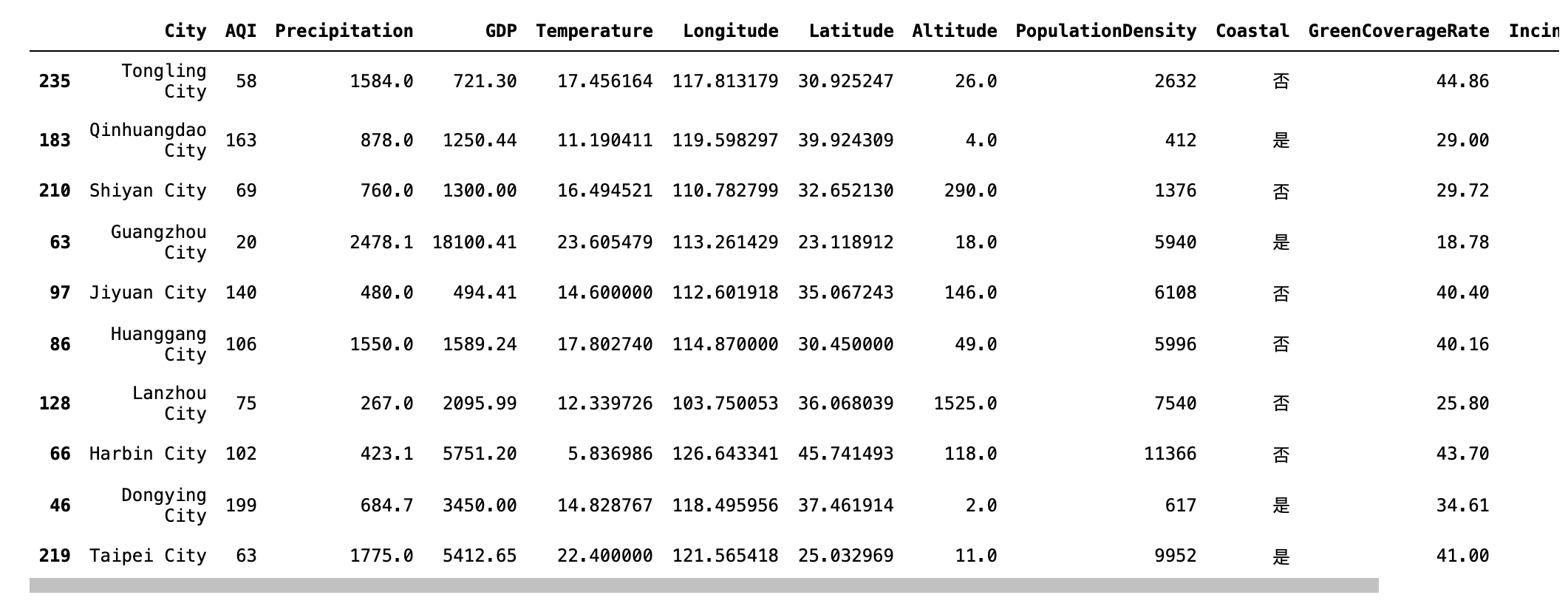
5.3 数据探索(EDA)
5.3.1缺失值探索
# 查看缺失值 # data.info() # 默认为0轴 data.isnull().sum(axis=0)
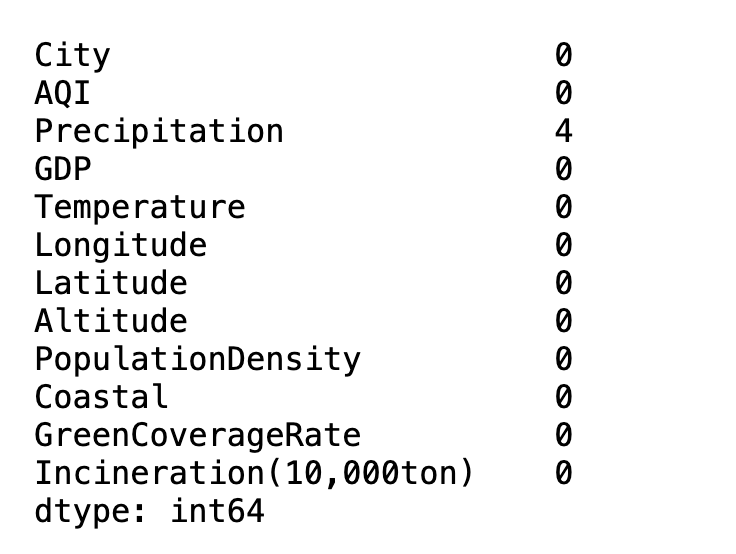
缺失值处理方案
删除缺失值：仅当缺失数量很少的情况下
填充缺失值：
数值变量：
均值：如果是正态分布用均值填充也可以，但是如果是右偏分布就不可以用均值填充了，因为会受到极值的影响
中位数: 中位数不太受异常值或者极值的影响。
类别变量：众数填充，或者单独作为一个类别
额外处理说明：
缺失值小于20%，直接填充
缺失值在20%-80%，填充变量后，新增一列标记该列是否缺失，参与后续建模
缺失值大于80%，不用原始列，新增一列说明该列是否缺失，参与后续建模
# 查看数据分布 偏度 查看左偏还是右偏查看左偏还是右偏 print(data["Precipitation"].skew()) # 查看删除缺失值之后的图形 右偏 seaborn不支持空值绘制图形，所以需要使用dropna()将空值剔除掉 sns.distplot(data["Precipitation"].dropna())
填充数据 中位数填充缺失值
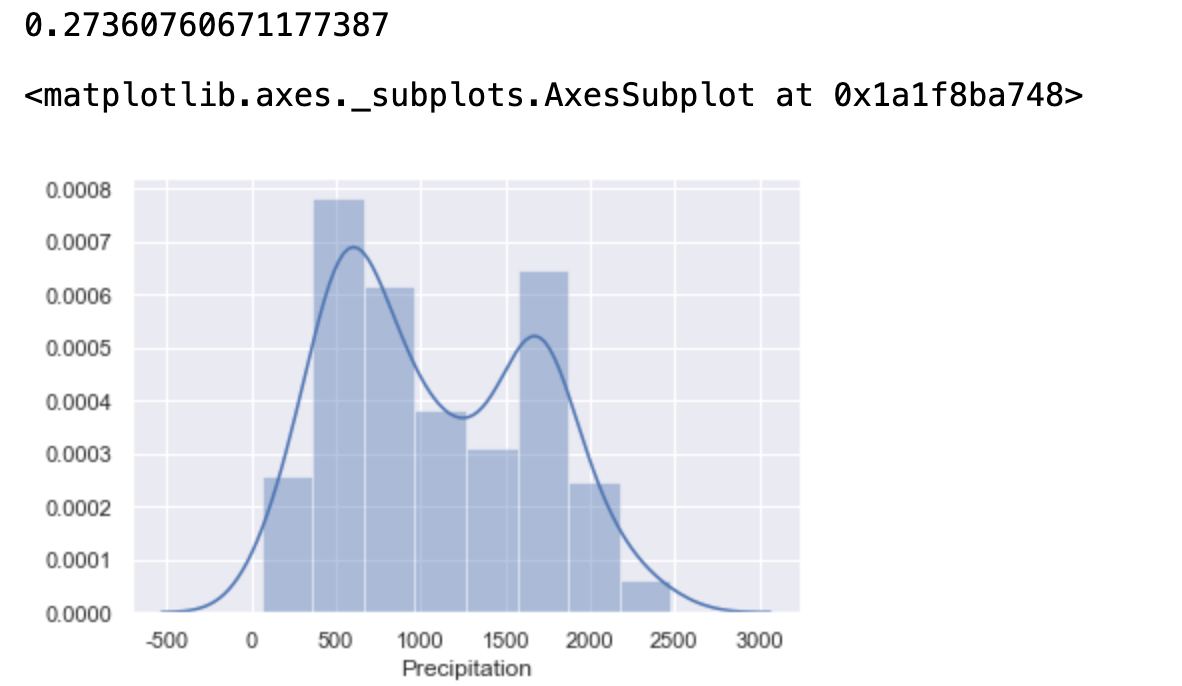
data = data.fillna({"Precipitation" : data["Precipitation"].median()})
data.isnull().sum(axis=0)
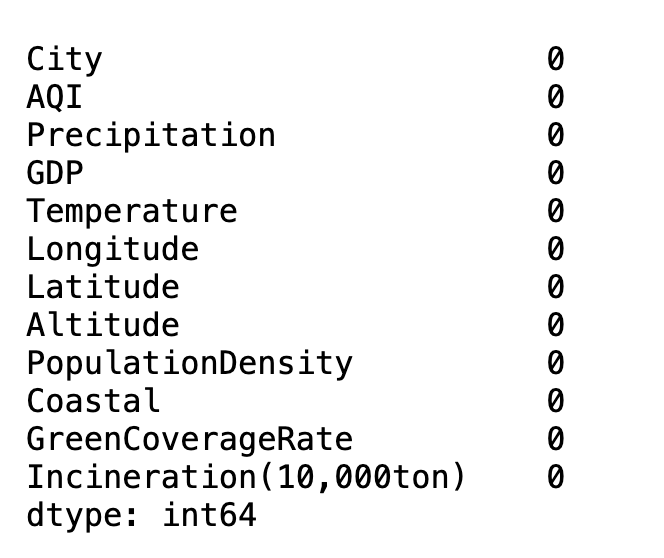
5.3.2 异常值处理
查看数据信息
# describe查看数据信息 data.describe()
3σ 将3σ之外的值视为异常值
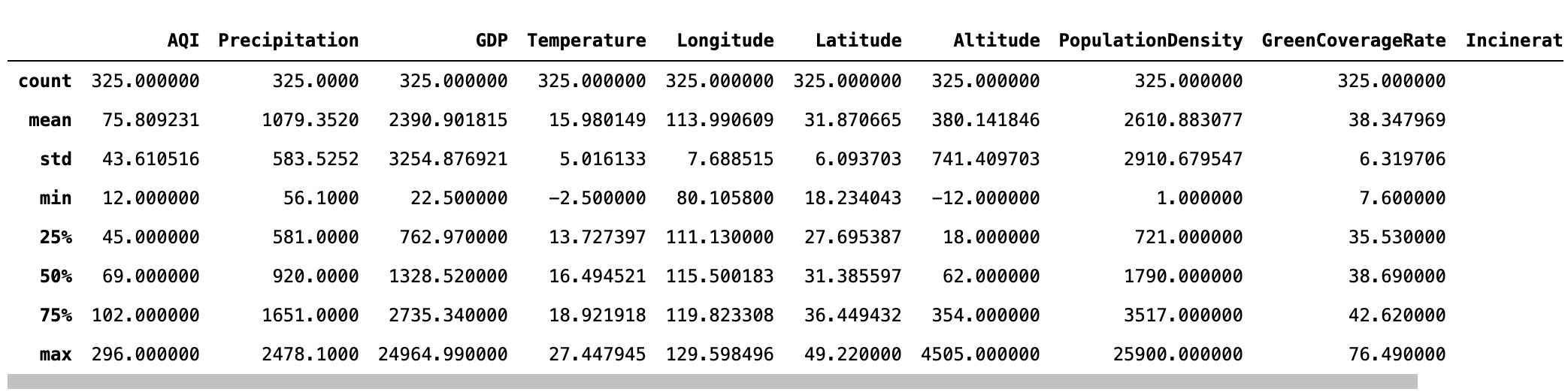
# 作图 sns.distplot(data["GDP"]) # 偏度 print(data["GDP"].skew())
呈现严重右偏 获取异常值
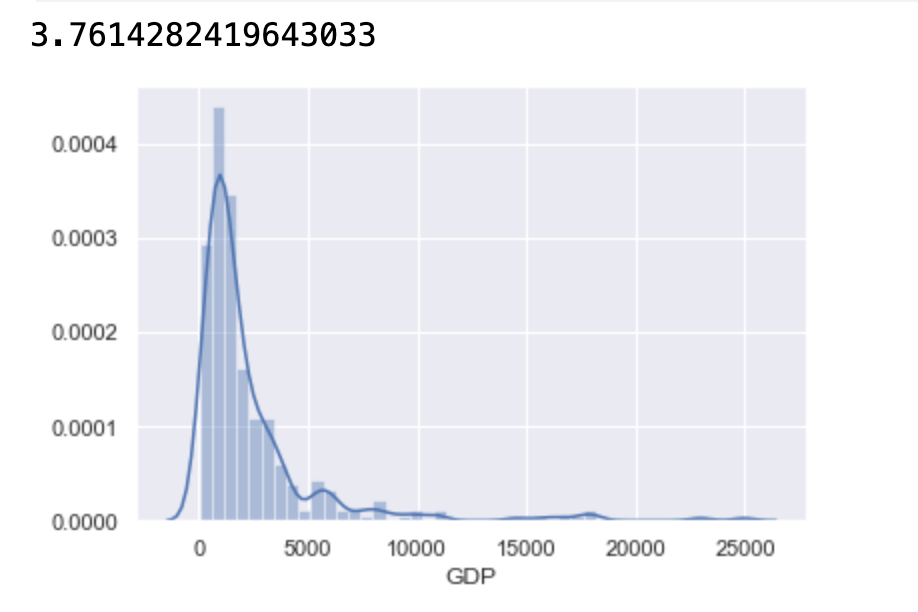
mean,std = data["GDP"].mean(),data["GDP"].std() lower,upper = mean-3*std,mean+3*std print("均值：",mean) print("标准差：",std) print("下限：",lower) print("上限：",upper) data["GDP"][(data["GDP"]<lower) | (data["GDP"]>upper)]
箱线图
--常见的异常检测方式
可以看出合理范围内的最大值最小值，Q1,Q2,Q3为四分位中的四分之一，二，三分位。
四分位距：IQR=Q3-Q1 其实就是箱子的高度
异常值：<Q1-1.5IQR 或者 >Q3+1.5IQR
箱线图合理范围的最大值：Q3+1.5IQR
最小值：Q1-1.5IQR
但是也不是绝对的，因为数据集中的最大值最小值范围有可能小于箱线图算出来的最大值最小值范围
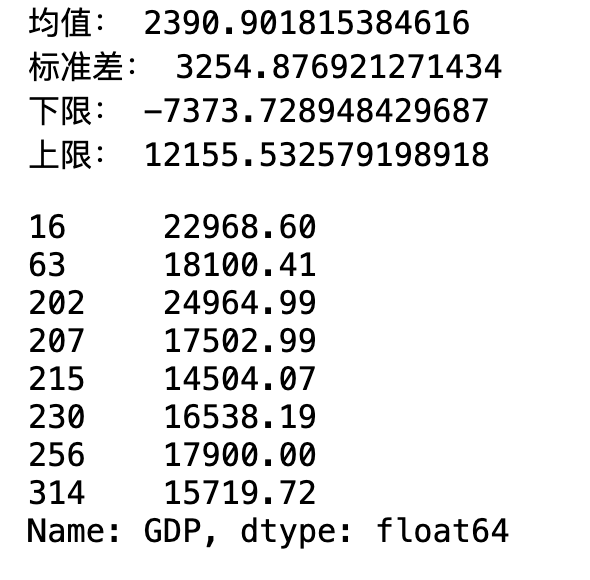
sns.boxplot(data=data["GDP"])
异常值处理
# 1.删除异常值
2.视为缺失值处理
3.对数转换 --现实数据一般情况要么正态分布，要么右偏
下一步可进行建模预测，不可再用于描述性分析，如：求和
取对数适用于正数，如果有其他值 我们可如下对数转换：
np.sign(X)*np.log(np.abs(X)+1)
np.sign(X):大于0的返回1 # sign(2) = 1
小于0的返回-1 # sign(-3) = -1
等于0的返回0 # sign(0) = 0
log(np.abs(X)+1):表示以e为底，np.abs(X)+1的对数
4.使用边界值替代：在3设个么和箱线图中就是这样处理
5.分箱离散化：特征对目标值的影响不是线性的，而是一段一段的对结果有影响，适用于阶梯型的数据，如：年龄对于胳膊长度，维度对于温度
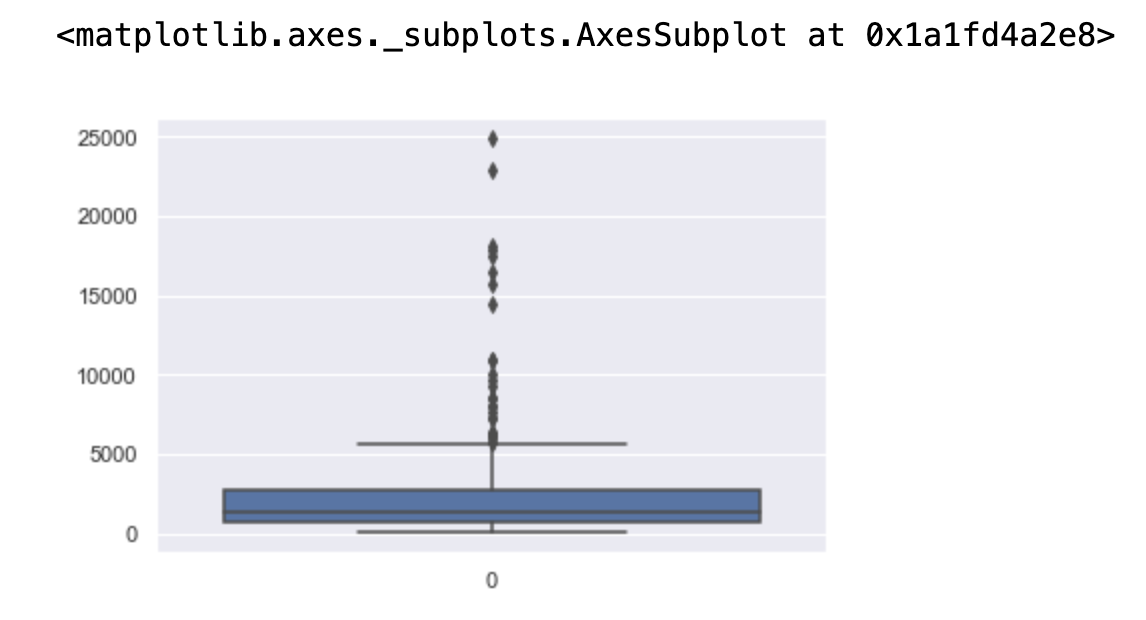
对数转换 （# 边界值处理 ，# 分箱离散化处理）
# 如果存在较大异常值 这样可以得到一定缓解 例如：GDP fig, ax = plt.subplots(1,2) fig.set_size_inches(15,5) sns.distplot(data["GDP"],ax=ax[0]) sns.distplot(np.log(data["GDP"]),ax=ax[1])
5.3.3 重复值处理
发现重复值
# 重复值处理 # 发现重复值 print(data.duplicated().sum()) # 查看哪些记录出现了重复值 # keep='first'/'last'/False 只显示第一次出现、最后一次出现，全部显示 data[data.duplicated(keep=False)]
duplicated( )函数：df.duplicated(subset=None, keep=‘first’/‘last’/False)
subset：对应值是列名,表示只考虑写的列,将列对应值相同的行进行去重，默认值None,即考虑所有列；
keep='first/last/False’：first：默认值，除了第一次出现外，其余相同的被标记为重复；
last：除了最后一次出现外，其余相同的被标记为重复；
False：即所有相同的都被标记为重复；
使用duplicated()函数检测标记Series中的值、DataFrame中的记录行是否是重复，重复为True，不重复为False。
直接删除重复值
data.drop_duplicates(inplace=True)
data.duplicated().sum()
结果为：0
6. 数据分析
6.1 空气质量最好/最差的5个城市
空气质量最好的5个城市
t = data[["City","AQI"]].sort_values("AQI") tt = t.iloc[:5] display(tt) # 条形图:sns.barplot() plt.xticks(rotation=45) sns.barplot(x="City",y="AQI",data=tt) # sns.barplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, estimator=np.mean, ci=95, n_boot=1000, units=None, orient=None, color=None, palette=None, saturation=.75, errcolor=".26", errwidth=None, capsize=None, dodge=True, ax=None, **kwargs) # matplotlib画图 条形图 # plt.bar(x="City",height= "AQI",data=tt,color=['r','g','b','r','g','b'])
空气质量最差的5个城市
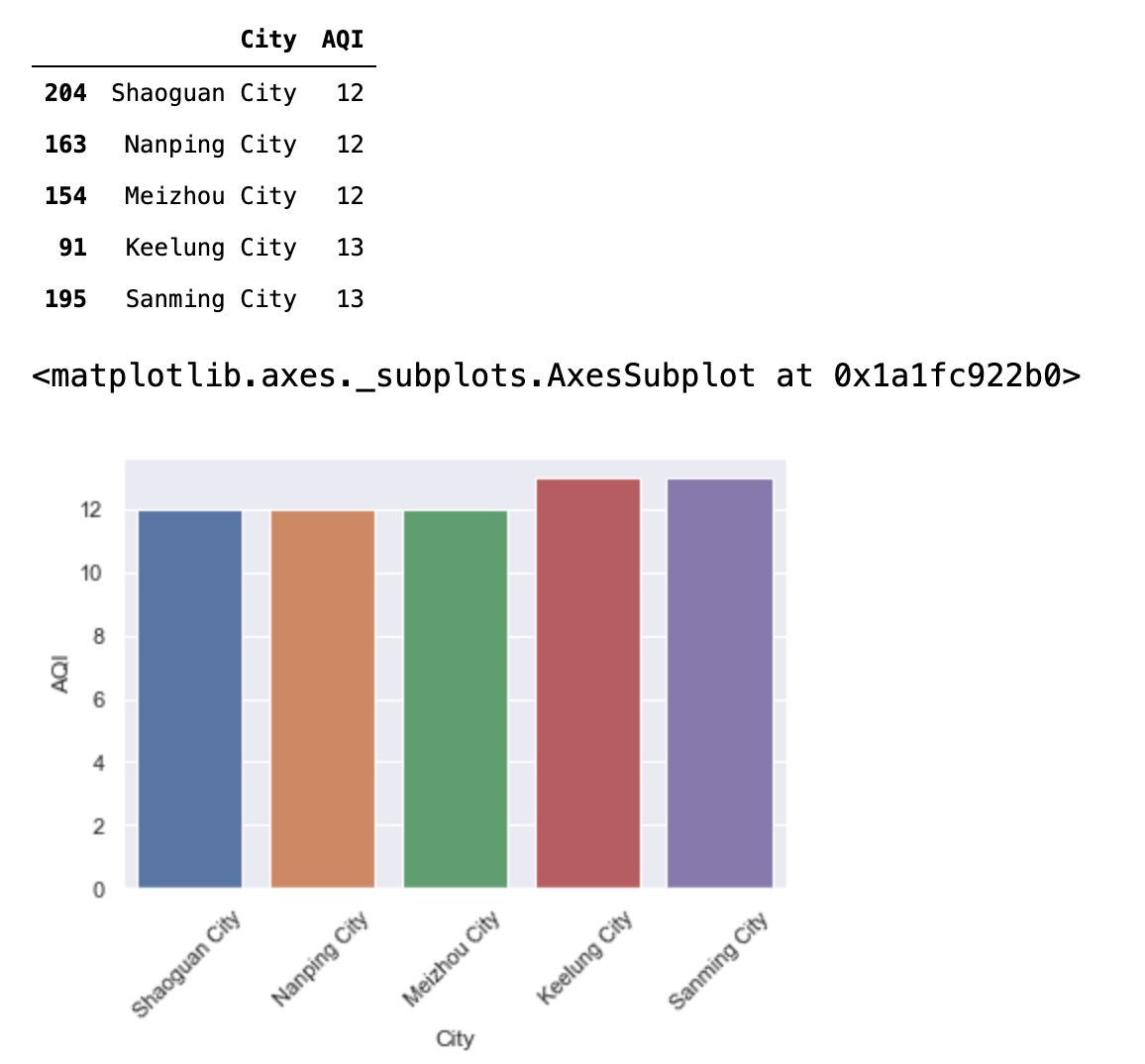
tt = t.iloc[-5:] display(tt) plt.xticks(rotation=45) sns.barplot(x="City",y="AQI",data=tt)
6.2 全国空气的空气质量
城市空气质量等统计
# 统计每个等级的数量 def value_to_level(AQI): if AQI >= 0 and AQI <= 50: return "一级" elif AQI >= 51 and AQI <= 100: return "二级" elif AQI >= 101 and AQI <= 150: return "三级" elif AQI >= 151 and AQI <= 200: return "四级" elif AQI >= 201 and AQI <= 300: return "五级" else: return "六级" level = data["AQI"].apply(value_to_level) display(level.value_counts()) # sns.countplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, orient=None, color=None, palette=None, saturation=.75, dodge=True, ax=None, **kwargs) sns.countplot(x=level,order=["一级","二级","三级","四级","五级","六级"])
散点图:
sns.scatterplot()
# 空气质量指数分布图 # x,y经纬度 # hue="AQI":根据AQI来划分颜色等级 # palette=plt.cm.RdYlGn_r：选的调色板 sns.scatterplot(x="Longitude",y="Latitude",hue="AQI",palette=plt.cm.RdYlGn_r,data=data) # sns.scatterplot(x=None, y=None, hue=None, style=None, size=None, data=None, palette=None, hue_order=None, hue_norm=None, sizes=None, size_order=None, size_norm=None, markers=True, style_order=None, x_bins=None, y_bins=None, units=None, estimator=None, ci=95, n_boot=1000, alpha="auto", x_jitter=None, y_jitter=None, legend="brief", ax=None, **kwargs)
可以看出：南方比北方好，西方比东方好。
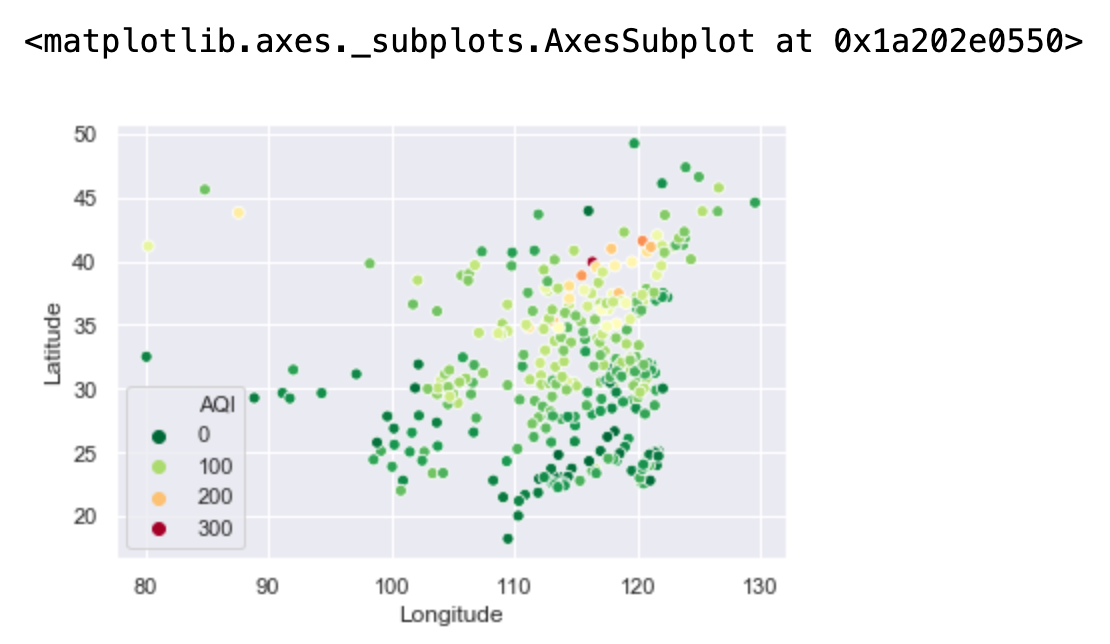
6.3 临海城市的空气质量是否优于内陆
数量统计: 统计沿海城市与内陆城市的数量
display(data["Coastal"].value_counts()) sns.countplot(x="Coastal",data=data)
分布统计 沿海城市与内陆城市的散点分布
条形的散点图：sns.stripplot()
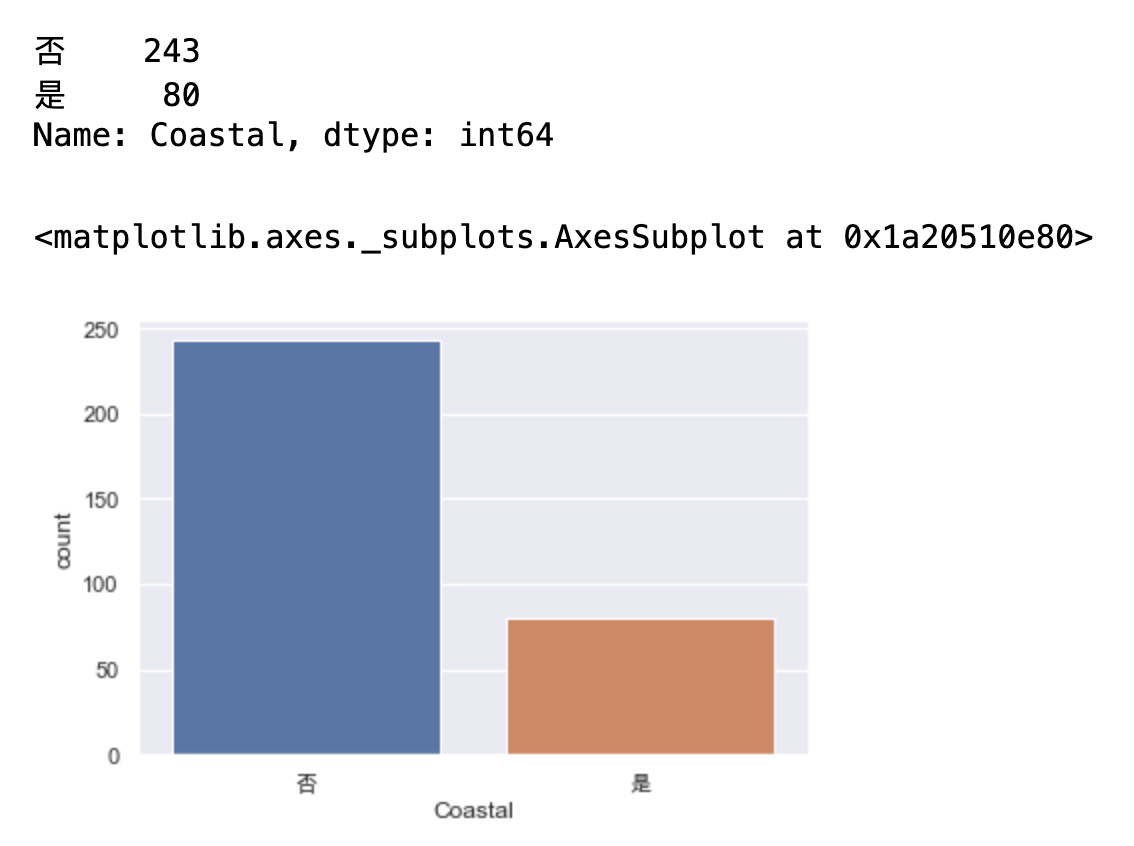
sns.stripplot(x="Coastal",y="AQI",data=data) # sns.stripplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, jitter=True, dodge=False, orient=None, color=None, palette=None, size=5, edgecolor="gray", linewidth=0, ax=None, **kwargs)
蜂群图 :sns.swarmplot()
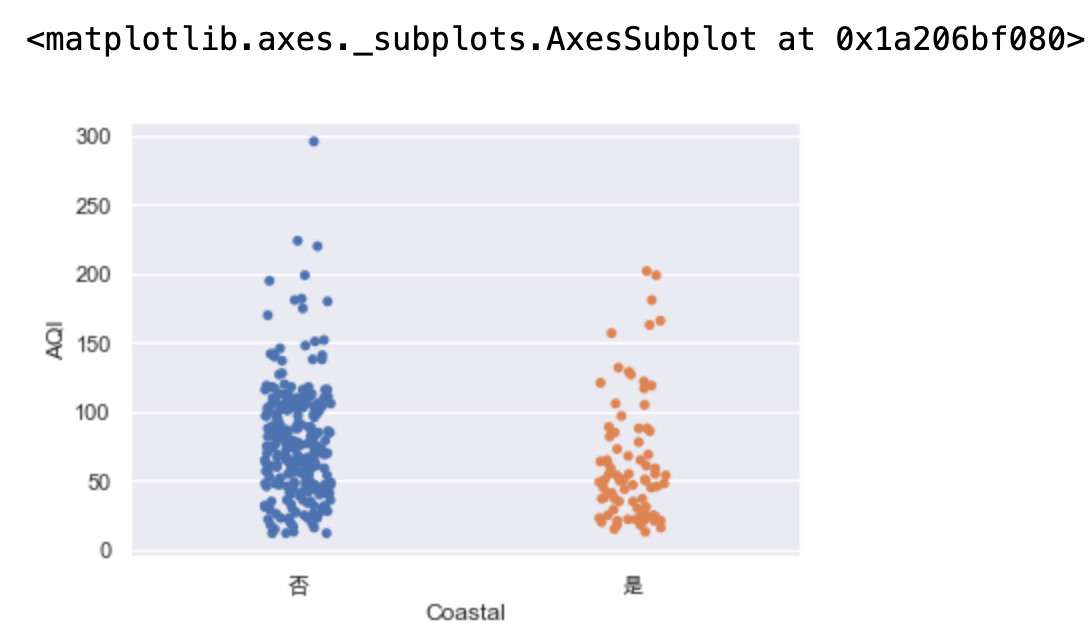
sns.swarmplot(x="Coastal",y="AQI",data=data) # sns.swarmplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, dodge=False, orient=None, color=None, palette=None, size=5, edgecolor="gray", linewidth=0, ax=None, **kwargs)
分组计算空气质量的均值
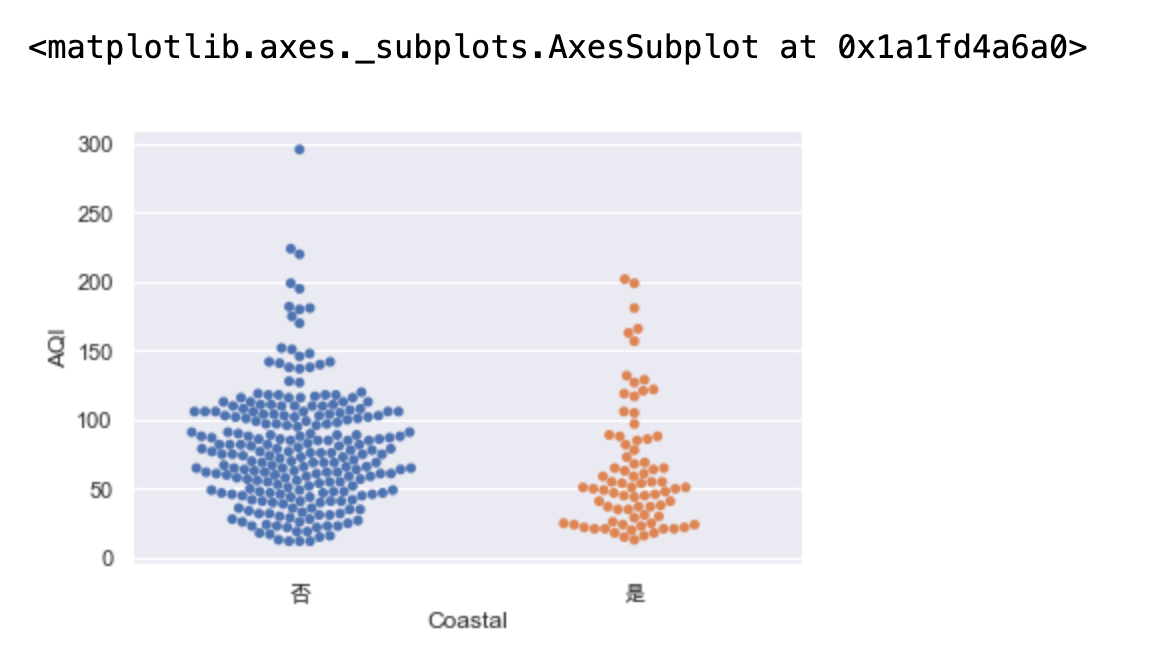
display(data.groupby("Coastal")["AQI"].mean()) # barplot内部会自己求均值 sns.barplot(x="Coastal",y="AQI",data=data) # 图中那条线代表总体均值所在的置信区间 默认为95%的置信度
箱线图 :sns.boxplot()
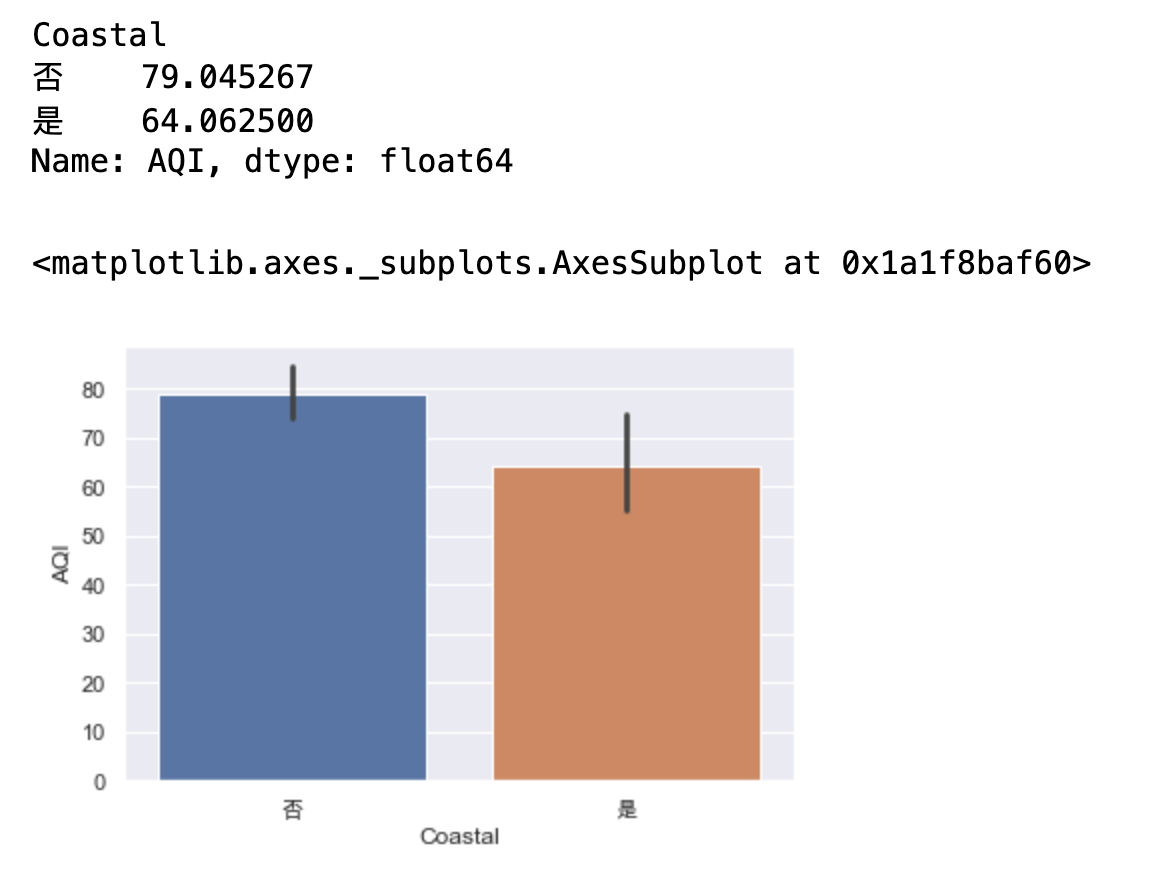
# 可以查看更多信息 四分位 最大值最小值 异常值 sns.boxplot(x="Coastal",y="AQI",data=data) # sns.barplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, estimator=np.mean, ci=95, n_boot=1000, units=None, orient=None, color=None, palette=None, saturation=.75, errcolor=".26", errwidth=None, capsize=None, dodge=True, ax=None, **kwargs)
小提琴图 sns.violinplot()
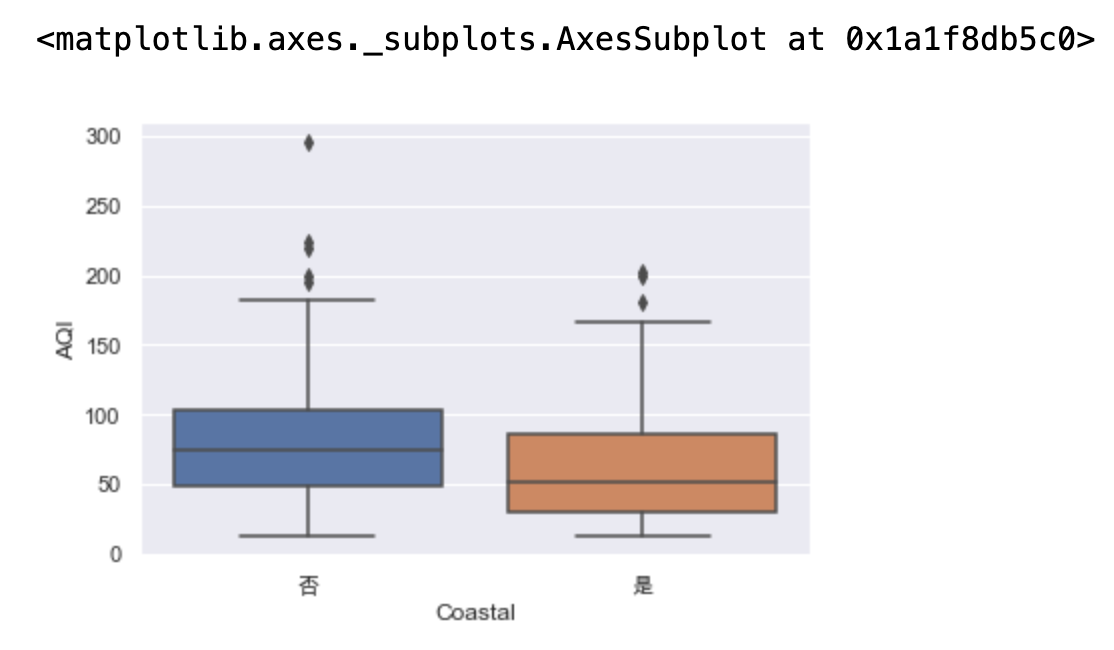
# 还能展现分布的密度 # 里面的是微型版的箱线图，外边是核密度图kde，小提琴图向右旋转90度，就可以看出这是个右偏的 sns.violinplot(x="Coastal",y="AQI",data=data) # sns.violinplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, bw="scott", cut=2, scale="area", scale_hue=True, gridsize=100, width=.8, inner="box", split=False, dodge=True, orient=None, linewidth=None, color=None, palette=None, saturation=.75, ax=None, **kwargs)
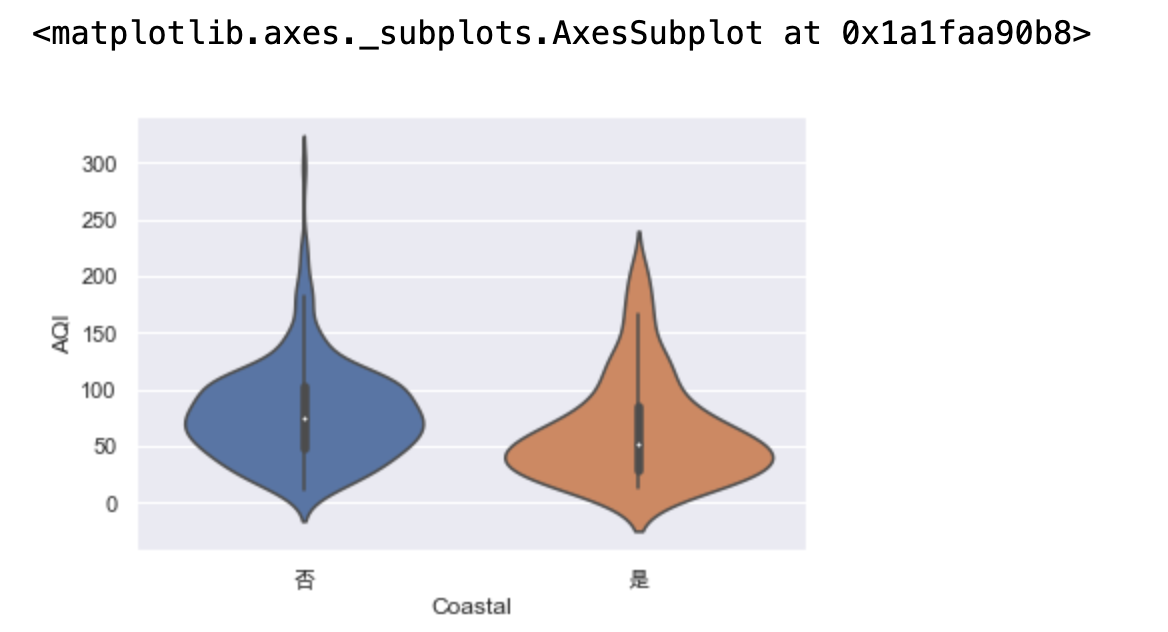
混合图形
# 散点图(这里用的蜂群图)与箱线图或小提琴图结合在一起进行绘制 一般不作为分析的主要手段 # inner=None:不展示里面的琴弦 sns.violinplot(x="Coastal",y="AQI",data=data,inner=None) sns.swarmplot(x="Coastal",y="AQI",color="g",data=data) # sns.boxplot(x="Coastal",y="AQI",color="g",data=data)
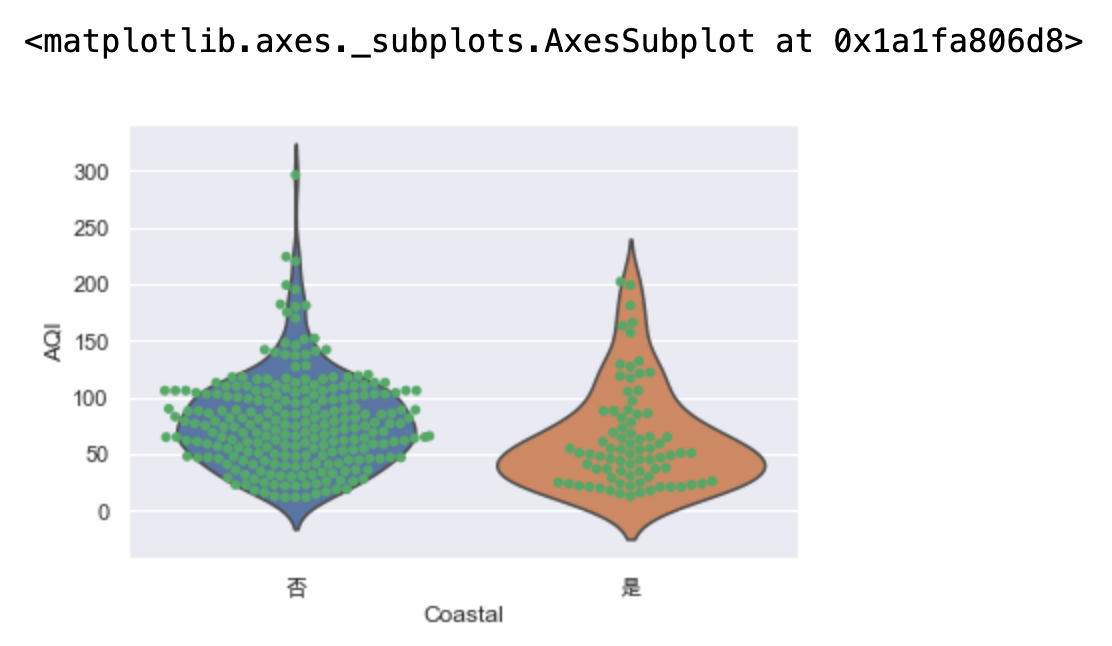
收集到的样本不能说明总体上的差异性，因为抽样可能会带来一定的误差
6.4 空气质量主要受哪些因素影响
假设检验
-差异检验
两独立样本t检验： 查看临海城市与内陆城市的背后总体的均值差异是否显著
（扩展--两相关样本t检验：也叫配对样本t检验，经过某一个相关的改善前改善后，或者同一个人经受两个相关的仪器得出来的反应，比如同一个人接触猫，狗的反应时间）
# 原假设：均值一致
# 备择假设：均值不一致
先查看方差是否齐性
方差齐性检验：查看两独立样本的方差是否一致
# 差异检验 # 两样本t检验 查看临海城市与内陆城市的均值差异是否显著 # 原假设：均值一致 # 备择假设：均值不一致 from scipy import stats coastal = data[data["Coastal"] == "是"]["AQI"] inland = data[data["Coastal"] == "否"]["AQI"] # 进行方差齐性检验-levene检验。 为后续的两样本t检验服务。 方差一致就叫齐性
# levene检验比较稳定
stats.levene(coastal,inland) # 如果P值大于0.05，那么我们认为两总体具有方差齐性 # p值为76%，有76%支持原假设 方差是齐性的，所以下面的equal_var=True。
引出如下：方差一致计算方法
# 进行两样本t检验。方法用的是stats.ttest_ind，注意：两样本的方差相同与不相同，取得的结果是不同的。
# 如果两总体不具有方差齐性，参数修改：equal_var=False
r = stats.ttest_ind(coastal,inland,equal_var=True) print(r) # 双边检验结果中p值非常小 说明不支持原假设两样本不一致, statistic<0,说明coastal<inland,
# 所以下面用右边假设检验 即沿海城市的AQI小于内陆
p = stats.t.sf(r.statistic,df=len(coastal)+len(inland)-2) print(p) # p值非常大，支持原假设 沿海小于内陆
空气质量主要受哪些影响？
散点图矩阵：sns.pairplot()
作用：可以大致查看两两变量之间的关系 这里并不是很明显 画图是一种辅助 有主观色彩 不能当做一种标准
代码及示意图如下：
# 散点图矩阵 ：sns.pairplot() # --可以大致查看两两变量之间的关系 这里并不是很明显 画图是一种辅助 有主观色彩 不能当做一种标准 # 对角线是直方图绘制：同一个变量展现的是在一个小区间内有多少个值 sns.pairplot(data[["AQI", "PopulationDensity", "GreenCoverageRate"]]) # sns.pairplot(data[["AQI", "PopulationDensity", "GreenCoverageRate"]], kind="reg") # kind默认情况下是scatter，reg是画一条回归线
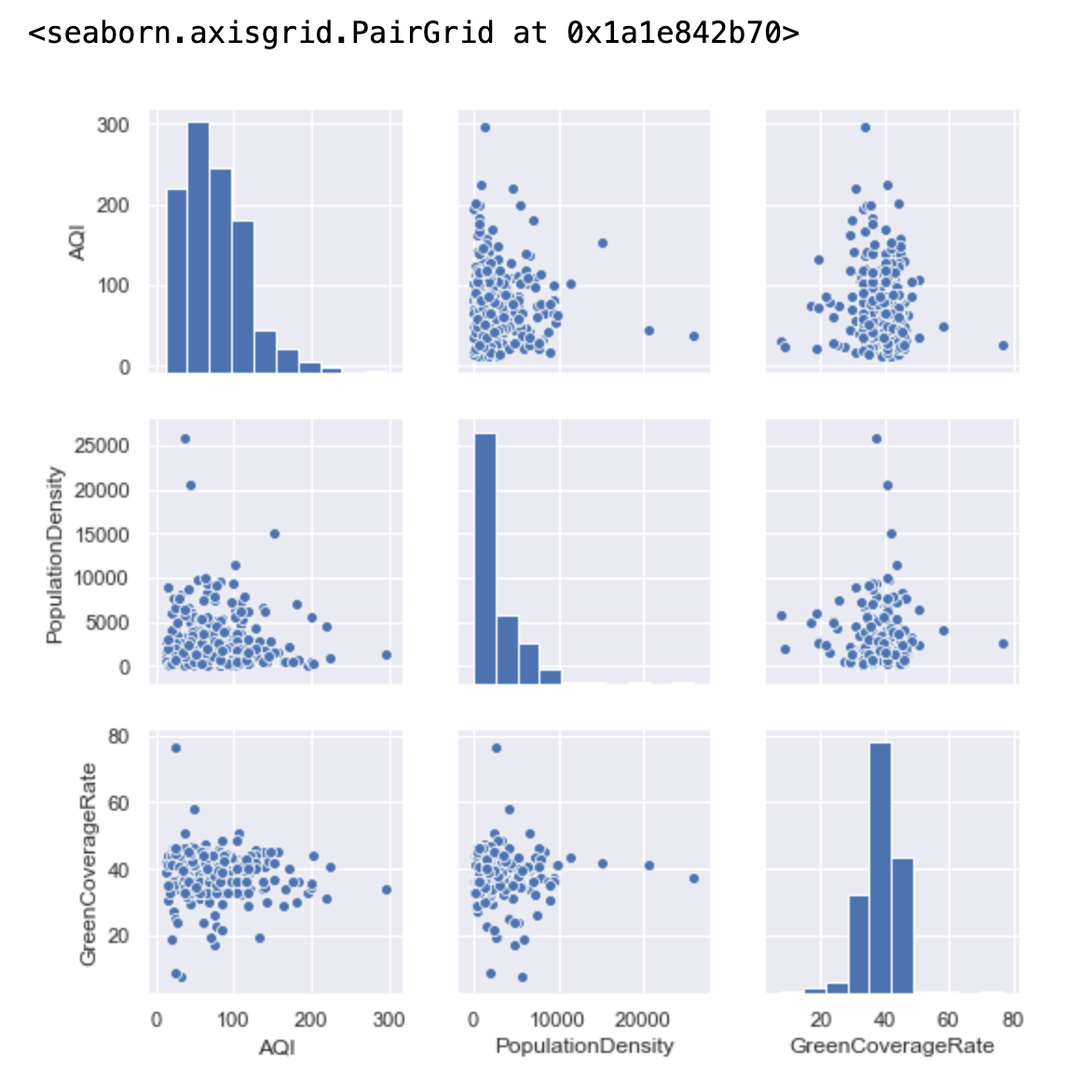
如何量化：采用相关系数
先看下协方差：
协方差：协方差体现的是两个变量之间的分散性以及两个变量变化步调是否一致。容易得知，当协方差的两个变量相同时，协方差就是方差。
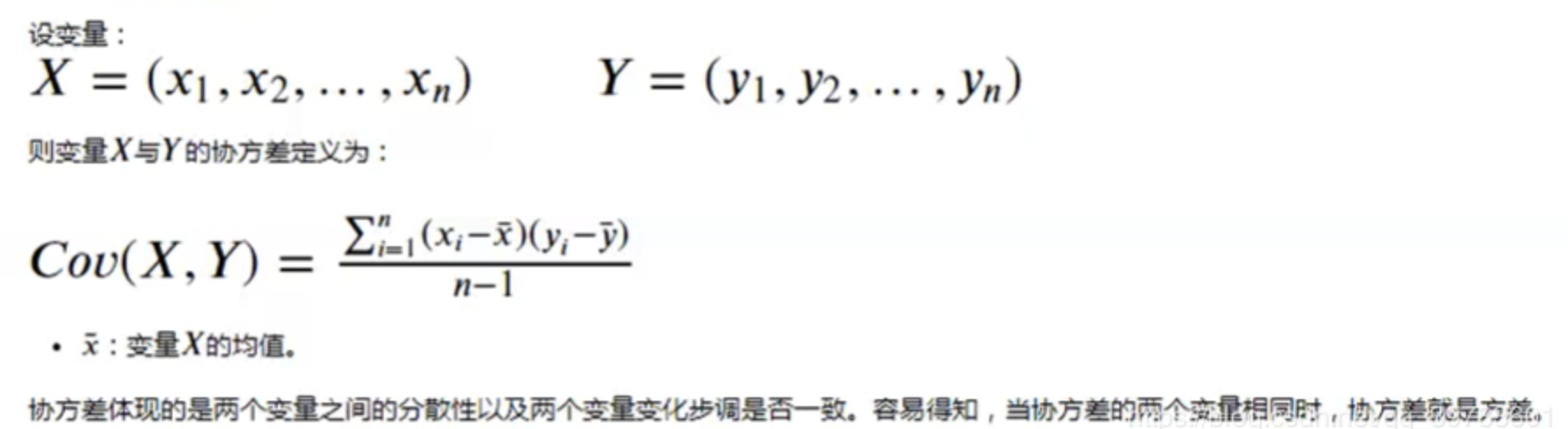
相关系数公式：
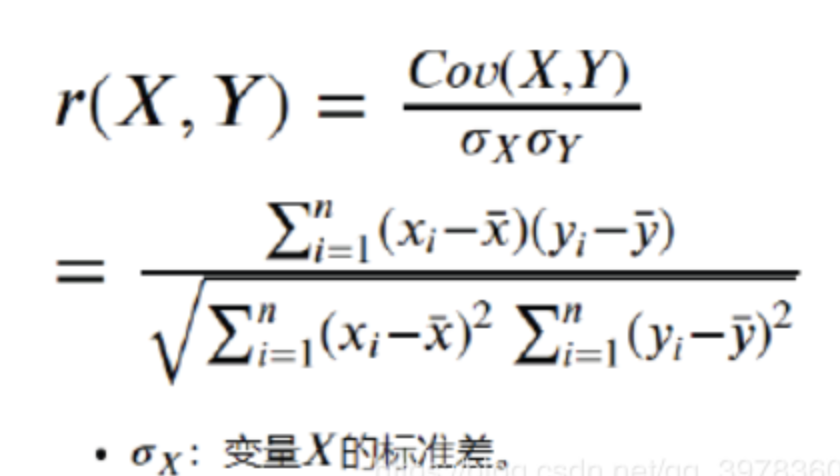
公式含义：就是用X、Y的协方差除以X的标准差和Y的标准差。
统计学中常用相关系数 r 来表示两变量之间的相关关系。
相关系数 r 的取值范围为[-1,1]，我们可以根据相关系数的取值来衡量两个变量的相关性
绝对值： 0.8~1.0 极强相关
0.6~0.8 强相关
0.4~0.6 中等程度相关
0.2~0.4 弱相关
0.0~0.2 极弱相关或无相关
正数：正相关性
负数：负相关性
相关系数优点：协方差可大可小不好衡量，所以用相关系数取值稳定。
# 计算协方差和相关系数 不推荐 x = data["AQI"] y = data["Precipitation"] # 计算AQI与Precipitation的协方差。 a = (x - x.mean()) * (y - y.mean()) cov = np.sum(a) / (len(a) - 1) print("协方差：", cov) # 计算AQI与Precipitation的相关系数。 corr = cov / np.sqrt(x.var() * y.var()) print("相关系数：", corr)
# 协方差：协方差体现的是两个变量之间的分散性以及两个变量变化步调是否一致。容易得知，当协方差的两个变量相同时，协方差就是方差。 # 相关系数，可以用来体现两个连续变量之间的相关性，最为常用的为皮尔逊相关系数 # 计算协方差和相关系数 推荐 # Series中已经提供好了计算协方差和相关系数的方法cov(),corr() x = data["AQI"] y = data["Precipitation"] print("协方差：", x.cov(y)) print("相关系数：", x.corr(y))
DataFrame中提供了计算相关系数的方法
data.corr()
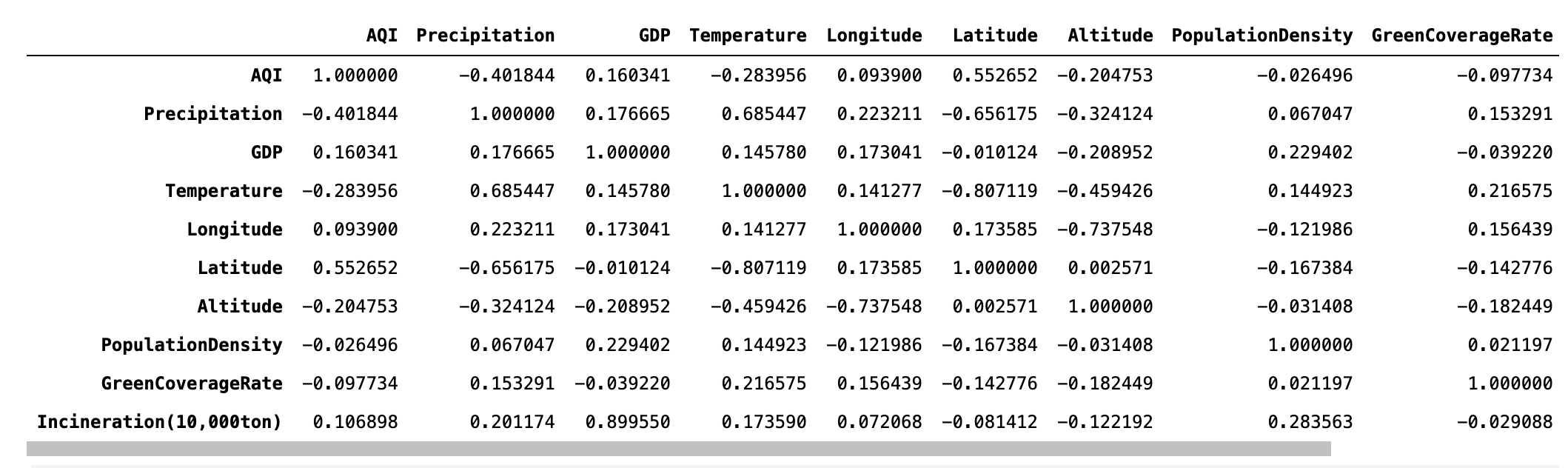
用热力图来更清晰的呈现相关系数值
# 用热力图来更清晰的呈现相关系数值 plt.figure(figsize=(15, 10)) # annot=True:显示数值 False:不显示数值 # fmt=".2f":保留两位小数 ax = sns.heatmap(data.corr(), cmap=plt.cm.RdYlGn, annot=True, fmt=".2f") # 注意：Matplotlib 3.1.1版本的bug，heatmap的首行与末行会显示不全。 # 可手动调整y轴的范围来进行修复。（老版本的Matplotlib不需要调整y轴范围。） # a, b = ax.get_ylim() # ax.set_ylim(a + 0.5, b - 0.5) # “经度”【longitude】、“纬度”【 Latitude】
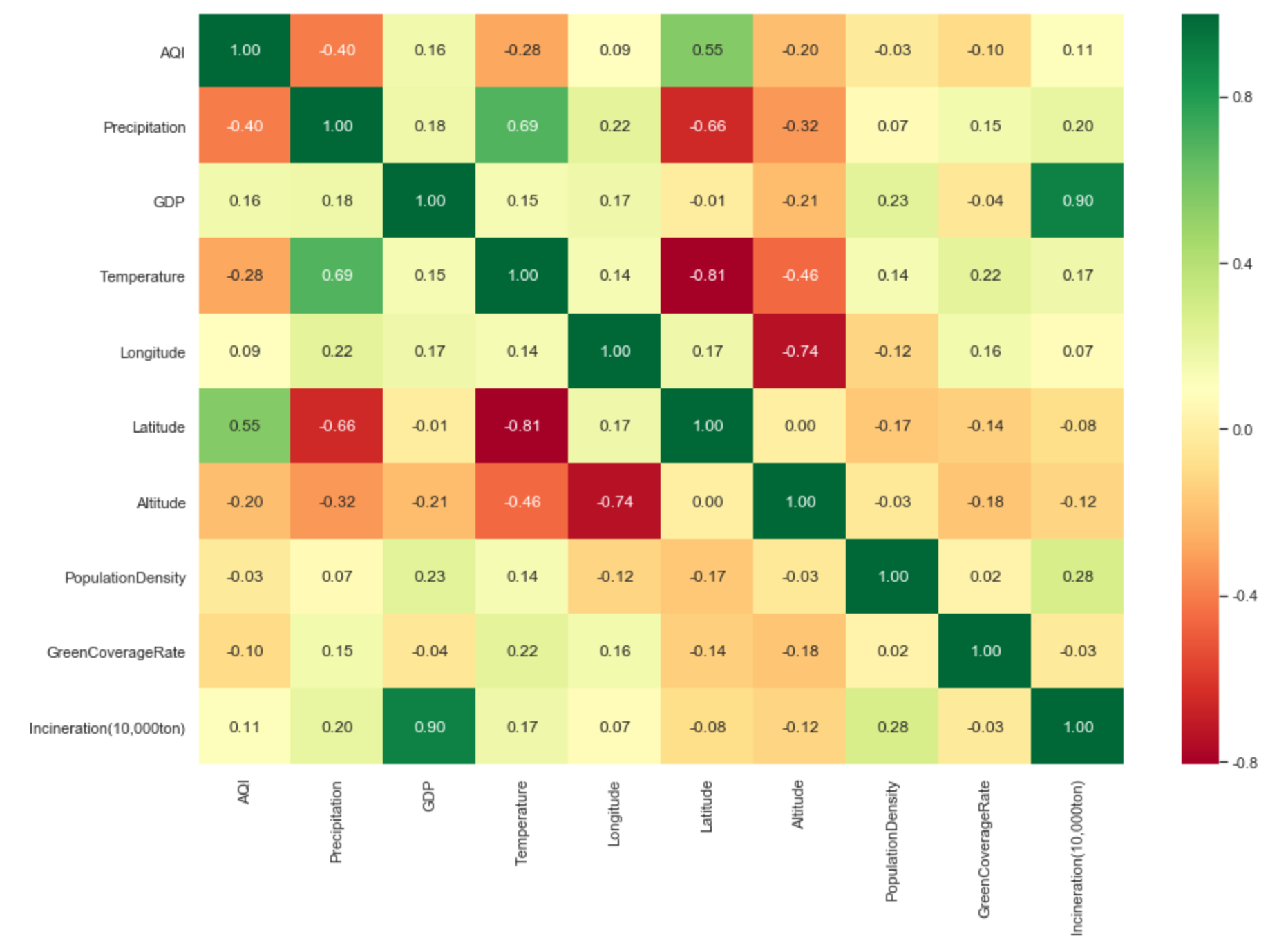
从结果可知，空气质量指数主要受降雨量（-0.40）与维度（0.55）影响。
- 降雨量越多，空气质量越好。
- 维度越低，空气质量越好
当然还可以发现其他结论：GDP与Incineration(10,000ton)正相关（0.90）
temputer与Precipitation正相关（0.69）
temputer与Latitude负相关（-0.81）等等。
6.5 全国空气质量的验证
验证全国的空气质量指数均值在71左右 （总体）
t检验验证：原假设 全国空气质量均值为71
# 我们使用单样本t检验 r = stats.ttest_1samp(data["AQI"], 71) print("t值：", r.statistic) print("p值：", r.pvalue) # P值大于0.05,所有无法拒绝原假设，故接受原假设
所以我们维持原假设，但不一定代表原假设就一定正确，只不过我们没有充足的理由去推翻它。
tf分布计算置信区间的正确方法：
(不能用均值加减1.96倍方差)
# t分布的置信区间 # 严格意义上来说不能用均值加减1.96倍标准差,因为当样本容量较大时,t分布近似正态分布,但当样本容量较小时,二者有较大差异 mean = data["AQI"].mean() std = data["AQI"].std() stats.t.interval(0.95, df=len(data) - 1, loc=mean, scale=std / np.sqrt(len(data))) # 71在这个区间，所以维持原假设
7. 对空气质量进行预测
机器学习心理路程 --通用的思路 但不是绝对的 不能学太死板
数据转换
# Series中的map函数 可以实现数据的替换 data["Coastal"] = data["Coastal"].map({"是": 1, "否": 0}) data["Coastal"].value_counts()
此时1，0没有大小区别 因为还可以使用其他值 都可以拟合出w
二分类变量：可以转换为任意两个离散变量
多分类变量（>=3个）：不能将n个类别映射为0，1，2，...n-1 ，会增加真实的差异性
类别变量：用独热编码（one-hot）
| x1 | x2 | x3 | |
|
w1 |
1 | 0 | 0 |
| w2 | 0 | 1 | 0 |
| w3 | 0 | 0 | 1 |
基模型
# 首先建立一个基模型 后续操作在此模型上进行操作 from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split X = data.drop(["City","AQI"], axis=1) y = data["AQI"] # 用线性回归进行训练 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) lr = LinearRegression() lr.fit(X_train, y_train) print("训练集：",lr.score(X_train, y_train)) print("测试集：",lr.score(X_test, y_test))
线性回归预测
# 线性回归预测 () y_hat = lr.predict(X_test) plt.figure(figsize=(15, 5)) plt.plot(y_test.values, "-r", label="真实值", marker="o") plt.plot(y_hat, "-g", label="预测值", marker="D") plt.legend(loc="upper left") plt.title("线性回归预测结果", fontsize=20)
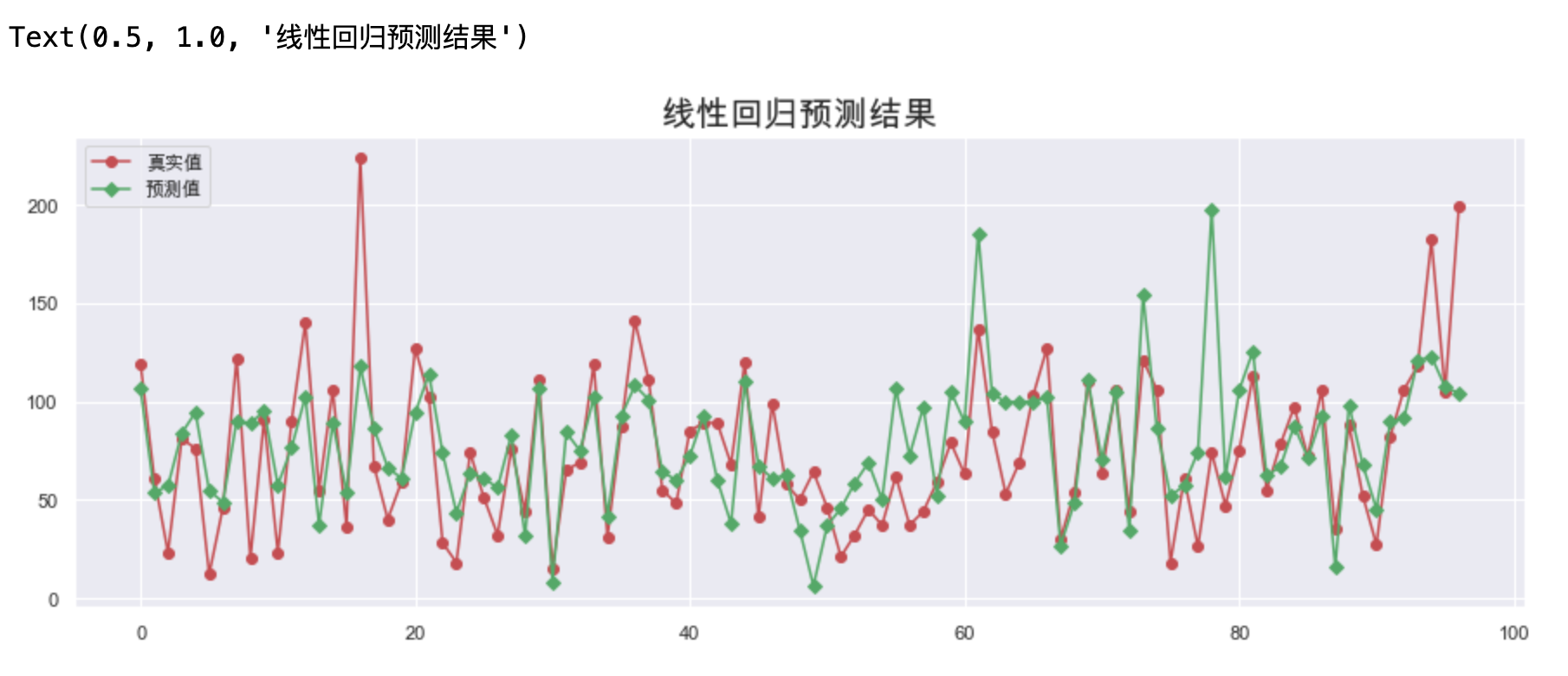
特征选择
--去除没有用处的特征
# 特征选择是一门非常重要的技术
# 特征并非越多越好，有些特征可能对模型质量没有很大改善，我们可以进行删除，同时也能够提高模型训练速度
# RFECV：递归特征消除，包含RFE和CV
# RFE阶段：递归特征消除
# CV阶段：交叉验证，避免偶然性
from sklearn.feature_selection import RFECV # estimator： 要操作的模型。 # step： 每次删除的变量数。 # cv： 使用的交叉验证折数。（把数据分成几份） # n_jobs： 并发的数量。-1表示把所有的CPU来进行并发 # scoring: 评估的方式。这里采用的是R方 rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2") # 进行训练 rfecv.fit(X_train, y_train) # 返回经过选择之后，剩余的特征数量。 print("经过选择之后，剩余的特征数量：",rfecv.n_features_) # 返回经过特征选择后，使用缩减特征训练后的模型。 print("经过特征选择后，使用缩减特征训练后的模型：",rfecv.estimator_) # 返回每个特征的等级，数值越小，特征越重要。 print("每个特征的等级：",rfecv.ranking_) # 返回布尔数组，用来表示特征是否被选择。 print("特征：",X.columns) print("返回布尔数组，用来表示特征是否被选择",rfecv.support_) # 返回对应数量特征时，模型交叉验证的评分。 print("返回对应数量特征时，模型交叉验证的评分",rfecv.grid_scores_)
绘制 特征数量与交叉验证$R^2$值的关系
plt.plot(range(1, len(rfecv.grid_scores_) + 1), rfecv.grid_scores_, marker="o") plt.xlabel("特征数量") plt.ylabel("交叉验证$R^2$值")
经过特征选择之后，8个特征训练的模型跟全部10个特征训练的模型无论在训练集还是测试集的表现上，都几乎相同，这就可以证明,清楚这两个目标确实对拟合目标(y值)没有什么帮助，可以去掉。
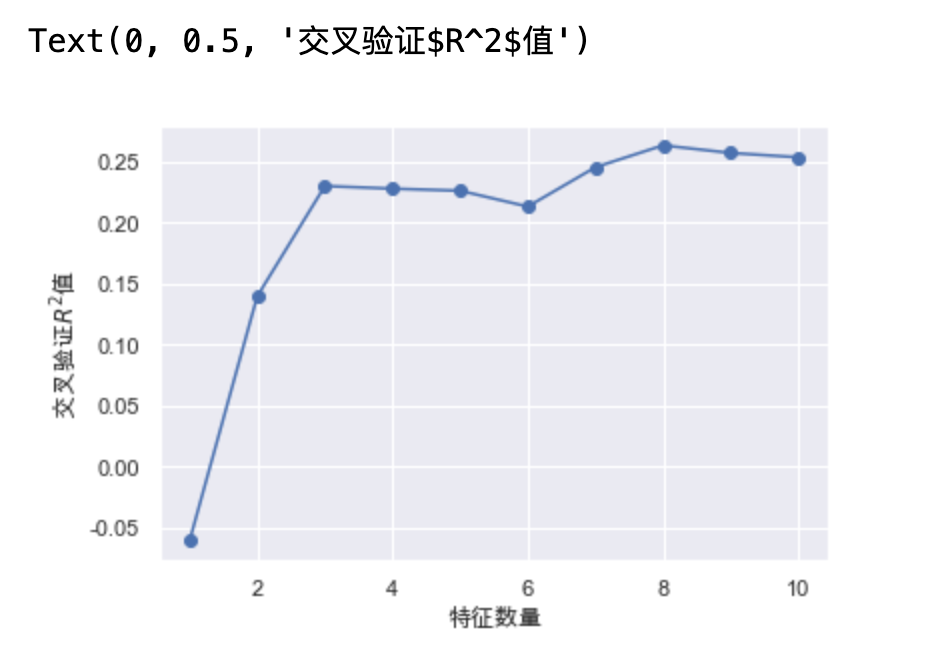
print("剔除的变量：", X_train.columns[~rfecv.support_]) print("保留的变量：", X_train.columns[rfecv.support_]) # 只保留剩下的那8个特征 X_train_eli = rfecv.transform(X_train) X_test_eli = rfecv.transform(X_test) print(rfecv.estimator_.score(X_train_eli, y_train)) print(rfecv.estimator_.score(X_test_eli, y_test))
异常值处理
--临界值替换
使用箱线图判断离群点，然后使用临界值替换异常值
我们应该使用训练集的数据去计算临界值
--除了类别变量的列外，其他所有的列都需要异常值处理
# 使用箱线图判断离群点，然后使用临界值替换异常值 # 我们应该使用训练集的数据去计算临界值 # Coastal是类别变量，映射为离散变量，不会有异常值。查看除了Coastal之外有没有异常值 for col in X.columns.drop("Coastal"): # is_numeric_dtype：查看类别是否是数值类型的，是的话就继续往下 if pd.api.types.is_numeric_dtype(X_train[col]): # 计算1/4分位和3/4分位 IQR 下限和上限 quartile = np.quantile(X_train[col], [0.25, 0.75]) IQR = quartile[1] - quartile[0] lower = quartile[0] - 1.5 * IQR upper = quartile[1] + 1.5 * IQR # 替换 训练集和测试集都要替换 X_train[col][X_train[col] < lower] = lower X_train[col][X_train[col] > upper] = upper X_test[col][X_test[col] < lower] = lower X_test[col][X_test[col] > upper] = upper
去除异常值后使用新的训练集和测试集来评估模型的效果
# 去除异常值后使用新的训练集和测试集来评估模型的效果 lr.fit(X_train, y_train) print(lr.score(X_train, y_train)) print(lr.score(X_test, y_test))
消除异常值之后再使用RFECV方法
# 消除异常值之后再使用RFECV方法 rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2") rfecv.fit(X_train, y_train) print(rfecv.n_features_) print(rfecv.ranking_) print(rfecv.support_) print(rfecv.grid_scores_) plt.plot(range(1, len(rfecv.grid_scores_) + 1), rfecv.grid_scores_, marker="o") plt.xlabel("特征数量") plt.ylabel("交叉验证$R^2$值")
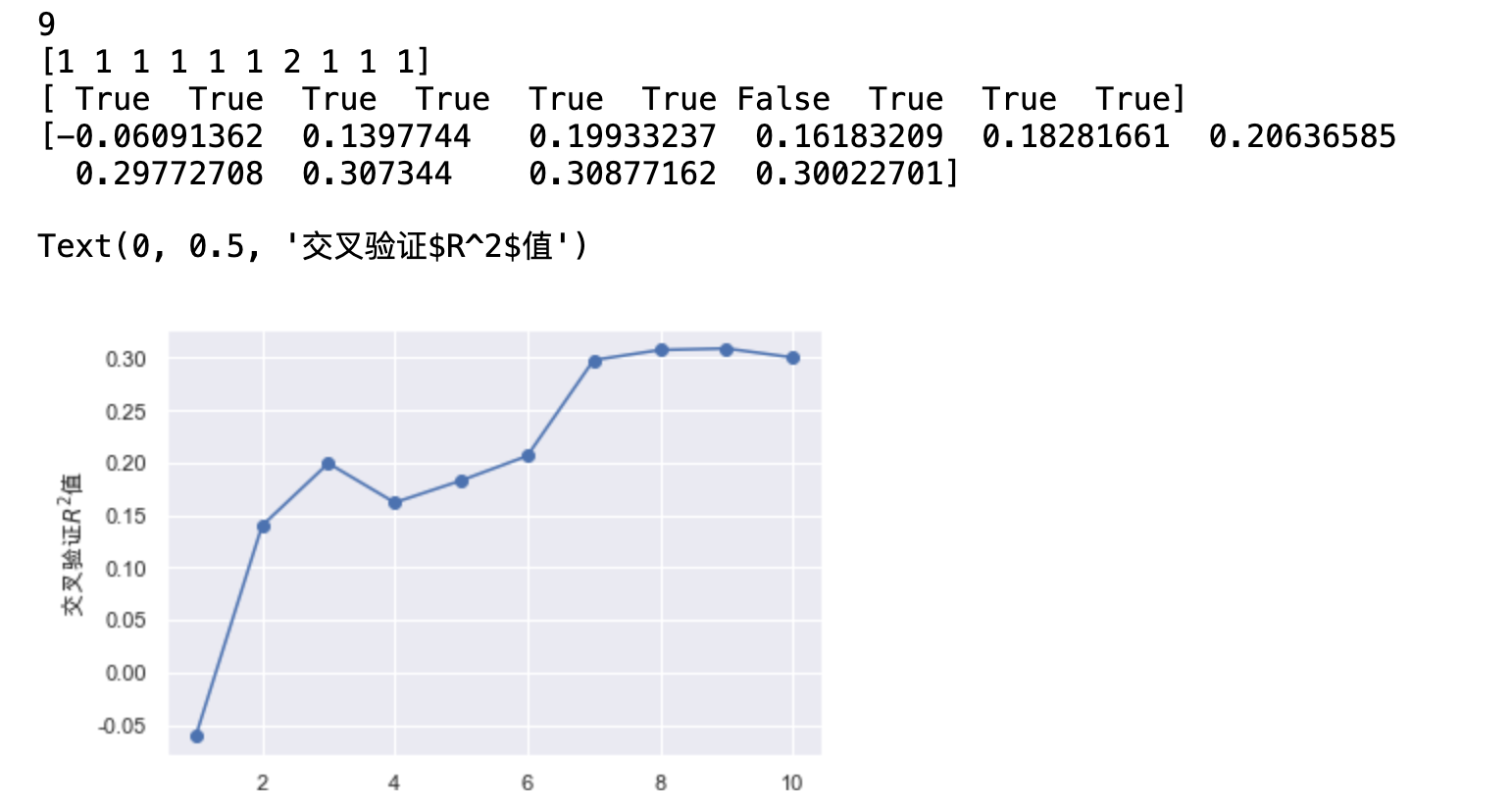
我们发现 9个特征的时候交叉验证得到的效果最好
print("剔除的变量：", X_train.columns[~rfecv.support_]) # 得到ndarry # X_train_eli = rfecv.transform(X_train) # X_test_eli = rfecv.transform(X_test) # 为了方便后面列的筛选操作，这里我们换一种方式转换。 # 得到DataFrame类型，可保留列名 X_train_eli = X_train[X_train.columns[rfecv.support_]] X_test_eli = X_test[X_test.columns[rfecv.support_]] print(rfecv.estimator_.score(X_train_eli, y_train)) print(rfecv.estimator_.score(X_test_eli, y_test))
分箱操作 --原则：x对y是阶梯式的影响，而不是线性的
分箱后，我们不能将每个区间映射为离散数值，而是应当使用One-Hot编码
难点：哪些特征需要分箱操作需要去试或者查询！
分箱的个数需要去尝试，区间跨度比较大可以设置大点的值，还有如果值的跨度很大才有影响可以把个数设置少一点。
from sklearn.preprocessing import KBinsDiscretizer # KBinsDiscretizer K个分箱的离散器。用于将数值（通常是连续变量）变量进行区间离散化操作。 # n_bins：分箱（区间）的个数。--是尝试之后设置的可以调整。--对应的是discretize中传过来的 # encode：离散化编码方式。分为：onehot，onehot-dense与ordinal。 # onehot：使用独热编码，返回稀疏矩阵。只存1 不存0 # onehot-dense：使用独热编码，返回稠密矩阵。1和0都存 # ordinal：使用序数编码（0,1,2……）。 # strategy：分箱的方式。分为：uniform，quantile，kmeans。 # uniform：每个区间的长度范围大致相同。 # quantile：每个区间包含的元素个数大致相同。 # kmeans：使用一维kmeans方式进行分箱。 k = KBinsDiscretizer(n_bins=[4, 5, 14, 6], encode="onehot-dense", strategy="uniform") # 定义离散化的特征。 # 阶梯式的改变才采用分箱离散化,n_bins=[4, 5, 14, 6]这四个是老师试出来的，我们也可以试试其他的
discretize = ["Longitude", "Temperature", "Precipitation", "Latitude"] r = k.fit_transform(X_train_eli[discretize]) r = pd.DataFrame(r, index=X_train_eli.index) # 获取除离散化特征之外的其他特征。 X_train_dis = X_train_eli.drop(discretize, axis=1) # 将离散化后的特征与其他特征进行重新组合。 X_train_dis = pd.concat([X_train_dis, r], axis=1) # 对测试集进行同样的离散化操作。 r = pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index) X_test_dis = X_test_eli.drop(discretize, axis=1) X_test_dis = pd.concat([X_test_dis, r], axis=1) # 查看转换之后的格式。 display(X_train_dis.head())
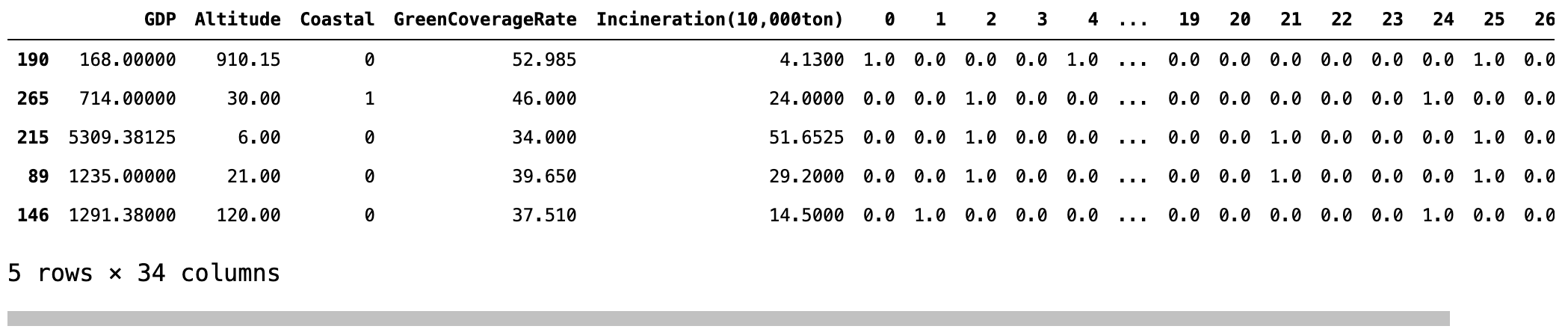
对转换后的数据进行训练
# 对转换后的数据进行训练 lr.fit(X_train_dis, y_train) print(lr.score(X_train_dis, y_train)) print(lr.score(X_test_dis, y_test)) # 离散后 模型效果有了提升
残差分析
残差图分析 --残差：模型预测值与真实值之间的差异
异方差性
好的回归模型 误差应该是随机分布的 残差值就应该随机分布在中心线附近，如果我们从残差图中找出规律，说明我们遗漏了某些能够影响残差的解释信息。
异方差性：残差具有明显的方差不一致性。
fig, ax = plt.subplots(1, 2) fig.set_size_inches(15, 5) data = [X_train, X_train_dis] title = ["原始数据", "处理后数据"] for d, a, t in zip(data, ax, title): model = LinearRegression() model.fit(d, y_train) y_hat_train = model.predict(d) residual = y_hat_train - y_train.values a.set_xlabel("预测值") a.set_ylabel(" 残差") a.axhline(y=0, color="red") #正中间那根红线 a.set_title(t) sns.scatterplot(x=y_hat_train, y=residual, ax=a) #画出散点图
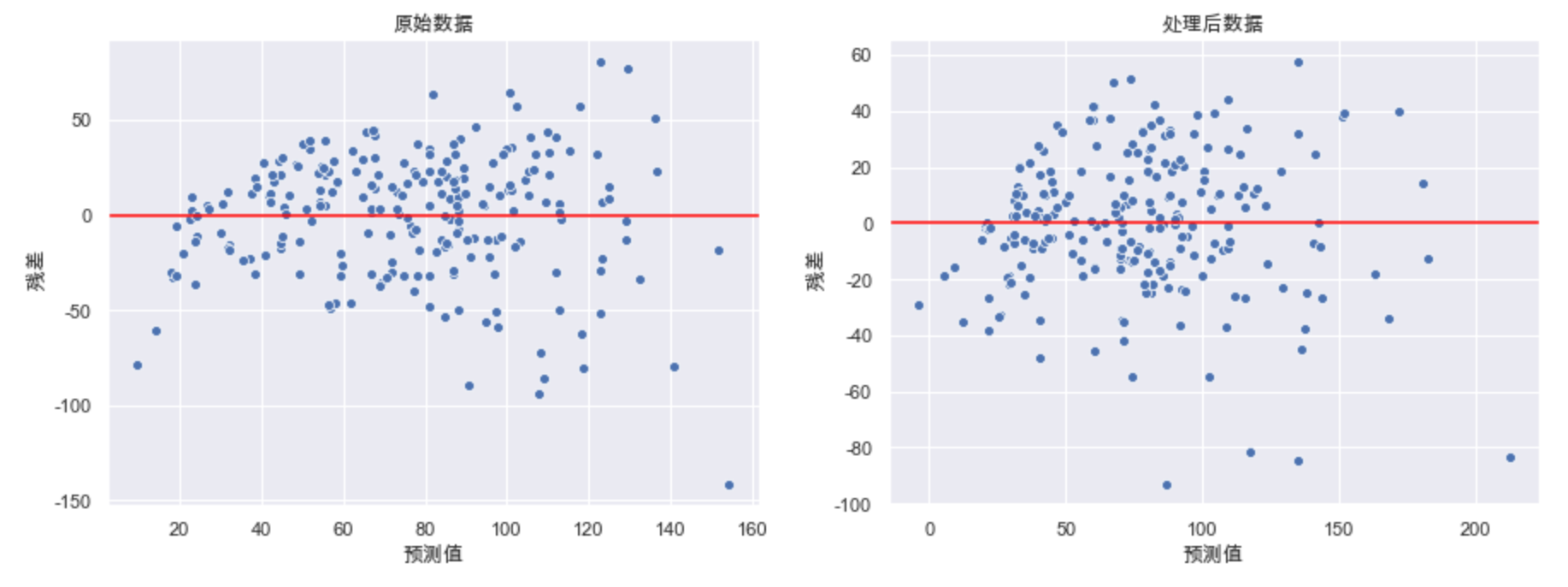
如果我们处理后的数据存在这种异方差性那么就需要进行处理
左图中我们发现，随着预测值的增大，模型的误差也在增大，对于此种情况，我们可以使用对目标y值取对数的方式处理
# 出现了异方差性 措施：对目标y值取对数的方式处理 model = LinearRegression() y_train_log = np.log(y_train) y_test_log = np.log(y_test) model.fit(X_train, y_train_log) y_hat_train = model.predict(X_train) residual = y_hat_train - y_train_log.values plt.xlabel("预测值") plt.ylabel(" 残差") plt.axhline(y=0, color="red") sns.scatterplot(x=y_hat_train, y=residual) # 异方差性得到解决 模型的效果也会得到一定的提升
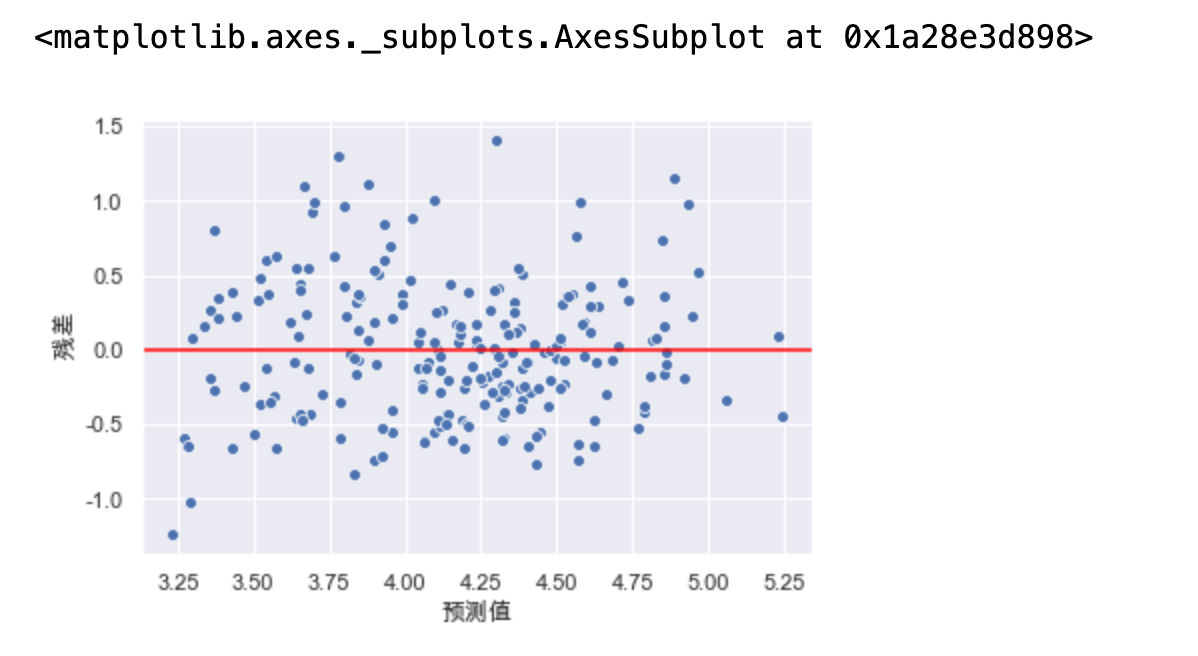
我们可以通过绘制残差图，通过预测值和实际值之间的关系，来检测离群点（异常值）
# 通过绘制残差图 来检测离群点 y_hat_train = lr.predict(X_train_dis) residual = y_hat_train - y_train.values r = (residual - residual.mean()) / residual.std() plt.xlabel("预测值") plt.ylabel(" 残差") plt.axhline(y=0, color="red") sns.scatterplot(x=y_hat_train[np.abs(r) <= 2], y=residual[np.abs(r) <= 2], color="b", label="正常值") sns.scatterplot(x=y_hat_train[np.abs(r) > 2], y=residual[np.abs(r) > 2], color="orange", label="异常值")
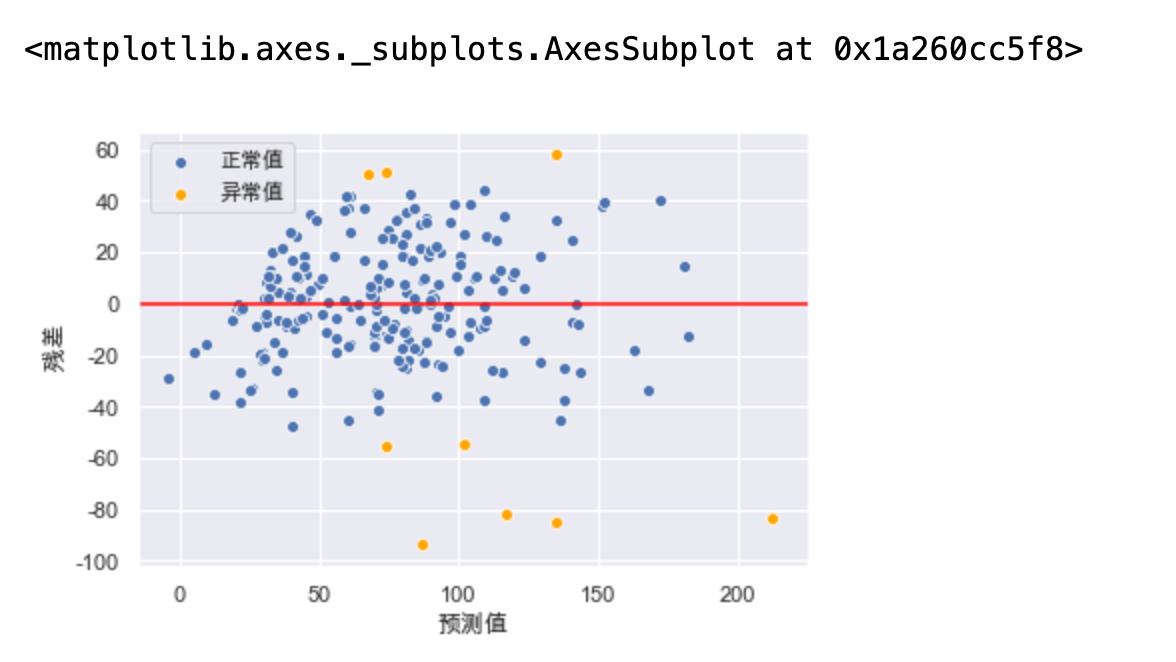
# 对转换后的数据进行训练 X_train_dis_filter = X_train_dis[np.abs(r) <= 2] y_train_filter = y_train[np.abs(r) <= 2] lr.fit(X_train_dis_filter, y_train_filter) print(lr.score(X_train_dis_filter, y_train_filter)) print(lr.score(X_test_dis, y_test)) # 训练集得到了提升
可以看出训练集得到了很好的提升，但是测试集还是相差无几 ，但这不失为一种考虑方案。
最后得出结论：
哪些城市的空气质量较好：Shaoguan，Nanping，Meizhou，Keelung，Sanming。
空气质量在地理位置上是否具有一定的规律性：空气质量总体分布上来说，南方城市优于北方城市，西部城市优于东部城市。
临海城市的空气质量是否有别于内陆城市：临海城市的空气质量优于内陆城市。
空气质量主要受哪些因素影响：是否临海，降雨量，维度对空气质量影响较大。
全国城市空气质量普遍处于何种水平：我国空气质量95%的概率在(70.63, 80.04)之间。
怎样预测一个城市的空气质量：通过历史数据，我们可以对空气质量进行预测。
种一棵树最好的时间是十年前 其次是现在
