ROC与AUC的定义与使用详解
分类模型评估:
| 指标 | 描述 | Scikit-learn函数 |
|---|---|---|
| Precision | 精准度 | from sklearn.metrics import precision_score |
| Recall | 召回率 | from sklearn.metrics import recall_score |
| F1 | F1值 | from sklearn.metrics import f1_score |
| Confusion Matrix | 混淆矩阵 | from sklearn.metrics import confusion_matrix |
| ROC | ROC曲线 | from sklearn.metrics import roc |
| AUC | ROC曲线下的面积 | from sklearn.metrics import auc |
回归模型评估:
| 指标 | 描述 | Scikit-learn函数 |
|---|---|---|
| Mean Square Error (MSE, RMSE) | 平均方差 | from sklearn.metrics import mean_squared_error |
| Absolute Error (MAE, RAE) | 绝对误差 | from sklearn.metrics import mean_absolute_error, median_absolute_error |
| R-Squared | R平方值 | from sklearn.metrics import r2_score |
ROC和AUC定义
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)。ROC曲线的面积就是AUC(Area Under the Curve)。AUC用于衡量“二分类问题”机器学习算法性能(泛化能力)。
计算ROC需要知道的关键概念
首先,解释几个二分类问题中常用的概念:True Positive, False Positive, True Negative, False Negative。它们是根据真实类别与预测类别的组合来区分的。
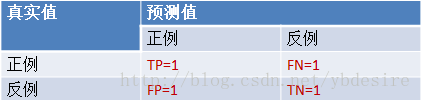
假设有一批test样本,这些样本只有两种类别:正例和反例。机器学习算法预测类别如下图(左半部分预测类别为正例,右半部分预测类别为反例),而样本中真实的正例类别在上半部分,下半部分为真实的反例。
- 预测值为正例,记为P(Positive)
- 预测值为反例,记为N(Negative)
- 预测值与真实值相同,记为T(True)
- 预测值与真实值相反,记为F(False)
-
-
TP:预测类别是P(正例),真实类别也是P FP:预测类别是P,真实类别是N(反例)TN:预测类别是N,真实类别也是NFN:预测类别是N,真实类别是P
样本中的真实正例类别总数即TP+FN。TPR即True Positive Rate,TPR = TP/(TP+FN)。
同理,样本中的真实反例类别总数为FP+TN。FPR即False Positive Rate,FPR=FP/(TN+FP)。
还有一个概念叫”截断点”。机器学习算法对test样本进行预测后,可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3,一般我们认为概率低于0.5,t1就属于类别N。这里的0.5,就是”截断点”。
总结一下,对于计算ROC,最重要的三个概念就是TPR, FPR, 截断点。
截断点取不同的值,TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线,就是ROC曲线。横轴用FPR表示。
sklearn计算ROC
sklearn给出了一个计算ROC的例子[1]。
-
y = np.array([1, 1, 2, 2])
-
scores = np.array([0.1, 0.4, 0.35, 0.8])
-
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
- 1
- 2
- 3
- 1
- 2
- 3
通过计算,得到的结果(TPR, FPR, 截断点)为
-
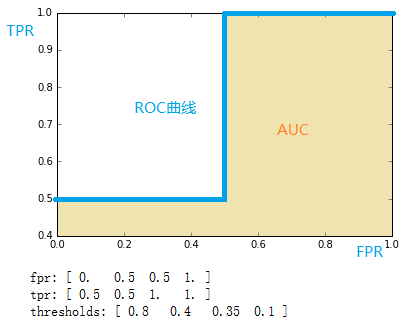
fpr = array([ 0. , 0.5, 0.5, 1. ])
-
tpr = array([ 0.5, 0.5, 1. , 1. ])
-
thresholds = array([ 0.8 , 0.4 , 0.35, 0.1 ])#截断点
- 1
- 2
- 3
- 1
- 2
- 3
将结果中的FPR与TPR画到二维坐标中,得到的ROC曲线如下(蓝色线条表示),ROC曲线的面积用AUC表示(淡黄色阴影部分)。
详细计算过程
上例给出的数据如下
-
y = np.array([1, 1, 2, 2])
-
scores = np.array([0.1, 0.4, 0.35, 0.8])
- 1
- 2
- 1
- 2
用这个数据,计算TPR,FPR的过程是怎么样的呢?
1. 分析数据
y是一个一维数组(样本的真实分类)。数组值表示类别(一共有两类,1和2)。我们假设y中的1表示反例,2表示正例。即将y重写为:
y_true = [0, 0, 1, 1]- 1
- 1
score即各个样本属于正例的概率。
2. 针对score,将数据排序
| 样本 | 预测属于P的概率(score) | 真实类别 |
|---|---|---|
| y[0] | 0.1 | N |
| y[2] | 0.35 | P |
| y[1] | 0.4 | N |
| y[3] | 0.8 | P |
3. 将截断点依次取为score值
将截断点依次取值为0.1,0.35,0.4,0.8时,计算TPR和FPR的结果。
3.1 截断点为0.1
说明只要score>=0.1,它的预测类别就是正例。
此时,因为4个样本的score都大于等于0.1,所以,所有样本的预测类别都为P。
-
scores = [0.1, 0.4, 0.35, 0.8]
-
y_true = [0, 0, 1, 1]
-
y_pred = [1, 1, 1, 1]
- 1
- 2
- 3
- 1
- 2
- 3
TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 1
3.2 截断点为0.35
说明只要score>=0.35,它的预测类别就是P。
此时,因为4个样本的score有3个大于等于0.35。所以,所有样本的预测类有3个为P(2个预测正确,1一个预测错误);1个样本被预测为N(预测正确)。
-
scores = [0.1, 0.4, 0.35, 0.8]
-
y_true = [0, 0, 1, 1]
-
y_pred = [0, 1, 1, 1]
- 1
- 2
- 3
- 1
- 2
- 3
TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 0.5
3.3 截断点为0.4
说明只要score>=0.4,它的预测类别就是P。
此时,因为4个样本的score有2个大于等于0.4。所以,所有样本的预测类有2个为P(1个预测正确,1一个预测错误);2个样本被预测为N(1个预测正确,1一个预测错误)。
-
scores = [0.1, 0.4, 0.35, 0.8]
-
y_true = [0, 0, 1, 1]
-
y_pred = [0, 1, 0, 1]
- 1
- 2
- 3
- 1
- 2
- 3
TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0.5
3.4 截断点为0.8
说明只要score>=0.8,它的预测类别就是P。所以,所有样本的预测类有1个为P(1个预测正确);3个样本被预测为N(2个预测正确,1一个预测错误)。
-
scores = [0.1, 0.4, 0.35, 0.8]
-
y_true = [0, 0, 1, 1]
-
y_pred = [0, 0, 0, 1]
- 1
- 2
- 3
- 1
- 2
- 3
TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0
心得
用下面描述表示TPR和FPR的计算过程,更容易记住
- TPR:真实的正例中,被预测正确的比例
- FPR:真实的反例中,被预测正确的比例
最理想的分类器,就是对样本分类完全正确,即FP=0,FN=0。所以理想分类器TPR=1,FPR=0。









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人