之手算KD-tree
转自:https://zhuanlan.zhihu.com/p/27453420
数据集:
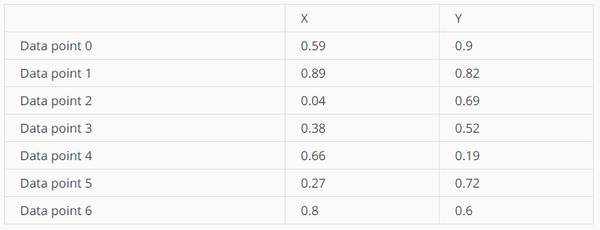

kd-tree构建过程:
第一步:进行第一次split
从上图可以看出,X轴的方差更大一些,所以先从X轴进行split。split value取point 1和point 2的平均值,即(0.89+0.04) / 2 = 0.465
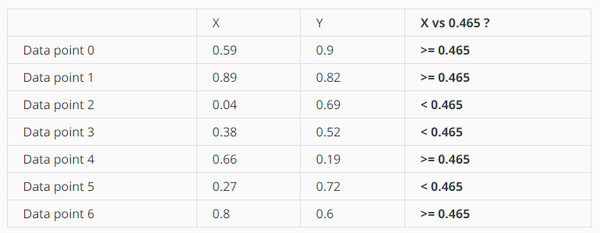
分成如下两个结点:


在每个结点,我们记录下它的tight coordinate bound,这个是为了在查询的时候剪枝用的。
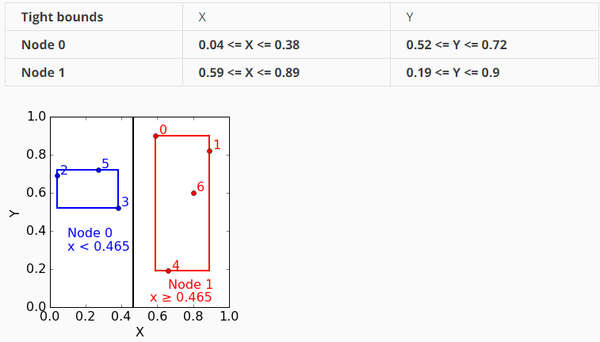
这个时候,这棵树的样子:

第二步:递归进行split
我们先来确定我们用的启发式方法:
a.选择哪个轴进行split?方差大的,或者还没有使用过的轴
b.如何确定split value:(smallest value + biggest value) / 2
c.什么时候stop?在本例子中选择node只含有<=2个point的时候
因为第一次是用的x轴split,为了充分利用信息,第二次使用y轴split


现在就树是这个样子了:

同样对node 1进行split:
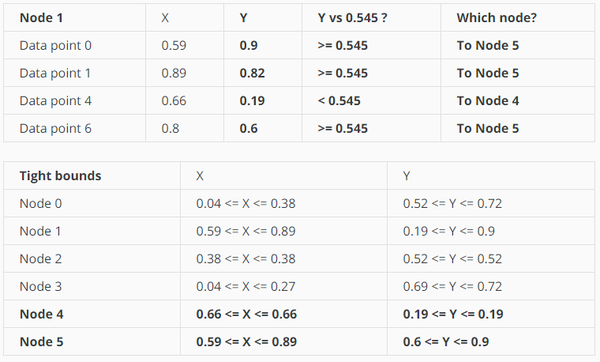
树变成这个样子:
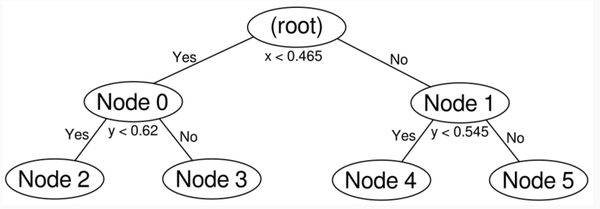
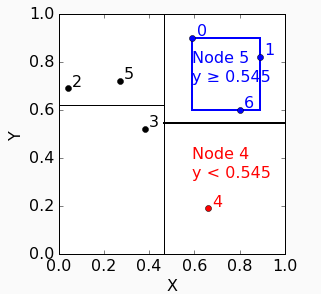
因为node 5的point有3个,所以需要继续split,因为上次用Y轴split,所以这次用x轴。
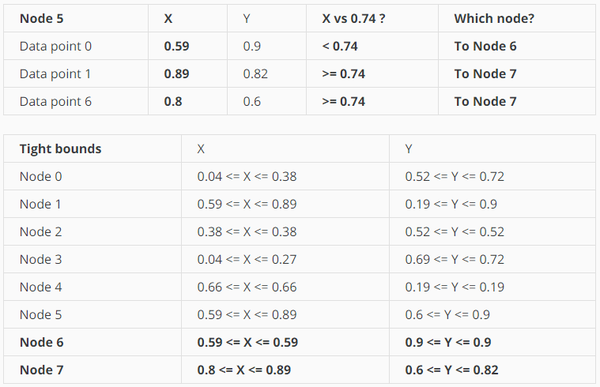
最终的树:
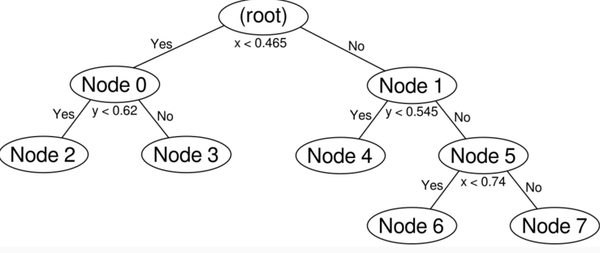
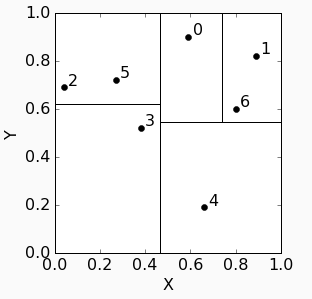
kd-tree查询过程:
比如我们的query point是红色点:

从kdtree里可以找到属于node 6:

它到data point 0的距离是0.256,所以最近邻居一定出现在以0.256为半径的圆里。
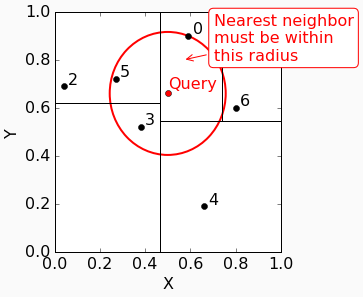
我们来tranverse back:
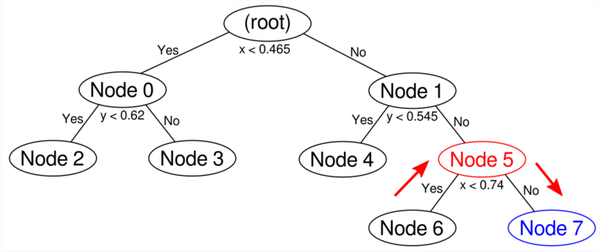
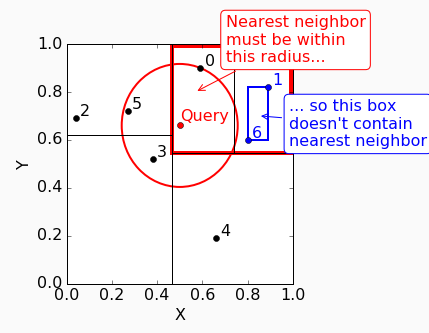
但是node7的tight bounding box并不在圆里,所以prune掉。
继续向上找:
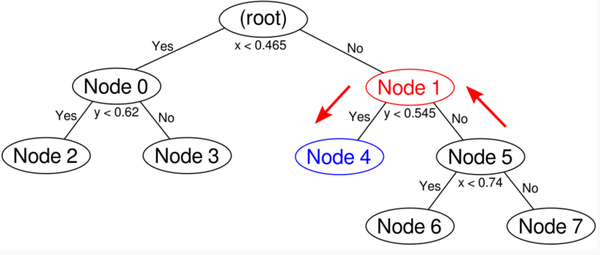

node4只有一个点,而这个点不在圆里,prune掉。
继续tranverse:
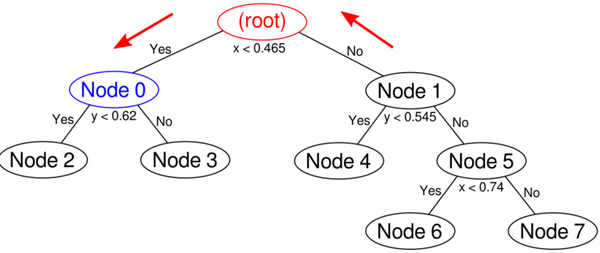
node0包含两个结点,node0本身在圆里,所以就想看node2和node3

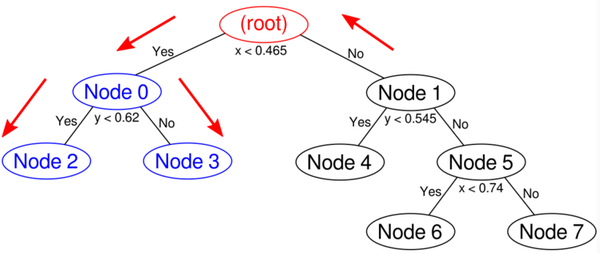
计算node2和node3到query point的距离:
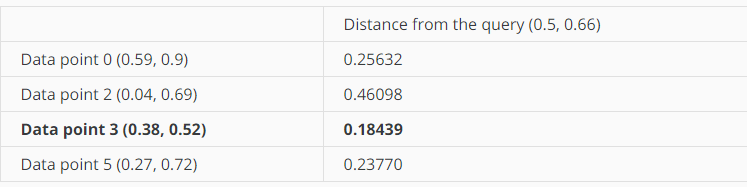
这个时候data point3到query point的距离最小,而已缩小搜索圆了,搜索圆的半径减小到0.18439。
这个时候继续搜索,但是所有结点都搜索完了,所以data point3是最近邻。
作者:白菜菜白
出处:http://www.cnblogs.com/lvchaoshun/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



