高效学习--隐马尔可夫过程

 找到了一个比较好的隐马尔可夫过程教程，我翻译并记录一下。

参考链接：https://docs.google.com/presentation/d/16fz6fAUjLo6YEb5diOja7kHSuBLT94dh9mxWNqksaMk/edit#slide=id.g14260a3a4f_0_28

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    今天给大家介绍隐马尔可夫模型是什么，以及它是如何工作的， 并介绍它在数据科学方面的应用。

对于那些以前来过这里,你知道之前的图森数据科学组的聚会主要专注于深度学习,即人工神经网络,

虽然跟上前沿技术很重要,摘要是非常重要的知道,因为他们已经存在了很长时间,仍然坚持使用NLP等许多领域的研究人员,特别是在生物信息学。

HMM 是一个机器重要的方法因为它已经存在了相当长的时间，并且现在仍然在很多例如NLP和生物信息学等领域广泛使用.

 

看完这篇博客之后你会对HMM有一个深入的理解，如何使用它，以及可以应用它解决什么类型的问题。

首先回顾一下马尔可夫过程，马尔可夫链，HMM的结构和算法，最后来一个python 的例子。

首先，我们看一下HMM的历史发展.

HMM 是 马尔可夫模型的一种， 但是HMM背后的数学原理要追溯到19世纪末， 当时一个俄罗斯数学家 安德烈•马尔可夫 开始对马尔可夫过程,马尔可夫链等进行理论研究。

安德烈•马尔可夫和他的同事(Русла́нСтрато́нович)也对随机微积分的发明作出了贡献!

除此之外，HMMs在20世纪50年代末和60年代首次被系统性的描述，到70年代和80年代已经被用于语音识别和生物信息学等领域。

由于HMMs已经被使用了很长时间，因此学习这套理论是非常与必要的，尤其是在需要使用深度学习的,一些比较新的工作上。

HMM在这些领域持续的应用也不断证明了HMM的有效性。

 

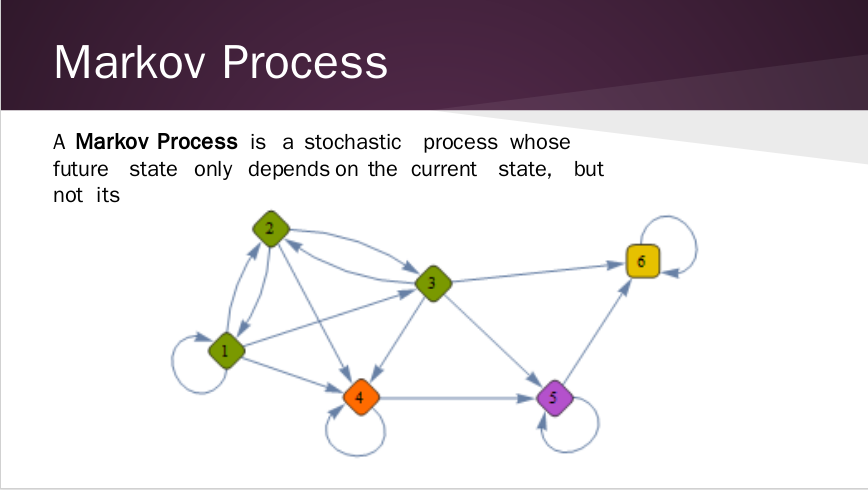
让我们从讨论马尔可夫过程开始，这是HMMs和其他马尔可夫模型所具有的一个非常重要的特性。

看上面这个图，假设我有一个序列，1 2 3 4 5 6

根据马尔可夫过程，当我从一个状态遍历到下一个状态时，我在估计下个状态时只考虑当前状态。

也就是说，如果我现在在点2，然后移动到点4，我就不再需要考虑从点1开始的事实。

简单说就是，一个马尔可夫过程假定下一时刻的状态仅取决与当前状态而与之前的状态无关。

----------------------

 事件A和B,

$P(A, B)$

$P(X_1 = x_1, X_2 = x_2)$

可以分解为：

$P(A, B) = P(A) * P(B|A)$
同理：

$P(X_1 = x_1, X_2 = x_2) = P(X_1 = x_1) * P(X_2 = x_2|X_1 = x_1)$

 

假设有随机变量序列：${x_1, x_2, ... x_n}$ 长度 $n$ 固定。

 

Goal: model of joint probability distribution over values of variables $|V|^n$ different possibilities

 

Now before we look at Hidden Markov Models, its important to understand a Markov Chain, so we can become familiar with states and transition matrixes.  To do this, let’s imagine an example with the states “A” and “B”. At any given time, I am in state A or B, but I can never be in both. Now if we look at this figure, we can see that there are these arrows coming from the states. These arrows represent the transition probabilities. So if we look at A, the orange arrow here means that If i am in state A, I have a 30% chance of staying in state A, and a 70% chance of moving to state B. If this example isn’t concrete enough for you, let me pitch this to you with a more concrete example.
Imagine this Markov Chain represents a driver model for an auto insurance company.
State A means that you’re an  ‘High risk’ driver and state B means you’re a ‘Low risk’ driver. We’ll see here that ‘high risk’ means that you’ve got a ticket during the year.
So when you first start your insurance, the company might put you in group B for ‘Low risk’. Now what this means is that if you start as a low risk driver, you have a 60 percent chance of staying a lost risk driver for a year, and a 40% chance of becoming a high risk driver.
Update year by year. Will you stay a low risk driver or will you become a
As you will see, these Markov models are all sensitive to time.

Now, this trellis graph here can also be represented as this matrix. They’re the exact thing.

----------------------------
For this example let’s consider auto insurance

Each year if you have/haven’t had a ticket, you are placed into a group (low risk, high risk)

Adds to 100

A “state” is simply the category a motorist can be in in any given time

IMPORTANT: ONLY TELLS US PROBABILITY OF MOVING STATE TO STATE.

DOES NOT tell us anything about probability of STARTING in either state. We don’t know what it is right now.

Can find probability of being at any state for any step of the process. So if you’ve been with that insurance company for 10 years, you can find out the probability of being high or low risk 10 years from now.

Can do predictions far into the future

Markov Chains are handy

Moving from state to state through steps

ALL TRANSITION PROBABILITIES COMING OUT OF A STATE ADD TO 1!

P(ABB) = 0.7*0.6*0.6

 

MATRIX

Each sums to 1