【RAY TRACING THE REST OF YOUR LIFE 超详解】 光线追踪 3-6 直接光源采样

 

Chapter7 Sample Lights Directly

 

 Preface

今天我们来讲这个还算牛逼的技术——直接光源采样

之前我们提到过，在2-7

 

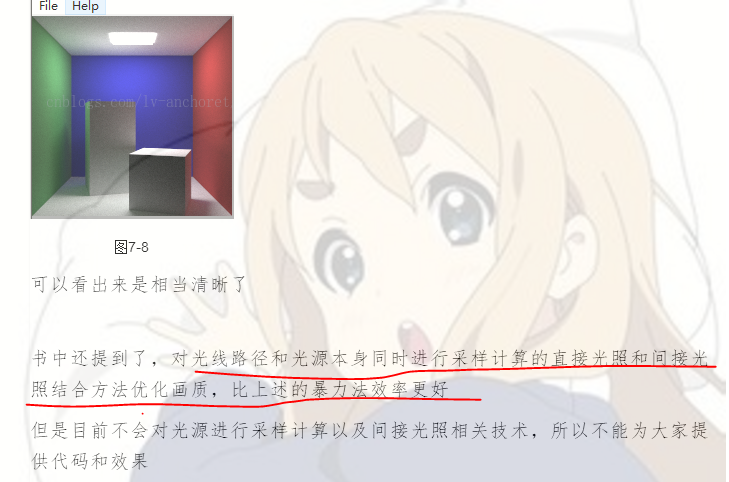
前两篇我们也提到要减少噪点，就是图片上的黑点点，所以，所有的矛头都指向了这一篇。

简单说一下为什么会有那么多小点点，就是因为光线路径中没有触碰到光源，路径计算之后就会是黑色的点，可以通过发射大量的光线，比如计算每个像素点的时候发射8k~1w条采样光线进行路径计算；也可以路径计算方面做文章，比如加深路径计算递归深度；等等诸如此类。但是上述方法都是暴力解决法，相当耗时，我们可以运用数学对其进行优化，从而实现画质和效率的双面提升，这就是我们今天要讲的——直接光源采样！

 

 Ready

可能您需要以下基础：

1.微分

2.立体角 （蒙特卡罗（三））

没了，剩下全靠想象

 

 content

简明扼要。

我们朝光源方向发送光线或者生成朝向光源的随机方向都是很容易实现的，但是我们需要知道的是，pdf（direction）是什么呢？

引用书上一张图：

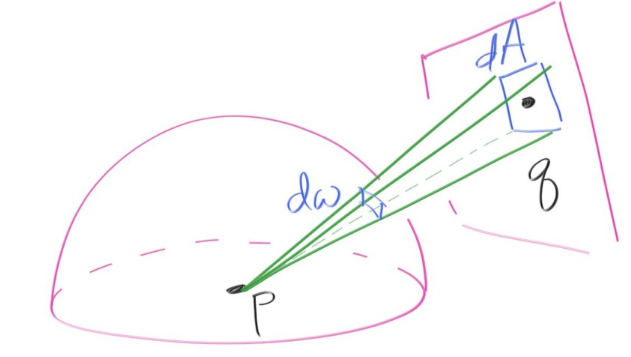
对于一个光源区域A，如果我们均匀采样该区域，那么这个pdf就等于1/A，意思就是每个点的概率均等

但是和我们的单位球体结合在一起的话，就比较麻烦了，见上图

？为什么老是提到单位球体呢？？

因为我们的光线和物体表面的交点，会作为下一个eye，然后新的视线方向是表面单位球随机产生的方向，具体见1-5中的diagram7-3

 

 

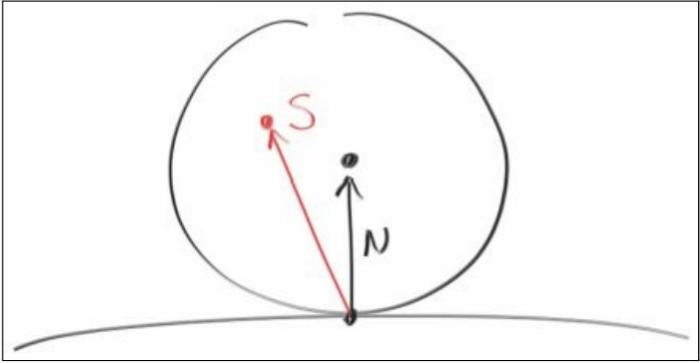
好了，渊源就是酱紫，我们继续

如果那个小的微分区域dA的采样概率为

　　p_q(q)*dA（采样比例乘以微分区域）,也就是dA/A

而对应到单位球体表面的很小的区域，即我们所述的方位角。方位角微分dΩ对应的采样概率为

　　p(direction)*dΩ

这里有一个用来描述dΩ 和 dA 的表达式：

dΩ = dA cosα / （distance（p,q）^2）

即：方位角微分区域：光源微分区域分成（球心到A中心距离平方）份，取其中的cosα代表的份额数

因为这个dA 和 dΩ的概率是相同的，所以就有如下等式

p(direction) * cosα * dA / (distance(p,q)^2) = p_q(q) * dA = dA / A

所以

p(direction) = distance(p,q)^2 / (cosα * A)

 

我们接下来就检验一下这个数学公式是否正确

但是代码可能非常丑

我们需要之前的光源的区域参数

 

    list[cnt++] = new xz_rect(200, 350, 220, 340, 550, light);

 

 

 

所以我们有以下的代码

 

rtvec lerp(const ray& sight, intersect* world, int depth)
{
    hitInfo info;
    if (world->hit(sight, (rtvar)0.001, rtInf(), info))
    {
        ray scattered;
        rtvec emitted = info._materialp->emitted(info._u, info._v, info._p);
        rtvar pdf;
        rtvec albedo;
        if (depth < 50 && info._materialp->scatter(sight, info, albedo, scattered, pdf))
        {
            rtvec on_light = rtvec(213 + lvgm::rand01() * (343 - 213), 554, 227 + lvgm::rand01() * (332 - 227));
            rtvec to_light = on_light - info._p;
            double distance_squared = to_light.squar();
            to_light.self_unitization();
            if (dot(to_light, info._n) < 0)    
                return emitted;
            double light_area = (343 - 213)*(332 - 227);
            double light_cosine = fabs(to_light.y());
            if (light_cosine < 1e-6)    
                return emitted;
            pdf = distance_squared / (light_cosine*light_area);
            scattered = ray(info._p, to_light, sight.time());
            return emitted + albedo *info._materialp->scatter_pdf(sight, info, scattered)*lerp(scattered, world, depth + 1) / pdf;
        }
        else
            return emitted;
    }
    else
        return rtvec();
}

 

 

 

如下图：

 

因为我们一路做测试，做图形分析对比，所以我们上图是sample为250时候的效果

据说，sample为10时，效果依旧很好

所以又超快速运行了一个sample为10的

 

不管怎样，我们的图形噪点已经做到了比较不错的境地了，sample为10！！！

再看看之前的sample为250的图形效果

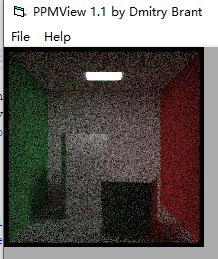
简直噪出天际线

 

关于本篇的那个图

天花板上灯光周围的噪声是由于灯光是双面的，灯光和天花板之间有一个狭窄空间。

我们可以通过将灯光法向量调至垂直向下来解决这一问题，同时让我们的灯光发射函数也做相应的处理

    virtual rtvec emitted(const ray& rIn, const hitInfo& info, const rtvar u, rtvar v, const rtvec& p)const 
        {
        if(dot(info._n,rIn.direction())<0.)
            return _emit->value(u, v, p); 
        else 
            return rtvec();
        }

 

记得一起改了material基类，以及lerp的emit函数调用根据上述参数描述

所以我们又得到了一个sample为10的新图

没什么大的变化

只是灯光周围的噪点少了，解释：

因为灯光的法向量垂直向下，而我们的反射光线与反射之后与法向量的夹角为锐角的时候才进行纹理计算

而来自屋顶上面的光线与灯光区域碰撞反射的方向与法向量呈钝角（注意是反射之后的新方向不是入射光方向）则不计算返回黑色，默认光无法到达

 

感谢您的阅读，生活愉快~