【Ray Tracing The Next Week 超详解】 光线追踪2-7 任意长方体 && 场景案例
上一篇比较简单,很久才发是因为做了一些好玩的场景,后来发现这一章是专门写场景例子的,所以就安排到了这一篇
Preface
这一篇要介绍的内容有:
1. 自己做的光照例子
2. Cornell box画质问题及优化方案
3. 新的场景几何体——长方体
轴平行长方体
任意长方体
我们这一篇重实践轻理论阐述
ready
1. 需要上一章的知识
但是,上一章的Cornell box画质优化仅限于盒子本身,如果作为场景和其他物体放在一起就不能那么优化画质
即,Cornell box像素计算失败应该返回黑色点而非白色
2. 需要图形学基本仿射变换知识
3. 玻璃球镂空技术,如有忘记,请移步此处
先看效果
光照案例
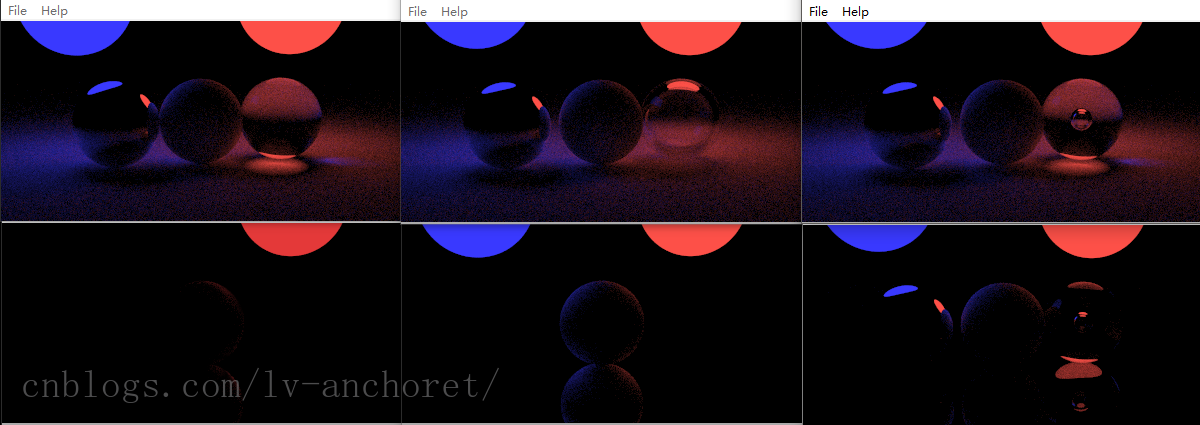
图7-1

Cornell box案例(最初步)

图7-2
最终版

任意轴旋转
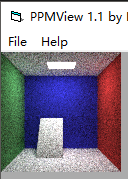

正文
学了光照就迫不及待地整了一堆东西
终于脱开了蓝色插值背景转到正儿八经的光了
在还没学长方形之前,就先用球体做了光源
注:坐标轴按照光线追踪坐标系描述(y轴位于垂直向上方向,z轴垂直屏幕向外)
1. 图7-1 第二行左
该图是最开始的一张图,相机仍然在(13,3,2),第一卦限
而球体是一个半径为1的漫反射白球,置于原点处
下面仍然是一个大的镜面球(metal),y轴-1000处,半径999,正好和小球相切
红色灯光则置于第三卦限,例如:(-3,3,-3)
整个场景的背景为黑色,即光线路径计算失败后返回黑色
如上,则会看到球体表面有一抹红色的色泽,然后大球镜面反射也有一部分
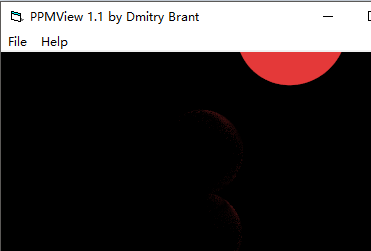
图7-3
2. 图7-1 第二行中
在上图的基础上添加一个位于第四卦限的蓝色光源
就会形成漫反射球左侧为蓝色表面光泽右侧为红色表面光泽的效果
3. 图7-1 第一行左
上面两个当然很没意思了,但是一直以来都是蓝色背景亮堂堂的,第一次黑不溜秋的地方用灯照着东西,感觉挺真实的,光线追踪效果也很不错,所以上面两张图是新世纪的开端!
我们在(0,0,2)处,放一个半径为1的镜面球,在原点对称处放一个半径为1的玻璃球
下面的大球改为漫反射
哇,想想就刺激,结果不出所料
镜面球在黑乎乎的环境下只映出了蓝色光源和红色光源,以及旁边的漫反射球的相关部分,而玻璃球就更有意思了,透了红光照在漫反射大球表面上,还透了微弱的蓝光,也照在了右侧的地面上
4. 图7-1 第一行中
突然想到一个绝妙的主意,玻璃球可以镂空
于是设置了一个镂空球(0,0,-2),半径为-0.8
之后,想着把镜面球和磨砂小球离远一点,再观察磨砂小球在镜面球中的影,于是乎就成了上面这张图
镜面球依旧映这磨砂小球和灯光的影,然而玻璃球只有上面一丝丝的明亮,着实看着不尽人意
可能是镂空的太多了,于是有了右边那张图
5. 图7-1 第一行右
把镂空球半径设置小一点,想了想就-0.2吧
果然,不负吾望,还真是着实好看,不仅可以往地上透光,形状更有意思,像个立体环!!
其实,我是想调一个把左边两个特点合二为一的图,即既有第一张图的底面透光,又有第二图上表面那个明亮的高光
6. 图7-1 第二行右
其实是为了凑齐6张图,思来想去,没啥整的了,老是调个镂空半径没啥意思,渲染时间还长,后来想了下,不如把大球改成原来的镜面,这样下面三张图都是镜子大地,上面三张都是磨砂大地
于是乎,emmm,貌似还完成了上面提到的梦想,上表面”高光”以及底面的透光,不仅如此,而且镂空内表面还有透光,还映在了大地上,强无敌嘞~
上述场景代码
intersect* light() { texture * perlintex = new noise_texture(6.3); material* redlight = new areaLight(new constant_texture(rtvec(0.98, 0.1, 0.08))); material* bluelight = new areaLight(new constant_texture(rtvec(0.05, 0.05, 1.))); intersect**list = new intersect*[7]; list[0] = new sphere(rtvec(-2, 3, -3), 1.5, redlight); list[1] = new sphere(rtvec(-2.2, 3.2, 2.8), 1.5, bluelight); list[2] = new sphere(rtvec(0, 0, 2.2), 1, new metal(new constant_texture(rtvec(1, 1, 1)))); list[3] = new sphere(rtvec(), 1, new lambertian(new constant_texture(rtvec(1, 1, 1)))); list[4] = new sphere(rtvec(0, 0, -2), 1, new dielectric(1.5)); list[5] = new sphere(rtvec(0, 0, -2), -0.18, new dielectric(1.5)); list[6] = new sphere(rtvec(0, -1000, 0), 999, new dielectric(1.5)); return new intersections(list, 7); }
Chapter 7:Instance
我们来进行正常的章节学习,emmmm
现在先来学习轴平行的长方体,这个东西呢我知道的目前有两种方法
第一种是球坐标系下多个方位角和长宽高参数确定的长方体
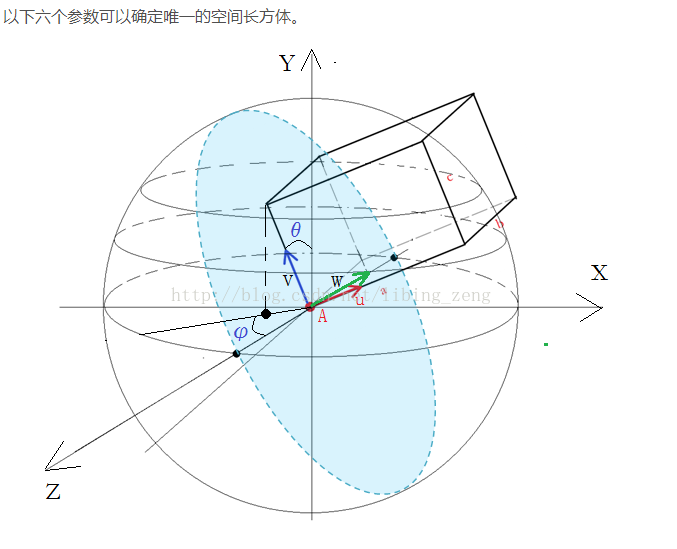
此图引用于https://blog.csdn.net/libing_zeng/article/details/54561605
如果想要学习的话可以去学习一下这种方法
第二种方法自然就是顶点确定形体,左下-右上顶点确定形体,不仅适用于2D的形,同样适用于3D的体
心里罗列一下我们现有的零件,是否能够整一个长方体出来,好像可以
我们已经弄好了长方形,那么就可以粘成长方体
不错,只要把各个长方形的法线指向外部即可,而第一种方法也要求取每个面的法线
所以,我们这种方法还是比较好的,毕竟我们就是用6个法线构建的,第一种还需要方位角转换运算求取
那么我们就写成了如下代码
/// box.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the box-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { // the statement of box class class box: public intersect { public: box() { } box(const rtvec& pointmin, const rtvec& pointmax, material * mat); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: rtvec _min; rtvec _max; intersect* _list; }; // the implementation of box class inline box::box(const rtvec& pointmin, const rtvec& pointmax, material * mat) :_min(pointmin) ,_max(pointmax) { intersect ** list = new intersect*[6]; list[0] = new xy_rect(_min.x(), _max.x(), _min.y(), _max.y(), _max.z(), mat); list[1] = new flip_normal(new xy_rect(_min.x(), _max.x(), _min.y(), _max.y(), _min.z(), mat)); list[2] = new xz_rect(_min.x(), _max.x(), _min.z(), _max.z(), _max.y(), mat); list[3] = new flip_normal(new xz_rect(_min.x(), _max.x(), _min.z(), _max.z(), _min.y(), mat)); list[4] = new yz_rect(_min.y(), _max.y(), _min.z(), _max.z(), _max.x(), mat); list[5] = new flip_normal(new yz_rect(_min.y(), _max.y(), _min.z(), _max.z(), _min.x(), mat)); _list = new intersections(list, 6); } bool box::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { return _list->hit(sight, t_min, t_max, info); } aabb box::getbox()const { return aabb(_min, _max); } } // rt namespace
根据最小点坐标和最大点坐标构建六个面
于是我们来做开篇第二张图

在上一篇文章的Cornell box的场景中添加上面两个box
如果你的代码中,上一篇的仍然是背景为白色(即光线路径计算失败后返回白色)
那么将是下面这个
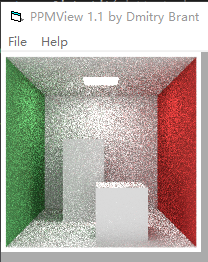
图7-4
面向我们的两个物体面是光线追踪几乎计算不到的地方,所以基本是纯白色
我们迫不得已再把背景改为黑色

如第34行所示
但是我们一想到上一篇的一堆黑点噪声就。。。真是把一张美图糟蹋了

图7-5
如何优化呢?
思来想去,有下列几种方法
1. 把区域光面积调大
2. 把光源与顶部距离调大,因为房间的每一面墙壁都是边长为555的正方形,敢问,距离为一个像素的光如何把偌大的平面照亮,于是乎,我改成了距离5....
3. 相机距离房间门口800像素,我们调为700像素
则修改后的图像为:
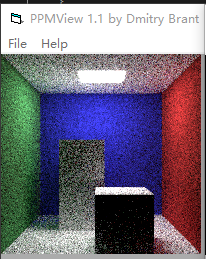
图7-6
还有一个最重要的改进方式,增加采样点,即增加光线条数
可以对比,sample为10的时候(之前是sample为100)
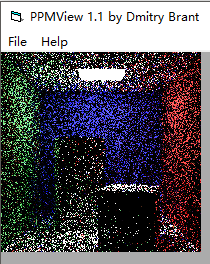
图7-7
从《Ray Tracing From the Ground Up》中得知,最简单粗暴的方法是发出万条光线做路径计算可以得到我们想要的图片
于是我将sample改为了2w,跑了一夜,现在是这样的

图7-8
可以看出来是相当清晰了
书中还提到了,对光线路径和光源本身同时进行采样计算的直接光照和间接光照结合方法优化画质,比上述的暴力法效率更好
但是目前不会对光源进行采样计算以及间接光照相关技术,所以不能为大家提供代码和效果
好了,我们继续章节学习——旋转和平移
我们知道,平移比较简单,但是在光线追踪中如何实现物体平移呢?
它并没有顶点集合,它只有一个几何体方程以及碰撞检测,怎么平移呢
对了,就是碰撞检测这里!
我们对每一个碰撞点进行变换计算,也就把整个理想化的物体实例化且做了变换
1. 平移
对于平移,我们可以对每个碰撞点进行移动也可以在计算碰撞点的时候把eye往反方向移动,进而,求取碰撞点,也可以实现平移
我们采取第二种
/// translate.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the translate-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { class translate :public intersect { public: translate(intersect* p, const rtvec& offset); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: intersect* _item; rtvec _offset; }; translate::translate(intersect* p, const rtvec& offset) :_item(p) , _offset(offset) { } bool translate::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { ray movedRay(sight.origin() - _offset, sight.direction(), sight.time()); if (_item->hit(movedRay, t_min, t_max, info)) { info._p += _offset; return true; } return false; } aabb translate::getbox()const { aabb box = _item->getbox(); return aabb(box.min() + _offset, box.max() + _offset); } }// rt namespace
这个比较简单
2. 旋转
我们来复习一下图形学中仿射变换的知识
关于旋转:(引用书上一张图)
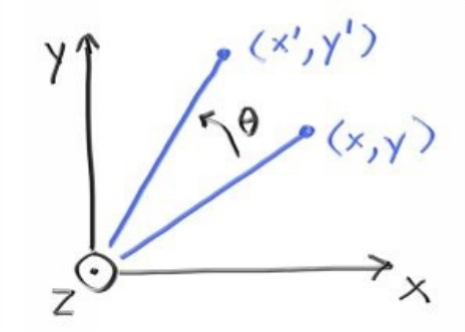
则
x' = cosθ * x - sinθ * y y' = sinθ * x + cosθ * y
那么写成惯用的矩阵形式(采用列向量表示法),则是(绕z轴转)
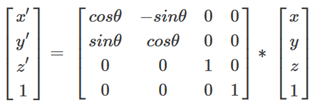
同理,绕y轴转:
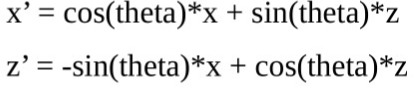
绕x轴转:
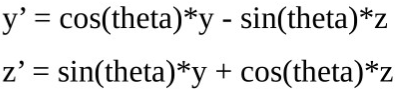
那么,我们来写绕y轴转的类
/// rotate.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the rotate-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { // the statement of rotate class class rotate :public intersect { public: rotate(intersect* p, rtvar angle); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: intersect* _item; rtvar _sinθ; rtvar _cosθ; aabb _box; }; // the implementation of rotate class rotate::rotate(intersect* p, rtvar angle) :_item(p) { rtvar radians = (π / 180.) * angle; _sinθ = sin(radians); _cosθ = cos(radians); rtvec min(rtInf(), rtInf(), rtInf()); rtvec max = -min; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) { rtvar x = i * _box.max().x() + (1 - i)*_box.min().x(); rtvar y = j * _box.max().y() + (1 - j)*_box.min().y(); rtvar z = k * _box.max().z() + (1 - k)*_box.min().z(); rtvar newx = _cosθ * x + _sinθ * z; rtvar newz = -_sinθ * x + _cosθ * z; rtvec tester(newx, y, newz); for (int c = 0; c < 3; ++c) { if (tester[c] > max[c]) max[c] = tester[c]; if (tester[c] < min[c]) min[c] = tester[c]; } } _box = aabb(min, max); } bool rotate::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { rtvec eye = sight.origin(); rtvec direction = sight.direction(); eye[0] = _cosθ * sight.origin()[0] - _sinθ * sight.origin()[2]; eye[2] = _sinθ * sight.origin()[0] + _cosθ * sight.origin()[2]; direction[0] = _cosθ * sight.direction()[0] - _sinθ * sight.direction()[2]; direction[2] = _sinθ * sight.direction()[0] + _cosθ * sight.direction()[2]; ray rotatedRay(eye, direction, sight.time()); if (_item->hit(rotatedRay, t_min, t_max, info)) { rtvec p = info._p; rtvec n = info._n; p[0] = _cosθ * info._p[0] + _sinθ * info._p[2]; p[2] = -_sinθ * info._p[0] + _cosθ * info._p[2]; n[0] = _cosθ * info._n[0] + _sinθ * info._n[2]; n[2] = -_sinθ * info._n[0] + _cosθ * info._n[2]; info._p = p; info._n = n; return true; } return false; } aabb rotate::getbox()const { return _box; } } // rt namespace
我们来写图7-7的场景
intersect* Cornell() { intersect ** list = new intersect*[9]; size_t cnt = 0; material * red = new lambertian(new constant_texture(rtvec(0.65, 0.05, 0.05))); material * blue = new lambertian(new constant_texture(rtvec(0.05, 0.05, 0.73))); material * white = new lambertian(new constant_texture(rtvec(0.88, 0.88, 0.88))); material * green = new lambertian(new constant_texture(rtvec(0.12, 0.45, 0.15))); material * light = new areaLight(new constant_texture(rtvec(20, 20, 20))); list[cnt++] = new flip_normal(new yz_rect(0, 555, 0, 555, 555, green)); list[cnt++] = new yz_rect(0, 555, 0, 555, 0, red); list[cnt++] = new xz_rect(200, 350, 220, 340, 550, light); list[cnt++] = new flip_normal(new xz_rect(200, 350, 220, 340, 550, light)); list[cnt++] = new flip_normal(new xz_rect(0, 555, 0, 555, 555, white)); list[cnt++] = new xz_rect(0, 555, 0, 555, 0, white); list[cnt++] = new flip_normal(new xy_rect(0, 555, 0, 555, 555, blue)); list[cnt++] = new translate(new rotate(new box(rtvec(), rtvec(165, 165, 165), white), -18), rtvec(130, 0, 65)); list[cnt++] = new translate(new rotate(new box(rtvec(), rtvec(165, 330, 165), white), 15), rtvec(265, 0, 295)); return new intersections(list, cnt); }
图7-8是图7-7的高清版,暂时还没跑完,渲染完之后我在此处放上此场景的高清版,以及任意轴旋转的扩充代码
敬请期待。。。
**************************** 更新线 ******************************************
图7-8已经更新,程序终于跑完了
一张图片分了四部分一起跑还跑了两天,心累。。
感觉计算机也累,心疼1s
关于任意轴旋转
上述说明了y轴旋转的代码
旋转类中有三处需要做变换,向量运算也好,矩阵运算也罢
第一处是构造函数中的newx和newz(对称轴剩余两个分量)
第二处是hit函数中的eye运算和direction运算
第三处是hit函数中的p和n向量的运算
其中第一处和第三处用的是变换矩阵的原形(你可以先把上面的三个轴对应变换表达式转化为矩阵形式,如第一个的z轴旋转公式)
而第二处用的是对应变换矩阵的转置
如此续写其他两个轴的旋转类即可达成效果
当然你也可以写个场景测试一下
至于空间任意变换,无疑就是轴旋转和平移搭配结合所形成的效果
可以先在原点处构建物体,经多个轴旋转而后平移到目标位置以代替空间物体沿任意轴旋转的效果
场景测试代码

我们来对比一下各种采样数的效果对比
sample为100

sample为500
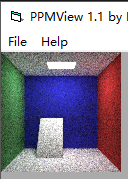
sample为1000(该场景为下一章的体积烟雾)

sample为20000

感谢您的阅读,生活愉快~

