【Ray Tracing The Next Week 超详解】 光线追踪2-3
Preface
终于到了激动人心的纹理章节了
然鹅,看了下,并不激动
因为我们之前就接触过
当初有一个 attenuation 吗?
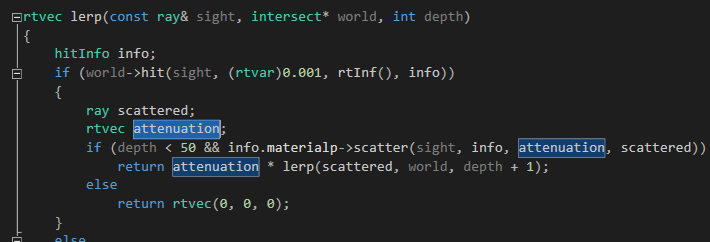
对了,这就是我们的rgb分量过滤器,我们画出的红色、蓝色、绿色等等,都是通过它来控制的
专业点的词语叫做rgb衰减比例,比如rtvec(1.,0.,0.),最后呈现出来的是红色,因为r保留了100%
它是怎么控制的呢,我们来回顾一下这个过程
首先,我们创建一个材质球

后面那个rtvec(0.4,0.2,0.1)就是衰减比例(衰减到原来的百分之。。)
之后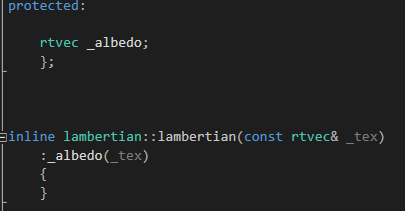
进入数据成员中,之后主函数调用lerp的时候
info.materialp->scatter(sight, info, attenuation, scattered))
球体的材质调用scatter函数
即:
没有丝毫改动地有数据成员传递到了attenuation 中
然后用attenuation 做乘法进行rgb衰减,递归就不用说了吧,最后递归到深处为黑色,不然为背景色
为什么要在前言将这个东东,因为
attenuation 所控制形成的物体表面颜色就是最简单的纹理
说白了这章比较简单,因为下一章是这本书的另外一个高难度章节(分别分布于第二章和第四章)
所以,中间第三章来点简单好玩的,过渡一下
先看效果

Chapter 3:Solid Textures
废话不多说,先写一个纹理类
/// texture.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the texture-class for the ray-tracing project // from the 《ray tracing the next week》 #pragma once namespace rt { class texture { public: virtual rtvec value(rtvar u, rtvar v, const rtvec& p)const = 0; }; }
u 和 v后面用到再讲,p就是衰减向量
然后写一个常量纹理(基础纹理)
/// constant_tex.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the constant_texture-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { class constant_texture :public texture { public: constant_texture() { } constant_texture(const rtvec& color); virtual rtvec value(rtvar u, rtvar v, const rtvec& p)const override; public: inline const rtvec& color()const { return _color; } private: rtvec _color; }; inline constant_texture::constant_texture(const rtvec& color) :_color(color) { } rtvec constant_texture::value(rtvar u, rtvar v, const rtvec& p)const { return _color; } }
之后,我们把材质中的rtvec向量改为纹理指针
/// diffuse.hpp // https://www.cnblogs.com/lv-anchoret/p/10198423.html // ----------------------------------------------------- // [author] lv // [begin ] 2018.12 // [brief ] one of the materials // ----------------------------------------------------- #pragma once
namespace rt { class texture; //diffuse material class lambertian : public material { public: lambertian(texture* _tex); virtual bool scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const override; protected: texture* _albedo; }; inline lambertian::lambertian(texture* _tex) :_albedo(_tex) { } bool lambertian::scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const { rtvec target = info._p + info._n + lvgm::random_unit_sphere(); scattered = ray{ info._p, target - info._p }; attenuation = _albedo->value(0.,0.,info._p); return true; } }
之前我们创建的材质球代码就要改一种风格了

把其他的材质类也做相应的改动
我们今天最重要的是弄棋盘(checkerboard)纹理
棋盘纹理就是交错的双色格子,呈现一定的规律性
所以我们想象一下利用某些映射函数来实现这种类似二值性,且呈现周期性
我们比较容易想到利用正余弦函数,呈现周期性,且值域为【-1,1】是个有界函数
如何体现二值呢,正负嘛,正余弦函数一定关于x轴对称
如何将物体表面和正余弦函数联系在一起形成双色交错的格子呢
我们采用每个点在3D空间中的位置来将两者联系在一起
综上,如果我们在所有三个维度中相乘某个正余弦函数,那么该公式的符号形成一个棋盘形式
即:rtvar sines = sin(10 * p.x()) * sin(10 * p.y()) * sin(10 * p.z());
当然,你也可以试一下sgnx函数,设置一个相关的判别式
/// checker_tex.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the checker_texture-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { class checker_texture :public texture { public: checker_texture() { } checker_texture(texture* t1, texture* t2); virtual rtvec value(rtvar u, rtvar v, const rtvec& p)const override; private: texture* _even; texture* _odd; }; inline checker_texture::checker_texture(texture * t1, texture * t2) :_even(t1) , _odd(t2) { } rtvec checker_texture::value(rtvar u, rtvar v, const rtvec& p)const { rtvar sines = sin(30 * p.x()) * sin(30 * p.y()) * sin(30 * p.z()); if (sines < 0) return _odd->value(u, v, p); else return _even->value(u, v, p); } }
我们把大球设置为棋盘纹理
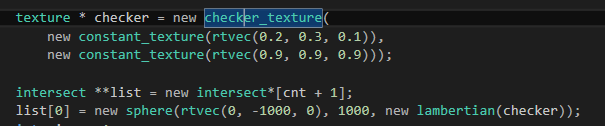
就是开篇图
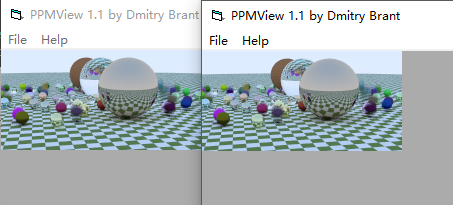
然后,我把判别式中的10改成了30依旧是原图
10(左)30(右)
y = sin(wx + φ)
你可以尝试改动一下φ参数试一下
补充:
使用
使得纹理向屏幕左部偏移了一段距离
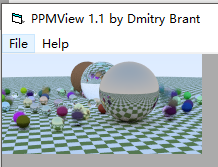
下面是另外一个图:
随机球体生成函数改成

相机参数依旧是之前的

会得到这样一个图

感谢您的阅读,生活愉快~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号