【Ray Tracing in One Weekend 超详解】 光线追踪1-6
新的一年,前来打卡
Preface
回顾上一篇,我们讲述了漫反射材质,也就是平时的磨砂表面。
它一种将入射光经表面随机散射形成的材质,是一种非常普遍的表面形式。
这一篇,我们将来学习镜面反射,或者说是金属材质
镜面在生活中见得也很多,它是一种将入射光经表面按照物理反射规律形成的材质。
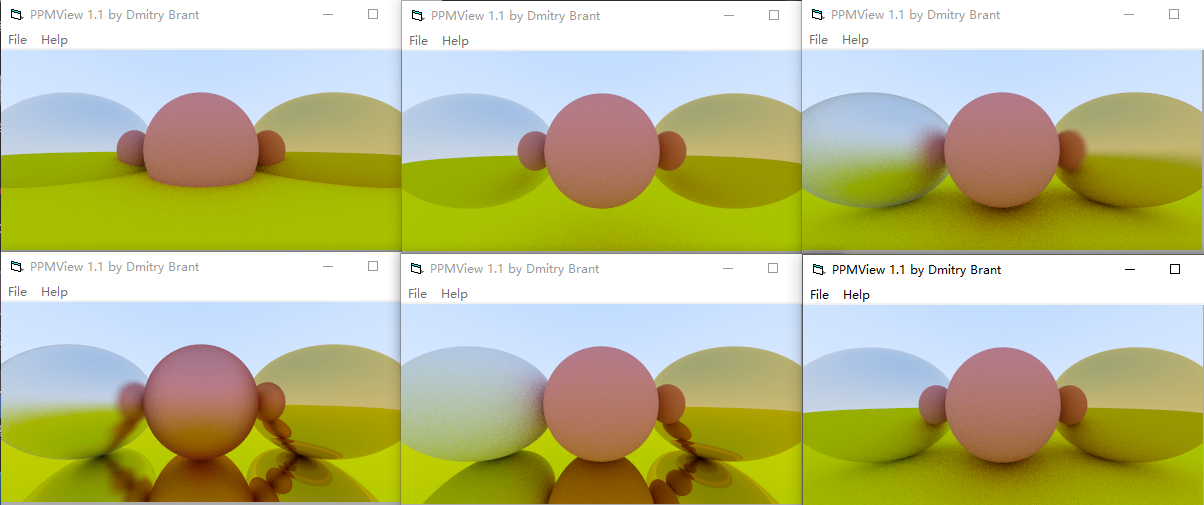
先看效果
Ready
之前我们就写好的
ray.h
intersect.h
intersection.h
sphere.h
camera.h
Chapter8: Metal
之前我们已经写过一个漫反射的材质,可以发现,材质其实就解决两个问题:
1.如何创造反射光或者散射光(吸收转化入射光)
2.如何确定光线强度的衰减量
我们采用类比法:
上一篇中
diffuse表面:1.视线与物体表面产生撞击点p,在p处相切单位圆内随机找一点s,散射光方向即p->s
2.我们上一篇采用的光线强度衰减机制是取半。
这一篇中我们将
metal表面: 1.根据物理反射定律确定入射光对应的反射光的方向
2.强度衰减改为三元组,分别对应rgb三分量的衰减度,且用参数自由确定
那么首先,它们有共同点,我们有必要将其抽象一下
/// material.h // ----------------------------------------------------- // [author] lv // [begin ] 2018.1.1 // [brief ] the material-class for the ray-tracing project // from the 《ray tracing in one week》 // ----------------------------------------------------- #ifndef MATERIAL_H #define MATERIAL_H namespace rt { //abstract basic class class material { public: /* @brief: produce a scattered ray @param: InRay -> Incident light info -> the information of intersect-point(hit-point) attenuation -> when scattered, how much the ray should be attenuated by tis reflectance R scattered -> as we talk, it is a new sight; or it is the scattered ray with the intersect-point @retur: the function calculate a scattered ray or not */ virtual bool scatter(const ray& InRay, const hitInfo& info, rtvec& attenuation, ray& scattered)const = 0; protected: /* @brief: find a random point in unit_sphere */ const rtvec random_unit_sphere()const { rtvec p; do { p = 2.0*rtvec(rtrand01(), rtrand01(), rtrand01()) - rtvec(1, 1, 1); } while (dot(p, p) >= 1.0); return p; } }; } #endif
书上是这样的:

但是取单位圆随机点在两个材质中都有用到,所以,我还是选择把它放在了基类中,可能作者在后面会进行添加,这个不做讨论。
我们继续看一下,如果我们定义了材质,那么我们需要改一些其他的文件内容,将它融入进去
intersect.h中的hitInfo中需要添加

我们现在定义漫反射材质(Diffuse or Lambertian)如下:

/// diffuse.h // ----------------------------------------------------- // [author] lv // [begin ] 2019.1.1 // [brief ] one of the materials // ----------------------------------------------------- #ifndef DIFFUSE_H #define DIFFUSE_H namespace rt { //diffuse material class lambertian : public material { public: lambertian(const rtvec& a) :_albedo(a) { } virtual bool scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const override; protected: rtvec _albedo; }; bool lambertian::scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const { rtvec target = info._p + info._n + random_unit_sphere(); scattered = ray{ info._p, target - info._p }; attenuation = _albedo; return true; } } #endif
scatter函数就是上次主函数里面写的 lerp()
_albedo为衰减三元组,下同,不再赘述
接下来,我们需要了解一下,反射定律;
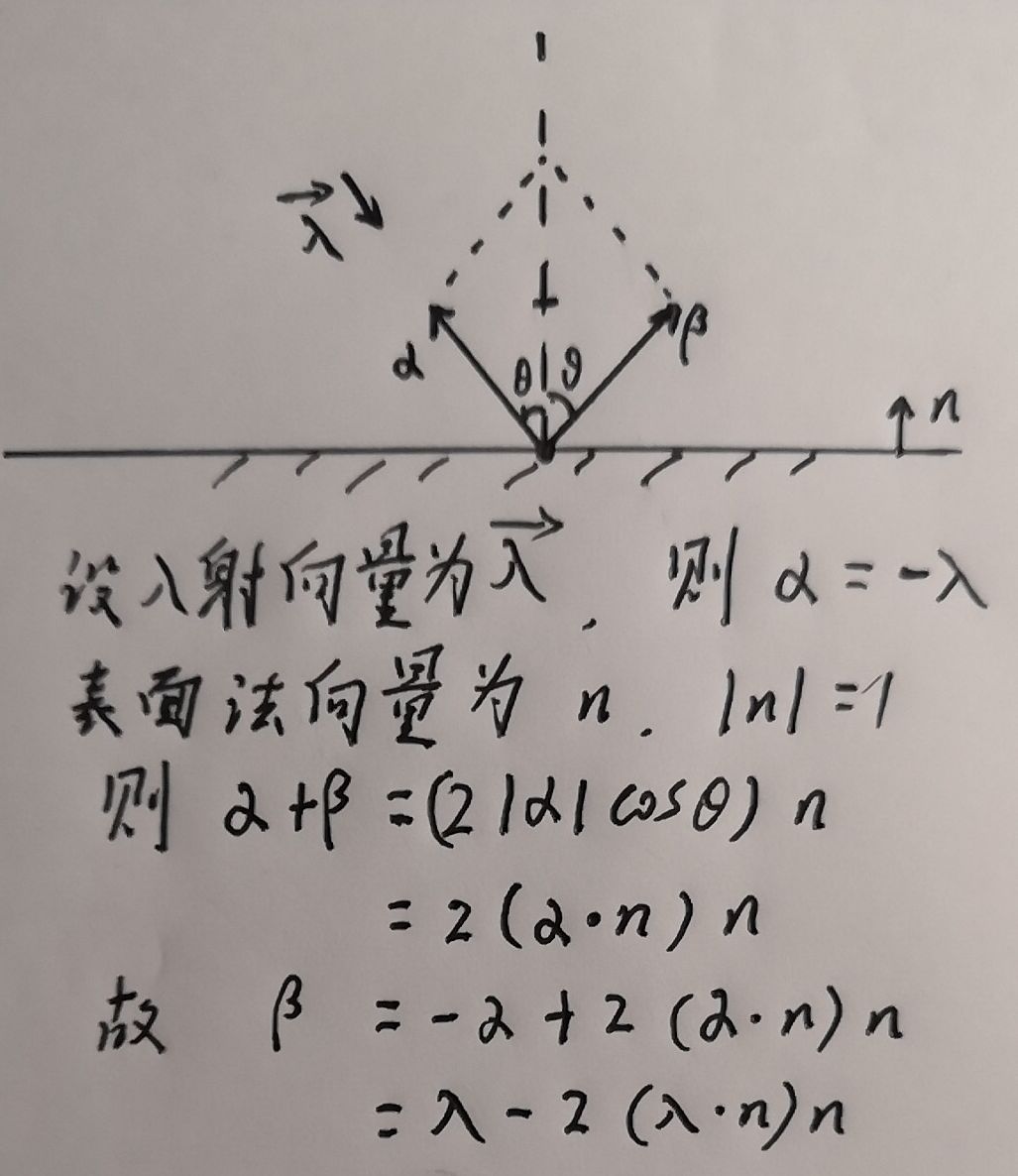
所以,我们的反射函数如下:
inline rtvec reflect(const rtvec& in, const rtvec& n)const { return in - 2 * dot(in, n)*n; }
然后我们就可以写金属材质了

/// metal.h // ----------------------------------------------------- // [author] lv // [begin ] 2018.1.1 // [brief ] one of the materials // ----------------------------------------------------- #ifndef MEATL_H #define METAL_H namespace rt { //metal material class metal :public material { public: metal(const rtvec& a) :_albedo(a) { } virtual bool scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const override; protected: inline rtvec reflect(const rtvec& in, const rtvec& n)const { return in - 2 * dot(in, n)*n; } rtvec _albedo; }; bool metal::scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const { rtvec target = reflect(rIn.direction().ret_unitization(), info._n); scattered = ray{ info._p, target }; attenuation = _albedo; return dot(scattered.direction(), info._n) != 0; } } #endif
这个其实比较简单,就根据反射定律计算出反射向量然后转移视线即可
根据书上的步骤,我们可以先写一个例子了
我们首先写lerp函数
为了避免场景中物体过多,进行非常多次反射降低渲染效率,我们取合适的反射递归深度值作为界限
rtvec lerp(const ray& sight, intersect* world, int depth) { hitInfo info; if (world->hit(sight, (rtvar)0.001, rtInf(), info)) { ray scattered; rtvec attenuation; if (depth < 50 && info.materialp->scatter(sight, info, attenuation, scattered)) return attenuation * lerp(scattered, world, depth + 1); //递归反射,每次反射回退计算rgb的时候进行衰减 else return rtvec(0, 0, 0); } else { rtvec unit_dir = sight.direction().ret_unitization(); rtvar t = 0.5*(unit_dir.y() + 1.); return (1. - t)*rtvec(1., 1., 1.) + t*rtvec(0.5, 0.7, 1.0); } }
我们的main函数:
inline rtvar rtrand01() //https://www.cnblogs.com/lv-anchoret/p/10190092.html { static std::mt19937 mt; static std::uniform_real_distribution<rtvar> rtrand; return rtrand(mt); }
main:
stds ofstream file("graph8-1.ppm"); size_t W = 400, H = 200, sample = 100; if (file.is_open()) { file << "P3\n" << W << " " << H << "\n255\n" << stds endl; size_t sphereCnt = 4; intersect** list = new intersect*[sphereCnt]; list[0] = new sphere(rtvec(0, 0, -1), 0.5, new lambertian(rtvec(0.8,0.3,0.3))); list[1] = new sphere(rtvec(0, -100.5, -1), 100, new lambertian(rtvec(0.8, 0.8, 0.))); list[3] = new sphere(rtvec(-1, 0, -1), 0.5, new metal(rtvec(0.8, 0.8, 0.8))); list[2] = new sphere(rtvec(1, 0, -1), 0.5, new metal(rtvec(0.8, 0.6, 0.2))); intersect* world = new intersections(list, sphereCnt); camera cma; for (int y = H - 1; y >= 0; --y) for (int x = 0; x < W; ++x) { rtvec color; for (int cnt = 0; cnt < sample; ++cnt) { lvgm::vec2<rtvar> para{ (rtrand01() + x) / W, (rtrand01() + y) / H }; color += lerp(cma.get_ray(para), world, 0); } color /= sample; color = rtvec(sqrt(color.r()), sqrt(color.g()), sqrt(color.b())); //gamma 校正,上一篇讲过 int r = int(255.99 * color.r()); int g = int(255.99 * color.g()); int b = int(255.99 * color.b()); file << r << " " << g << " " << b << stds endl; } file.close(); if (list[0])delete list[0]; if (list[1])delete list[1]; if (list[2])delete list[2]; if (list[3])delete list[3]; if (list)delete[] list; if (world)delete world; stds cout << "complished" << stds endl; } else stds cerr << "open file error" << stds endl;
上述的sphere对象增加了材质,所以我们需要为sphere-class做一些适当的补充

/// sphere.h // ----------------------------------------------------- // [author] lv // [begin ] 2018.1.1 // [brief ] the sphere-class for the ray-tracing project // from the 《ray tracing in one week》 // ----------------------------------------------------- #ifndef SPHERE_H #define SPHERE_H namespace rt { class sphere :public intersect { public: sphere() { } /* @para1: 球心坐标 @para2: 球半径 @para3: 材质 */ sphere(const rtvec& h, rtvar r, material* ma) :_heart(h), _radius(r), _materialp(ma) { } ~sphere() { if (_materialp) delete _materialp; } virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& rec)const override; inline const rtvar r()const { return _radius; } inline const rtvec& heart()const { return _heart; } inline rtvar& r() { return _radius; } inline rtvec& heart() { return _heart; } private: rtvec _heart; rtvar _radius; material* _materialp; }; bool sphere::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& rec)const { rtvec trace = sight.origin() - _heart; rtvar a = dot(sight.direction(), sight.direction()); rtvar b = 2.0 * dot(trace, sight.direction()); rtvar c = dot(trace, trace) - _radius * _radius; rtvar delt = b*b - 4.0*a*c; if (delt > 0) { rec.materialp = _materialp; rtvar x = (-b - sqrt(delt)) / (2.0*a); if (x < t_max && x > t_min) { rec._t = x; rec._p = sight.go(rec._t); rec._n = (rec._p - _heart) / _radius; return true; } x = (-b + sqrt(delt)) / (2.0*a); if (x < t_max && x > t_min) { rec._t = x; rec._p = sight.go(x); rec._n = (rec._p - _heart) / _radius; return true; } } return false; } } #endif
我们创建了四个球
中间heart:(0,0,1) r:0.5
下面heart:(0,-100.5,-1) r:100
左边heart:(-1,0,-1) r:0.5
右边heart:(1,0,-1) r:0.5
左右为镜面,中间和下面是磨砂

回顾我们的标准屏幕坐标系:coor 1.1
中间球的球心 ,距上边界为1,距下边界为1,距左边界为2,距右边界为2
所以,绿色球(heart(0,-100.5,-1), r:100)超出屏幕底部0.5,意思是和三个球的底部是契合的,所以,它们之间有三个接触的阴影
而左右两个球中的画面均为镜面反射,并不是透明,中间球两边的小球是在旁边球面的球面镜像
我们可以测验下,比如把绿球的半径改为100.3,即

则是这样的:

现在总该相信,绿球的上边界并不是图中的绿色横线,那些都是左右球镜面反射的镜像。
你也可以把绿球的半径改为99.7

三个球的底部和绿球并没有接触阴影,且球镜面镜像中绿色横线边界有所降低
如果没有明白,我们来屡一下流程再继续往下走:
流程
1.我们先创建几个sphere,每个都需要有球心、半径、rgb衰减三元组和材质
2.视线扫描屏幕
3.lerp计算
1)当前视线和场景中所有的物体求表面交点,求最近点,顺便把交点的信息都记录下来,包括位置,表面法线和该点所在的sphere中的材质信息
2)如果有交点:根据交点的材质,计算反射或散射向量,顺便把材质中的衰减三元组信息通过参数传出来,然后返回rgb的时候进行rgb分量衰减,根据求取的scattered-ray,进行视线转移(视点转换);如果没有交点了,那么返回该位置对应的背景插值颜色
4.采样
5.gamma校正
6.输出屏幕中该点的信息
那么,我们还是来关注下这里面的一些个有趣的事情,好像有一个叫衰减三元组的,使用计算反射后的光线的rgb乘以三元组进行分量衰减,那么,如果衰减三元组为(1,1,1),那么意思就是保持原值,未损失,那么我们把场景中所有的sphere中的衰减三元组均改为(1,1,1),会是什么样子的呢?
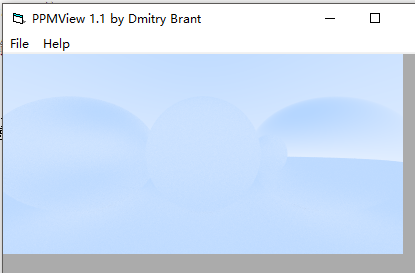
非常不明显,尤其是中间和下面,基本看不到了,右边还算有些轮廓
因为,漫反射材质散射方向随机,所以如果不把散射光进行逐步衰减的话,基本就是周围背景色,所以,漫反射材质很容易融入坏境
而镜面是严格的物理反射规律,所以上半部分会用更上面的光代替,下面的会用下面的光代替,所以还是有一些色差的
左面的部分还加了镜面模糊效果的,镜面模糊下面讲
镜面模糊其实就是 镜面 + 模糊系数*漫反射
漫反射实现原理是根据随机化s点,所以模糊镜面实现公式即为:
模糊镜面反射 = 镜面反射 + 模糊系数 * 单位球随机点漫反射
引用书中一张图:
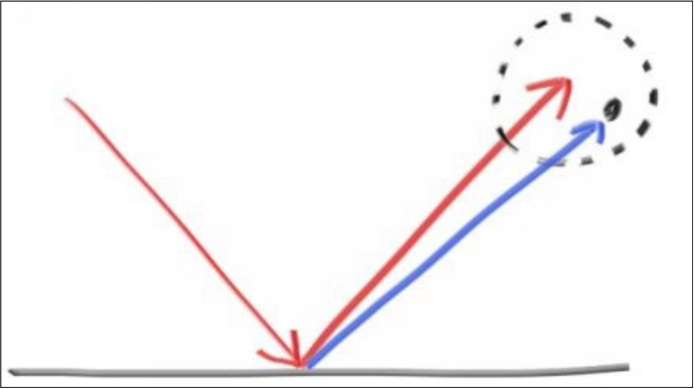
模糊原理就和漫反射原理差不多
/// metal.h // ----------------------------------------------------- // [author] lv // [begin ] 2018.1.1 // [brief ] one of the materials // ----------------------------------------------------- #ifndef MEATL_H #define METAL_H namespace rt { //metal material class metal :public material { public: metal(const rtvec& a, const rtvar f = 0.) :_albedo(a) { if (f < 1 && f >= 0)_fuzz = f; else _fuzz = 1; } virtual bool scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const override; protected: inline rtvec reflect(const rtvec& in, const rtvec& n)const { return in - 2 * dot(in, n)*n; } rtvec _albedo; rtvar _fuzz; }; bool metal::scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const { rtvec target = reflect(rIn.direction().ret_unitization(), info._n); scattered = ray{ info._p, target + _fuzz * random_unit_sphere() }; attenuation = _albedo; return dot(scattered.direction(), info._n) != 0; } } #endif
所以我们在main中创建sphere时,还要指定模糊系数,默认为0(不模糊)
我们来测试下模糊系数,如果左右两个镜面的模糊系数分别为0.7和0.2的话,是这个样子的:

如果只把右边和下边改为镜面,那么就很有意思了:

最后一张,全镜面,左球和中球模糊

是不是感觉非常有意思
遗留工程问题
一个基类material,里面一个纯虚函数scatter
两个子类,metal和Lambertian
两个子类的类声明放在头文件中,将scatter函数实现放在源文件中
会有一个子类的scatter无法解析
感谢您的阅读,生活愉快~


