【Ray Tracing in One Weekend 超详解】 光线追踪1-5
一天一篇,今天来学习第7章 (散射)漫反射材质
Chapter7: Diffuse Materials
Preface
从这一章开始,我们将通过光线追踪制作一些逼真的材质。
我们将从漫射(磨砂)材料开始。
先看效果:

正文
不发光的漫射物体仅仅呈现其周围的颜色,但是它们用它们自己的固有颜色来调和这些色彩。
从漫反射表面反射的光方向是随机的,比如:如果我们将三条光线发送到一个漫反射表面,它们将各自具有不同的随机行为:
引用书上的图:

diagram 7-1
它们也可能被吸收而不是被反射。 表面越暗,光线越可能被吸收。 (这就是为什么它是黑的!)
任何随机化方向的算法都会产生看起来很粗糙的表面。 最简单的方法之一是理想的漫反射表面。
原文还提到了Lambertian发射面
我们来看一下,如何实现上述功能
图说一切:

diagram 7-2
图解
先简述一下各个原件:左黄球是以eye为中心的一个单位圆,右黄球是一个和左黄球一样的圆,至于怎么生成的,后续说
左黄球上有两个随机点,蓝紫色的s1,红紫色的s2,对应于右黄球上为s1' 和s2'
红色为视线;深绿色为反射线;三个黑球为漫反射球体,黑色只是用颜色来区分各个原件的功能,并不是黑色的漫反射球(画完才发现,黑球都把光线吸收了。。。。==!)
实现过程
步骤一:从eye发出一条视线,交球面于p点,之后我们确定随机反射方向
将右边的黄色圆部分放大:
引用书中一张图:
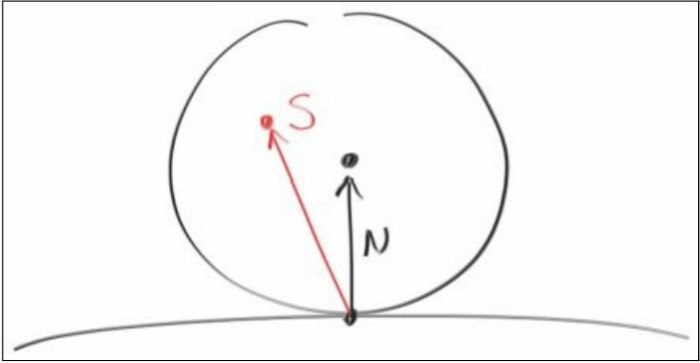
diagram 7-3
n为P点的单位法向量,方向向外,下面那个点是碰撞点P,找一个和点P相切的单位圆
而这个圆的圆心o的位置就等于p+n(p : eye->P),因为我们的原点就是eye,所以根据向量就可以得出位置信息
基于eye的向量和位置体系,其实方便了我们利用向量运算代替位置运算,更直观。这个自己理解下就好,不是重点。
步骤二:then, we pick a random point s from the unit randius sphere.
当我们找到这个s点之后,我们将沿着p->s的方向进行反射,但是我们如何找这个random point呢?
这个时候我们就需要用到我们的diagram 7-2了,回去看一眼那个蓝紫色点s1,做一个平行四边形,对应到s1',他们是等价的(向量只用方向和大小进行定义,不规定起始位置,所以我们能说它们等价)。
我们先在原点单位球中找一个随机点,构成一个eye->s的向量s1,然后,将s1的起点移动到o处,即s1',也就是说s1'就是我们要求的随机点,因为直接求随机点s1'的位置并不好求,所以,只能这样,其实想是很好想,但是要描述清楚就应该是这么描述。
步骤三:最后我们得到反射线的方向dir = s1' - p,s1' = o + s1, o = p + n
然后,我们来求s1:
#include <random> #define stds std:: using namespace rt; stds mt19937 mt; stds uniform_real_distribution<rtvar> rtrand; const rtvec random_unit_sphere() { rtvec p; do { p = 2.0*rtvec(rtrand(mt), rtrand(mt), rtrand(mt)) - rtvec(1, 1, 1); } while (dot(p, p) >= 1.0); //rejection method return p; }
关于随机数生成,在上一篇讲过了,应该是靠后讲的
rtrand生成的是0~1的随机数,然后乘以2再减去1,得到的p的每一个分量均位于-1~1,其实它的范围是一个正方体,而我们要求的是球内随机点。
所以我们采用书中所述的rejection方法,拒绝非法点:如果基于原点eye找一个随机点(x,y,z)
如果x*x+y*y+z*z>=1,那么它不符合我们的需要,我们重新找。

最后,我们通过上面的代码就得到了一个球内随机点。
上述就是diagram 7-2中基于蓝紫色点进行反射的深绿色光线的反射过程
当然,还有基于红紫色的反射线,前半部分就和上面一样,所以也没有画平行四边形,关于后续反射
步骤四:将当前碰撞点P作为eye,以反射方向向量dir为视线方向进行步骤一
直到没有碰撞,为止
而且,光线没经过一次反射强度就会衰减,我们也是这么做的,我们采用的是每反射一次,衰减一半。
#define LOWPRECISION #include <fstream> #include "intersect.h" #include "sphere.h" #include "intersections.h" #include "camera.h" #include <random> #define stds std:: using namespace rt; stds mt19937 mt; stds uniform_real_distribution<rtvar> rtrand; const rtvec random_unit_sphere() { rtvec p; do { p = 2.0*rtvec(rtrand(mt), rtrand(mt), rtrand(mt)) - rtvec(1, 1, 1); } while (dot(p, p) >= 1.0); return p; } rtvec lerp(const ray& sight, const intersect* world) { hitInfo rec; if (world->hit(sight, 0., intersect::inf(), rec)) //如果没有有效碰撞点 { rtvec target = rec._p + rec._n + random_unit_sphere(); //随机点s的最后位置 return 0.5*lerp(ray{ rec._p,target - rec._p }, world); //强度衰减,新建eye继续发射视线 } else { rtvec dirUnit = sight.direction().ret_unitization(); rtvar t = 0.5*(dirUnit.y() + 1.); return (1. - t)*rtvec(1., 1., 1.) + t*rtvec(0.5, 0.7, 1.0); } } void build_7_1() { stds ofstream file("graph7-1.ppm"); size_t W = 400, H = 200, sample = 100; if (file.is_open()) { file << "P3\n" << W << " " << H << "\n255\n" << stds endl; intersect** list = new intersect*[2]; list[0] = new sphere(rtvec(0, 0, -1), 0.5); list[1] = new sphere(rtvec(0, -100.5, -1), 100); intersect* world = new intersections(list, 2); camera cma; for (int y = H - 1; y >= 0; --y) for (int x = 0; x < W; ++x) { rtvec color; for (int cnt = 0; cnt < sample; ++cnt) { lvgm::vec2<rtvar> para{ (rtrand(mt) + x) / W, (rtrand(mt) + y) / H }; color += lerp(cma.get_ray(para), world); } color /= sample; int r = int(255.99 * color.r()); int g = int(255.99 * color.g()); int b = int(255.99 * color.b()); file << r << " " << g << " " << b << stds endl; } stds cout << "complished" << stds endl; file.close(); if (list[0])delete list[0]; if (list[1])delete list[1]; if (list)delete[] list; if (world)delete world; } else stds cerr << "open file error" << stds endl; } int main() { build_7_1(); }
效果图如下:

注意球体下的阴影。 这张照片非常暗,但是我们的球体在光线每次反射时只吸收了一半的能量,因此它们是50%的反射器。
在现实生活中, 这些球体应该是浅灰色的。 其原因在于几乎所有图像观看者都假设图像是“伽马校正的”,这意味着这些0到1的值在被存储为字节之前做了一些变换。这种做法有很多好处,但就我们的目的而言,今天不讲这个,了解即可。
如果我们对我们日常的视觉做一个近似,我们可以使用“gamma 2”,即只是简单的平方根:
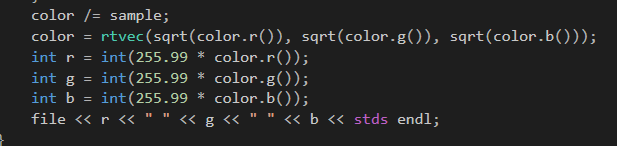
这样就会得到下图:

看起来更好些。
感谢您的阅读,生活愉快~


