java 算法实现

（1）时间频度：一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

（2）时间复杂度：算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。去掉常数项+去低阶项+去掉最高阶系数

常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2*n)＜Ο(n!)

1.1 选择 排序

选择排序算法也是比较简单的排序算法,其思路比较直观。选择排序算法在每一步中选取最小值来重新排列,从而达到排序的目的。   选择排序算法通过选择和交换来实现排序,其排序流程如下:

1.首先从原始数组中选择最小的1个数据,将其和位于第1个位置的数据交换。
2.接着从剩下的 n-1 个数据中选择次小的 1 个数据,将其和第2个位置的数据交换。
3.然后不断重复上述过程,直到最后两个数据完成交换。至此,便完成了对原始数组的从小到大的排序。

public class Xzz {
  public static void sortXz(int[] arr){
    int d,e;
    for(int i=0;i<arr.length-1;i++){
      d=i;
      for(int j=i+1;j<arr.length;j++){
        if(arr[j]<arr[d]){  // 若剩余 n-(i+1) 个数据中有小于 a[i]的，则记录该元素下标
          d=j;
        }
        if(d!=i){
          e = arr[i];
          arr[i] = arr[d];
          arr[d] = e;
        } } } }
  public static void main(String[] args) {
    int[] a=new int[20];
    Random random=new Random();
    for(int i=0;i<20;i++){
      a[i]=random.nextInt(100);
    }
  Xzz.sortXz(a);
    for(int i=0;i<a.length;i++){
      System.out.printf("%d ",a[i]);
    }
  }
}

1.2 插入排序

1.将一组数据分成两组，分别为有序组、无序组（一般将数据第一个元素视为有序组，剩余为无序组）。
2.取出无序组第一个元素，按从后向前的顺序，与有序组的元素逐个比较，插入到有序组合适位置。
3.重复步骤 2， 直至无序组元素为空。

插入排序对小规模数据或基本有序数据比较有效。数据有序程度越高，越有效

public class Cr {
  public static void InsertSort(int[] arr) {
    int k=0,j ;
    for(int i=1;i<arr.length;i++){
      k=arr[i];              // 从无序组取出第一个元素
      j=i-1;                  // i-1 即为有序组最后一个元素（与待插入元素相邻）的下标
      // 按从后向前的顺序，将待插入元素与有序组元素逐个比较
      while (j>=0&&k<arr[j]){
        arr[j+1]=arr[j];    // 若不是合适位置，有序组元素向后移动
        j--;
      }
      arr[j+1]=k;          // 找到合适位置，将元素插入
    }
  }
  public static void main(String[] args) {
    int[] a=new int[20];
    Random random=new Random();
    for(int i=0;i<20;i++){
      a[i]=random.nextInt(100);
    }
    Cr.InsertSort(a);
    for(int i=0;i<a.length;i++){
      System.out.printf("%d ",a[i]);
    }
  }
}
​

1.3 希尔排序（shell排序/缩小增量排序）

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的），对每个子序列进行直接插入排序。然后缩减增量对子序列进行排序…，直至增量为 1 时，将整个元素序列变为有序。

希尔排序适用于大规模且无序的数据

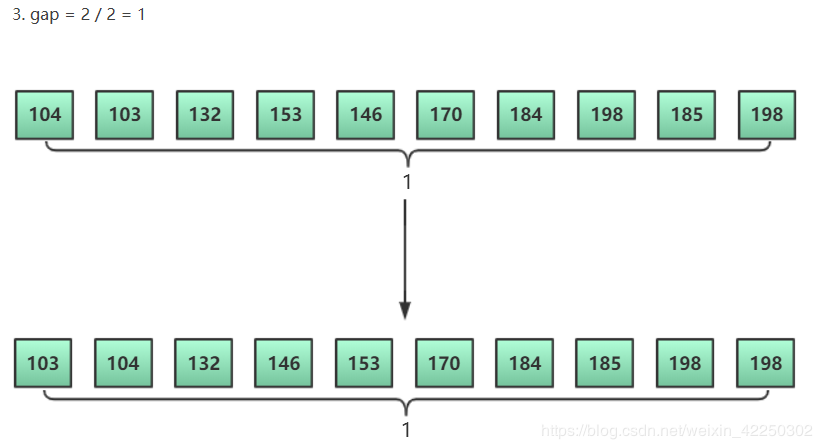
1.假设共有 n 个元素，第一次取增量 gap = n / 2，对 gap 个元素序列进行插入排序
2.取 gap = gap / 2，对 gap 个元素序列进行插入排序
3.重复步骤 2，直至 gap = 1，将整个元素序列变为有序

public class XXee {
  static final int SIZE = 20;
  public static void shellSort(int[] array) {
    int j, temp, k = 0;
    for (int gap = array.length / 2; gap >= 1; gap /= 2) {
      // 对子序列进行插入排序
      for (int i = gap; i < array.length; i++) {
        temp = array[i];            // 取无序组第一个元素，此元素即为待插入元素
        j = i - gap;                // i-gap 为有序组最后一个元素
        // 按从后向前的顺序，将待插入元素与有序组元素逐个比较
        while (j >= 0 && temp < array[j]) {
          array[j+gap] = array[j];// 若不是合适位置，有序组元素向后移动
          j -= gap;
        }
        array[j+gap] = temp;        // 找到合适位置，将元素插入
      }
      System.out.print("第" + ++k + "步排序结果：");
      Arrays.stream(array).mapToObj(item -> item + " ").forEach(System.out::print);
      System.out.println();
    }
  }
  public static void main(String[] args) {
    int[] array = new int[SIZE];
​
    System.out.println("排序前的数组为：");
    for (int i = 0; i < SIZE; i++) {
      // 产生 100~199 之间的随机数
      array[i] = (int) (100 + Math.random() * 100);
      System.out.printf("%d ", array[i]);
      if ((i + 1) % 10 == 0)
        System.out.println();
    }
​
    shellSort(array);
    System.out.println("排序后的数组为：");
    for (int i = 0; i < array.length; i++) {
      System.out.printf("%d ", array[i]);
      if ((i + 1) % 10 == 0)
        System.out.println();
    }
  }
}

1.4 快速排序

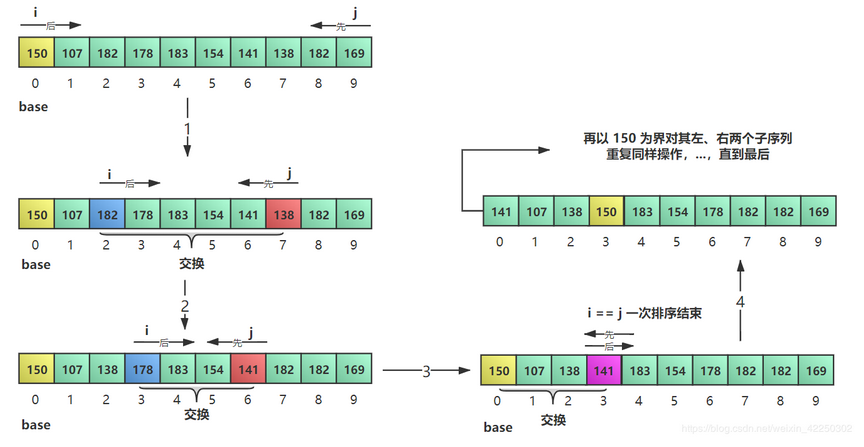
假设有一个由若干数据组成的序列，

取第一个数据为基准数据 base，指针 i 指向第一个数据，指针 j 指向最后一个数据；
当 i < j 时：先递减 j，从后向前搜索小于 base 的数据，再递增 i ，从前向后搜索大于 base 的数据，若找到，则交换；继续递减 j，递增 i 进行同样的操作，直至 i == j
当 i == j 时：交换 base 和 array[i]，则 base 左侧的数据都小于 base，base 右侧的数据都大于base，此时一次排序结束
以 base 为界限将数据分成两个子序列，对子序列进行同样的操作，…，直到整个序列有序

array[10] = { 150 107 182 178 183 154 141 138 182 169 } 

public class QuickSortDemo {
  static final int SIZE = 20;
  static int k = 0;
​
  public static void quickSort(int[] array, int left, int right) {
    // 数组长度为 0 或 1 时直接退出
    if (array == null || left > right || (array.length - 1 <= 0))
      return;
​
    int base = array[left]; // base：基准数据
    int i = left, j = right;// 让 i 指向数据最左侧，让 j 指向数据最左侧
    int temp;
    while (i != j) {
      // 从右向左搜寻小于 base 的数据
      while (array[j] >= base && i < j)
        j--;
      // 从左向右搜寻大于 base 的数据
      while (array[i] <= base && i < j)
        i++;
​
      // 交换搜寻到的数据
      if (i < j) {
        temp = array[i];
        array[i] = array[j];
        array[j] = temp;
      }
    }
​
    // 将基准数放到中间的位置（基准数归位）
    array[left] = array[i];
    array[i] = base;
        /*temp = array[i];
        array[i] = array[left];
        array[left] = temp;*/
    // 一次排序结束，此时 base 左侧的数据全小于 base，右侧的数据全大于base
​
    quickSort(array, left, i - 1); // 快排 base 左侧数据
    quickSort(array, i + 1, right);// 快排 base 右侧数据
  }
​
  public static void main(String[] args) {
    int[] array = new int[SIZE];
​
    System.out.println("排序前的数组为：");
    for (int i = 0; i < SIZE; i++) {
      // 产生 100~199 之间的随机数
      array[i] = (int) (100 + Math.random() * 100);
      System.out.printf("%d ", array[i]);
    }
​
    quickSort(array, 0, array.length - 1);
    System.out.println("\n排序后的数组为：");
    for (int i = 0; i < SIZE; i++) {
      System.out.printf("%d ", array[i]);
    }
  }
​
}

1.5 堆排序

堆排序

　　堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

大顶堆：非叶结点的数据 >= 其左、右子结点的数据。
小顶堆：非叶结点的数据 <= 其左、右子结点的数据。

public class HeapSortDemo {
    static final int SIZE = 20;
    static int k = 0;
​
    public static void heapSort(int[] array) {
        // 数组长度为 0 或 1 时直接退出
        if (array == null || (array.length - 1 <= 0))
            return;
​
         //1.构建大顶堆
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            //从最后一个非叶结点开始，从下到上，从右到左调整堆结构
            adjustHeap(array, i, array.length);
        }
​
        int temp;
        for (int i = array.length - 1; i > 0; i--) {
            // 交换堆顶元素与末尾元素
            temp = array[i];
            array[i] = array[0];
            array[0] = temp;
​
            // 除末尾元素外，继续调整剩余元素
            adjustHeap(array, 0, i);
        }
    }
​
    public static void adjustHeap(int[] array, int i, int length) {
        int temp = array[i];//先取出当前元素i
        for (int j = i * 2 + 1; j < length; j = j * 2 + 1) {//从i结点的左子结点开始，也就是2i+1处开始
            if (j + 1 < length && array[j] < array[j + 1])//如果左子结点小于右子结点，j指向右子结点
                j++;
            if (array[j] > temp) {//如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
                array[i] = array[j];
                i = j; // 令 i 指向被改变的子树
            } else {
                break;
            }
            array[i] = temp;//将temp值放到最终的位置
        }
    }
​
    public static void main(String[] args) {
        int[] array = new int[SIZE];
​
        System.out.println("排序前的数组为：");
        for (int i = 0; i < SIZE; i++) {
            // 产生 100~199 之间的随机数
            array[i] = (int) (100 + Math.random() * 100);
            System.out.printf("%d ", array[i]);
        }
​
        heapSort(array);
        System.out.println("\n排序后的数组为：");
        Arrays.stream(array).mapToObj(e -> e + " ").forEach(System.out::print);
    }
}
​

1.6 归并排序

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

public class MergeSortDemo {
    static final int SIZE = 20;
    public static void mergeSort(int[] array, int low, int high, int[] temp) {
        if (low < high) {
            int mid = (low + high) / 2;
            mergeSort(array, low, mid, temp);
            mergeSort(array, mid + 1, high, temp);
            merge(array, low, mid, high, temp);
        }
    }
​
    private static void merge(int[] array, int low, int mid, int high, int[] temp) {
        // j 为左边序列起始索引，k 为右边序列起始索引
        int i = 0, j = low, k = mid + 1;
​
        // 将两个序列中较小值移入 temp
        while (j <= mid && k <= high) {
            if (array[j] < array[k])
                temp[i++] = array[j++];
            else
                temp[i++] = array[k++];
        }
​
        // 将左边序列剩余元素移入 temp
        while (j <= mid)
            temp[i++] = array[j++];
        // 将右边序列剩余元素移入 temp
        while (k <= high)
            temp[i++] = array[k++];
        // 用 temp 数组覆盖 array 数组
        for (int l = 0; l < i; l++) {
            array[low + l] = temp[l];
        }
    }
​
    public static void main(String[] args) {
        int[] array = new int[SIZE];
        int[] temp = new int[array.length];
​
        System.out.println("排序前的数组为：");
        for (int i = 0; i < SIZE; i++) {
            // 产生 100~199 之间的随机数
            array[i] = (int) (100 + Math.random() * 100);
            System.out.printf("%d ", array[i]);
        }
​
        mergeSort(array, 0, array.length - 1, temp);
        System.out.printf("\n排序后的数组为：\n%s\n", Arrays.toString(array));
    }
}

1.7 冒泡排序

冒泡排序的基本思想是，对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序

public class Mb {
  public static void main(String[] args) {
    int[] a=new int[]{1,9,5,56,23};
      int k=0;
    for(int i=0;i<a.length-1;i++){
      for(int j=0;j<a.length-1-i;j++){
         if(a[j]>a[j+1]){
          k=a[j];
          a[j]=a[j+1];
          a[j+1]=k;
        }
      }
    }
    for(int i=0;i<a.length;i++){
​
      System.out.println(a[i]);
    }
  }
}