判断素数

素数又称质数。所谓素数是指除了 1 和它本身以外，不能被任何整数整除的数，例如17就是素数，因为它不能被 2~16 的任一整数整除。

思路1)：因此判断一个整数m是否是素数，只需把 m 被 2 ~ m-1 之间的每一个整数去除，如果都不能被整除，那么 m 就是一个素数。

思路2)：另外判断方法还可以简化。m 不必被 2 ~ m-1 之间的每一个整数去除，只需被 2 ~ 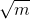 之间的每一个整数去除就可以了。如果 m 不能被 2 ~  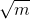间任一整数整除，m 必定是素数。例如判别 17 是是否为素数，只需使 17 被 2~4 之间的每一个整数去除，由于都不能整除，可以判定 17 是素数。

原因：因为如果 m 能被 2 ~ m-1 之间任一整数整除，其二个因子必定有一个小于或等于 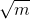，另一个大于或等于 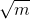。例如 16 能被 2、4、8 整除，16=2*8，2 小于 4，8 大于 4，16=4*4，4=√16，因此只需判定在 2~4 之间有无因子即可。

两种思路的代码请看解析。

思路1) 的代码：

#include <stdio.h>

int main(){
    int a=0;  // 素数的个数
    int num=0;  // 输入的整数

    printf("输入一个整数：");
    scanf("%d",&num);

    for(int i=2;i<num;i++){
        if(num%i==0){
            a++;  // 素数个数加1
        }
    }

    if(a==0){
        printf("%d是素数。\n", num);
    }else{
        printf("%d不是素数。\n", num);
    }

    return 0;
}

　　思路2)的代码：

#include <stdio.h>
#include <math.h>
void main(){
    int m;  // 输入的整数 
    int i;  // 循环次数
    int k;  // m 的平方根 

    printf("输入一个整数：");
    scanf("%d",&m);

    // 求平方根，注意sqrt()的参数为 double 类型，这里要强制转换m的类型 
    k=(int)sqrt( (double)m );
    for(i=2;i<=k;i++)
        if(m%i==0)
            break;

    // 如果完成所有循环，那么m为素数
    // 注意最后一次循环，会执行i++，此时 i=k+1，所以有i>k 
    if(i>k)
        printf("%d是素数。\n",m);
    else
        printf("%d不是素数。\n",m);

    return 0;
}

　　

两段代码的输出结果相同。

第一次运行结果：
输入一个整数：1
1是素数。

第二次运行结果：
输入一个整数：97
97是素数。

第三次运行结果：
输入一个整数：10
10不是素数。