洛谷3934：Nephren Ruq Insania——题解

https://www.luogu.org/problemnew/show/P3934

题面自己读吧（滑稽。

看到这道题就能够想到BZOJ4869：[SHOI2017]相逢是问候我们曾经用过的哲学扩展欧拉定理。

（咦什么时候这个东西都普及到noip了好方啊）

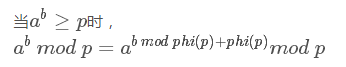
也就是说，不论询问的区间[l,r]长度有多大，实际上我们暴力算只需要logp次模数就变成了1之后的询问就不需要担心了。

区间修改可以线段树/树状数组来干。

敲完发现是70pts，很难受。

有没有发现这个公式前面有一个前提？其实，当a^b<p的时候，a的指数就不应当加phi(p)了，这也就是错的原因。

我们当然可以每次传递当前的b是否曾经对phi(p)取过模来决定是否加phi(p)，经过多次修改之后终于AC了……

PS：请注意我们运算的时候很可能出现x^0%x=1这种情况，而显然我们希望的答案应当为0（虽然我并不知道为什么），所以需要特判之。

#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+5;
const int M=2e7+5;
inline int read(){
    int X=0,w=0;char ch=0;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
bool ok[N];
ll qpow(ll k,ll n,int p,int l){
    ll res=1;
    while(n){
        if(n&1){
            res*=k;
            if(res>=p)ok[l]=1,res%=p;
        }
        k*=k;n>>=1;
        if(k>=p)ok[l]=1,k%=p;
    }
    return res;
}
int n,m;
int su[M],he[M],phi[M],tot;
ll tr[N*4],lz[N*4],b[N];
void Euler(int n){
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!he[i])su[++tot]=i,phi[i]=i-1;
        for(int j=1;j<=tot;j++){
            if(i*su[j]>n)break;
            he[i*su[j]]=1;
            if(i%su[j]==0){
                phi[i*su[j]]=phi[i]*su[j];
                break;
            }else phi[i*su[j]]=phi[i]*phi[su[j]];
        }
    }
}
inline void push(int a,int l,int r){
    if(!lz[a])return;
    int mid=(l+r)>>1;
    lz[a<<1]+=lz[a];lz[a<<1|1]+=lz[a];
    if(l==mid)tr[a<<1]+=lz[a];
    if(mid+1==r)tr[a<<1|1]+=lz[a];
    lz[a]=0;
}
void build(int a,int l,int r){
    if(l==r){
        tr[a]=b[l];return;
    }
    int mid=(l+r)>>1;
    build(a<<1,l,mid);build(a<<1|1,mid+1,r);
}
void add(int a,int l,int r,int l1,int r1,int x){
    if(r<l1||r1<l)return;
    if(l1<=l&&r<=r1){
        lz[a]+=x;
        if(l==r)tr[a]+=x;
        return;
    }
    push(a,l,r);
    int mid=(l+r)>>1;
    add(a<<1,l,mid,l1,r1,x);add(a<<1|1,mid+1,r,l1,r1,x);
}
ll ask(int a,int l,int r,int k){
    if(l==r)return tr[a];
    push(a,l,r);
    int mid=(l+r)>>1;
    if(k<=mid)return ask(a<<1,l,mid,k);
    else return ask(a<<1|1,mid+1,r,k);
}
ll query(int l,int r,int p){
    ok[l]=0;
    ll ans=ask(1,1,n,l);
    if(ans>=p)ok[l]=1;
    if(ans%p==0)return 0;
    if(p==1)return 1;
    ans%=p;
    if(l==r)return ans;
    ll tmp=query(l+1,r,phi[p]);
    return qpow(ans,tmp+(ok[l+1]?phi[p]:0),p,l);
}
int main(){
    Euler(2e7);
    n=read(),m=read();
    for(int i=1;i<=n;i++)b[i]=read();
    build(1,1,n);
    for(int i=1;i<=m;i++){
        int op=read();
        if(op==1){
            int l=read(),r=read(),x=read();
            add(1,1,n,l,r,x);
        }else{
            int l=read(),r=read(),p=read();
            printf("%lld\n",query(l,r,p));
        }
    }
    return 0;
}

当然还有另外一种（正解）的做法。

考虑到假设我们暴力枚举模拟前几次操作之后，往后的操作基本都是大于phi(p)的，而没有加phi(p)的只可能是前面几项。

故暴力处理前面几项即可，常数显然要比上面的方法要大很多。

#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+5;
const int M=2e7+5;
inline int read(){
    int X=0,w=0;char ch=0;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
int qpow(int k,ll n,int p){
    int res=1;
    while(n){
        if(n&1)res=(ll)res*k%p;
        k=(ll)k*k%p;n>>=1;
    }
    return res;
}
int n,m,tag[N];
int su[M],he[M],phi[M],tot;
ll tr[N*4],lz[N*4],b[N];
void Euler(int n){
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!he[i])su[++tot]=i,phi[i]=i-1;
        for(int j=1;j<=tot;j++){
            if(i*su[j]>n)break;
            he[i*su[j]]=1;
            if(i%su[j]==0){
                phi[i*su[j]]=phi[i]*su[j];
                break;
            }else phi[i*su[j]]=phi[i]*phi[su[j]];
        }
    }
}
inline void push(int a,int l,int r){
    if(!lz[a])return;
    int mid=(l+r)>>1;
    lz[a<<1]+=lz[a];lz[a<<1|1]+=lz[a];
    if(l==mid)tr[a<<1]+=lz[a];
    if(mid+1==r)tr[a<<1|1]+=lz[a];
    lz[a]=0;
}
inline void build(int a,int l,int r){
    if(l==r){
        tr[a]=b[l];return;
    }
    int mid=(l+r)>>1;
    build(a<<1,l,mid);build(a<<1|1,mid+1,r);
}
inline void add(int a,int l,int r,int l1,int r1,int x){
    if(r<l1||r1<l)return;
    if(l1<=l&&r<=r1){
        lz[a]+=x;
        if(l==r)tr[a]+=x;
        return;
    }
    push(a,l,r);
    int mid=(l+r)>>1;
    add(a<<1,l,mid,l1,r1,x);add(a<<1|1,mid+1,r,l1,r1,x);
}
inline ll ask(int a,int l,int r,int k){
    if(l==r)return tr[a];
    push(a,l,r);
    int mid=(l+r)>>1;
    if(k<=mid)return ask(a<<1,l,mid,k);
    else return ask(a<<1|1,mid+1,r,k);
}
inline ll qry(int l){
    if(tag[l]==m)return b[l];
    tag[l]=m;
    return b[l]=ask(1,1,n,l);
}
inline ll query(int l,int r,int p){
    ll ans=qry(l);
    if(ans%p==0)return 0;
    if(p==1)return 1;
    if(l==r)return (ans%p+(ans>p)*p)%p;
    int f=min(r,l+5);
    for(int i=l+1;i<=f;i++){
        if(qry(i)==1){
            f=i;break;
        }
    }
    ll t=qry(f),q=0;
    for(int i=f-1;i>=l+1;i--){
        q=t,t=1;
        ll tmp=qry(i);
        while(q--){
            t*=tmp;
            if(t>=phi[p])return qpow(ans%p,query(l+1,r,phi[p])+phi[p],p);
        }
    }
    return qpow(ans%p,t,p);
}
int main(){
    Euler(2e7);memset(tag,-1,sizeof(tag));
    n=read(),m=read();
    for(int i=1;i<=n;i++)b[i]=read();
    build(1,1,n);
    while(m--){
        int op=read();
        if(op==1){
            int l=read(),r=read(),x=read();
            add(1,1,n,l,r,x);
        }else{
            int l=read(),r=read(),p=read();
            printf("%lld\n",query(l,r,p));
        }
    }
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

 +本文作者：luyouqi233。 　　　　　　　　　　　　　　+

 +欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++