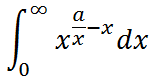洛谷4525 & 4526：【模板】自适应辛普森法——题解

参考：https://phqghume.github.io/2018/05/19/%E8%87%AA%E9%80%82%E5%BA%94%E8%BE%9B%E6%99%AE%E6%A3%AE%E6%B3%95/ 以及洛谷不多的题解。

辛普森推导过程就看参考吧，当然你要想看懂推导需要：

1.会高中导数那点东西，至少知道原函数怎么求。

2.粗略了解定积分。

3.知道微积分第一、第二基本定理（从知乎上找的：https://www.zhihu.com/question/21439225）。

然后推导就很简单了，实际上就是用的是将任意曲线近似转换成二次函数曲线去求。

————————————————————

https://www.luogu.org/problemnew/show/P4525

计算积分

结果保留至小数点后6位。

数据保证计算过程中分母不为0且积分能够收敛。

这就是自适应辛普森的板题了，eps开到1e-12大概就能过了。

（话说为什么要“自适应”？那当然是因为精度的原因啦，我们左右分一下将答案求和和一个区间的答案比较一下没有多少误差就return就行啦。）

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-12;
dl a,b,c,d,L,R;
inline dl f(dl x){
    return (c*x+d)/(a*x+b);
}
inline dl simpson(dl l,dl r){
    dl mid=(l+r)/2;
    return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
inline dl asr(dl l,dl r,dl ans){
    dl mid=(l+r)/2;
    dl l1=simpson(l,mid),r1=simpson(mid,r);
    if(fabs(l1+r1-ans)<eps)return l1+r1;
    return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
    scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&L,&R);
    printf("%lf\n",asr(L,R,simpson(L,R)));
    return 0;
}

————————————————————

https://www.luogu.org/problemnew/show/P4526

计算积分

保留至小数点后5位。若积分发散，请输出"orz"。

挺吓人的，但思考a<0显然就发散了。

a>=0时a越大收敛得越慢，于是打表，大概得出来x=12时就已经约为0了。

于是L=eps，R=12跑一遍自适应辛普森法即可。

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-12;
dl a;
inline dl f(dl x){
    return pow(x,a/x-x);
}
inline dl simpson(dl l,dl r){
    dl mid=(l+r)/2;
    return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
inline dl asr(dl l,dl r,dl ans){
    dl mid=(l+r)/2;
    dl l1=simpson(l,mid),r1=simpson(mid,r);
    if(fabs(l1+r1-ans)<eps)return l1+r1;
    return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
    scanf("%lf",&a);
    if(a<0)puts("orz");
    else printf("%.5lf\n",asr(eps,12,simpson(eps,12)));
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

 +本文作者：luyouqi233。 　　　　　　　　　　　　　　+

 +欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++