HDU5446：Unknown Treasure——题解

http://acm.hdu.edu.cn/showproblem.php?pid=5446

求C(n,m)%(p1p2…pk)的值，其中pi均为质数。

参考：https://www.cnblogs.com/linyujun/p/5199684.html

预备知识：

1.Lucas定理（图片来自百科）：当p为素数时，有

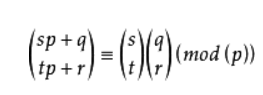
2.中国剩余定理：

3.求逆元。

根据中国剩余定理可知，我们求C(n,m)%(p1p2…pk)，实际就是在求解同余方程组：

C(n,m)%p1=a1

C(n,m)%p2=a2

……

C(n,m)%p3=a3

最终求得的C(n,m)即是在%(p1p2…pk)意义下的。

根据lucas定理，我们能立刻求出所有a的值。 

在那之后用中国剩余定理求解即可。

（另外如果逆元不存在的话我就不知道怎么做了emmm……不过看数据貌似避开了这个问题）

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
ll qpow(ll k,ll n,ll p){
    ll ans=1;
    while(n){
        if(n&1)ans=ans*k%p;
        k=k*k%p;n>>=1;
    }
    return ans;
}
ll mul(ll a,ll b,ll p){
    ll ans=0;
    while(b){
        if(b&1)ans=(ans+a)%p;
        a=(a<<1)%p;b>>=1;
    }
    return ans;
}
ll C(ll n,ll m,ll p){
    if(n<m)return 0;
    if(n==m)return 1;
    if(m>n-m)m=n-m;
    ll cn=1,cm=1;
    for(ll i=0;i<m;i++){
        cn=cn*(n-i)%p;
        cm=cm*(m-i)%p;
    }
    return cn*qpow(cm%p,p-2,p)%p;
}
ll lucas(ll n,ll m,ll p){
    ll ans=1;
    while(n&&m&&ans){
        ans=ans*C(n%p,m%p,p)%p;
        n/=p;m/=p;
    }
    return ans;
}
int t;
ll n,m,k,p[11],r[11],P;
int main(){
    cin>>t;
    while(t--){
        cin>>n>>m>>k;P=1;
        for(int i=1;i<=k;i++){
            cin>>p[i];P*=p[i];
            r[i]=lucas(n,m,p[i]);
        }
        ll ans=0;
        for(int i=1;i<=k;i++){
            ll w=P/p[i],inv=qpow(w%p[i],p[i]-2,p[i]);
            ans=(ans+mul(w*inv,r[i],P))%P;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

 +本文作者：luyouqi233。 　　　　　　　　　　　　　　+

 +欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++