BZOJ3076 & 洛谷3081：[USACO2013 MAR]Hill Walk 山走——题解

http://www.lydsy.com/JudgeOnline/problem.php?id=3076

https://www.luogu.org/problemnew/show/P3081#sub

有N(1 <= N <= 100,000)座小山，每座山所占的区域用直线(x1, y1) 到 (x2, y2)来表示（x1 < x2 并且 y1 < y2）。也就是说这些山用笛卡尔坐标系里的线段来表示，这些用于表示小山的线段都没有任何交点，第一座山的一端位于(x1, y1) = (0,0)

贝西从(0,0)开始在第一座山上漫步，一旦贝西到了一座山，她会一直走到该山的终点，这时，她会从边缘处起跳，如果她降落到另一座山上，她会继续在新的山上漫步。贝西起跳后沿y轴方向下落，如果贝西不能降落到一座山上，她会一直下落，直到到达y轴的负无穷大位置(y = -infinity)。

每座用线段表示的山 (x1, y1) -> (x2, y2)包含(x1, y1)这个点，但不包含(x2, y2) ，请计算出贝西总共在多少座山上漫步了。

……这道题网上几乎没找到题解……所以是参考了标程的（我也看不懂英文啊……）

首先说一下解题思路：我们显然要走一遍线段，并且在掉落的时候以O(logn)的速度查找到你应当掉落在那个线段上。那么复杂度就是O(nlogn)了。

显然的思路，我们记录当前走在了哪个线段，用set维护接下来**可能**走的线段，取出我们所要的线段即可。

（PS：“可能”指你所在的坐标的x在某个线段的x区间内）

走在了哪个线段没有难度，本代码的cur就是做这个的。

找接下来可能走的线段（并且及时剔除掉走过/不能走到的线段），扫描线即可解决。

那么这题的难点就在于我们如何排序（也就是set的比较方法）来取出我们所要的线段。

先画个图感性理解一下，黑点是我们所在的位置，编号就是我们排好序之后的编号。

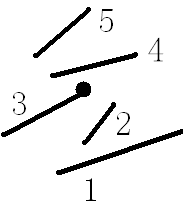
（我们所在的位置是3，显然只需要跳到3-1=2的编号的那条边，我们就实现了走的动作。）

 设比较的两条线段a,b，则分为两种情况：

1.ax2<bx2（eg：a=5,b=4或a=2,b=4）：

 我们把a的右端点和b的左端点连线，显然发现这条线段将这两条线划分开来，上面的线编号大，下面的线编号小。

 2.ax2>bx2（eg：a=1,b=3或a=4,b=3）：

 同1的思路，其实只是把a和b颠倒而已。

 我们可以通过斜率来比较两条线的位置。

（PPS：貌似可以两条线分别取一个不同方向的点连线貌似就可以，不必非得按照题解的连线方法）

（PPPS：可能有这种情况（举一个1的例子）：

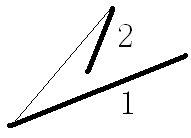
这时候我们只需要平移一下就好了。

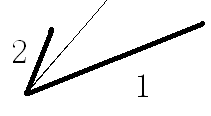
所以用斜率判断是最准确的。）

 

————————————————————

一些小细节，比如说你已经在最下层线段没法在往下走时及时跳出

#include<set>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+5;
inline int read(){
    int X=0,w=1;char ch=0;
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
    return X*w;
}
struct edge{
    int x1,x2,y1,y2,id;
    bool operator <(edge const& a)const{
        if(x2<a.x2){
            return (ll)(y2-a.y1)*(ll)(a.x2-a.x1)<(ll)(a.y2-a.y1)*(ll)(x2-a.x1);
        }else{
            return (ll)(a.y2-y1)*(ll)(x2-x1)>(ll)(y2-y1)*(ll)(a.x2-x1);
        }
    }
}e[N];
struct event{
    int x,y,id;
    bool operator <(event const& a)const{
        return x<a.x||(x==a.x&&y<a.y);
    }
}f[2*N];
set<edge>s;
set<edge>::iterator it1;
set<edge>::iterator it2;
int main(){
    int n=read();
    for(int i=1;i<=n;i++){
        e[i].x1=read();e[i].y1=read();
        e[i].x2=read();e[i].y2=read();
        e[i].id=i;
        f[i*2-1].x=e[i].x1;f[i*2].x=e[i].x2;
        f[i*2-1].y=e[i].y1;f[i*2].y=e[i].y2;
        f[i*2-1].id=f[i*2].id=i;
    }
    sort(f+1,f+2*n+1);
    s.insert(e[1]);
    int cur=1,tot=1;
    for(int i=2;i<=2*n;i++){
        event ev=f[i];
        edge ed=e[ev.id];
        if(ev.x==ed.x1)s.insert(ed);
        else if(ev.id==cur){
            it1=s.find(ed);
            if(it1==s.begin())break;
            it2=it1;--it2;
            cur=it2->id;
            s.erase(it1);
            tot++;
        }else s.erase(ed);
    }
    printf("%d\n",tot);
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++