POJ2826：An Easy Problem?!——题解（配特殊情况图）

http://poj.org/problem?id=2826

题目大意：给两条线，让它接竖直下的雨，问其能装多少横截面积的雨。

————————————————————————————

水题，看题目即可知道。

但是细节是真的多……不过好在两次AC应该没算被坑的很惨（全程没查题解）。

推荐交之前看一下讨论版的数据，方便一次AC（我第一次就是作死直接交了结果我自己都想好的情况忘了写了……）

相信看到这篇题解的人都看过题了，那么先说细节：

1.C++提交（G++不知道为什么WA了……）

2.精度

3.特殊情况，看看下面哪种情况你没有考虑到（以下都是没法装水的情况）：

 

 

 

 

 

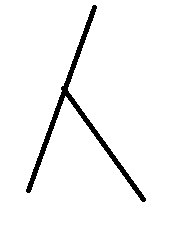
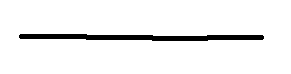
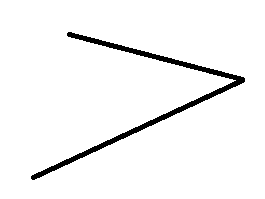
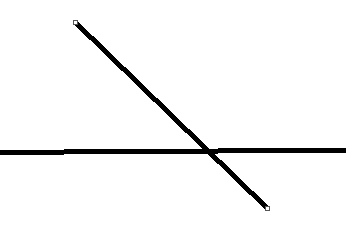
 还有一种能够接水的情况：

将上面考虑完了，应该就差不多了。

那么说一下正解：

1.ko掉所有平行情况。（图3）

2.ko掉所有不相交情况。（图6）

3.ko掉所有斜率为0的情况。（图5）

4.上述两种情况完成后，求交点。

5.发现图1和图7情况只存在于斜率同号的情况下，特判之。

6.图2和图4一并解决：从交点处画一条平行于x的线，如果在该线上方的点的个数不为2，则不能接水。

7.上述情况讨论完后一定能接水，从6中获得的两个点取y值最小的点画一条平行于x的线，则围成的面积即为所求

总结：

线关系和线交点的题，细节较多，代码实现较长较繁琐，不推荐读下面代码。

#include<cstdio>
#include<queue>
#include<cctype>
#include<cstring>
#include<stack>
#include<cmath>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-6;
const dl INF=2147483647;
struct point{
    dl x;
    dl y;
}p[5];
inline point getmag(point a,point b){
    point s;
    s.x=b.x-a.x;s.y=b.y-a.y;
    return s;
}
inline dl multiX(point a,point b){
    return a.x*b.y-b.x*a.y;
}
inline dl multiP(point a,point b){
    return a.x*b.x+b.y*a.y;
}
inline bool parallel_mag(point a,point b){
    if(fabs(a.x*b.y-a.y*b.x)<eps)return 1;
    return 0;
}
inline bool check(point a,point b,point c,point d){
    if(multiX(getmag(c,d),getmag(c,a))*multiX(getmag(c,d),getmag(c,b))>eps)return 0;
    if(multiX(getmag(a,b),getmag(a,c))*multiX(getmag(a,b),getmag(a,d))>eps)return 0;
    return 1;
}
inline point intersection(point a,point b,point c,point d){
    point s;  
    dl a1=a.y-b.y,b1=b.x-a.x,c1=a.x*b.y-b.x*a.y;  
    dl a2=c.y-d.y,b2=d.x-c.x,c2=c.x*d.y-d.x*c.y;  
    s.x=(c1*b2-c2*b1)/(a2*b1-a1*b2);  
    s.y=(a2*c1-a1*c2)/(a1*b2-a2*b1);
    return s;
}
inline dl slope(point a,point b){
    if(fabs(a.x-b.x)<eps)return INF;
    return (a.y-b.y)/(a.x-b.x);
}
inline bool deng(point a,point b){
    if(fabs(a.x-b.x)<eps&&fabs(a.y-b.y)<eps)return 1;
    return 0;
}
inline bool pan(point s){
    dl k1=slope(p[1],p[2]);
    dl k2=slope(p[3],p[4]);
    if(fabs(k1)<eps||fabs(k2)<eps)return 0;
    if(k1>eps&&k2>eps){
        if(k2-k1>eps){
            if(-eps<p[4].x-p[2].x)return 0;
        }else{
            if(-eps<p[2].x-p[4].x)return 0;
        }
    }
    if(k1<-eps&&k2<-eps){
        if(k1<k2){
            if(p[3].x-p[1].x>-eps)return 0;
        }else{
            if(p[1].x-p[3].x>-eps)return 0;
        }
        return 1;
    }
    int ok=0;
    for(int i=1;i<=4;i++){
        if(p[i].y-s.y>eps){
            ok++;
        }
    }
    if(ok!=2)return 0;
    return 1;
}
dl area(){
    if(parallel_mag(getmag(p[1],p[2]),getmag(p[3],p[4])))return 0;
    if(!check(p[1],p[2],p[3],p[4]))return 0;
    point s=intersection(p[1],p[2],p[3],p[4]);
    if(!pan(s))return 0;
    int s1=0,s2=0;
    for(int i=1;i<=4;i++){
        if(p[i].y-s.y>eps){
            if(!s1)s1=i;
            else s2=i;
        }
    }
    point ns,nss,n1,n2;
    if(eps<p[s2].y-p[s1].y){
        ns.x=p[s1].x;ns.y=p[s1].y;
    }else{
        ns.x=p[s2].x;ns.y=p[s2].y;
    }
    nss.x=INF;nss.y=ns.y;
    n1=intersection(p[1],p[2],ns,nss);
    n2=intersection(p[3],p[4],ns,nss);
    return fabs(multiX(getmag(s,n1),getmag(s,n2)))/2;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        for(int i=1;i<=4;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
        if(p[1].x>p[2].x)swap(p[1],p[2]);
        if(p[3].x>p[4].x)swap(p[3],p[4]);
        printf("%.2f\n",area());
    }
    return 0;
}