Codeforces Round #258 (Div. 2)（A，B，C，D）

题目链接

A. Game With Sticks

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

After winning gold and silver in IOI 2014, Akshat and Malvika want to have some fun. Now they are playing a game on a grid made of nhorizontal and m vertical sticks.

An intersection point is any point on the grid which is formed by the intersection of one horizontal stick and one vertical stick.

In the grid shown below, n = 3 and m = 3. There are n + m = 6 sticks in total (horizontal sticks are shown in red and vertical sticks are shown in green). There are n·m = 9 intersection points, numbered from 1 to 9.

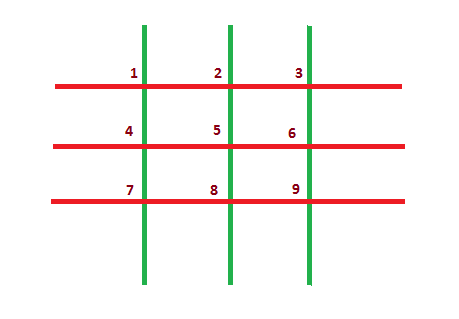
The rules of the game are very simple. The players move in turns. Akshat won gold, so he makes the first move. During his/her move, a player must choose any remaining intersection point and remove from the grid all sticks which pass through this point. A player will lose the game if he/she cannot make a move (i.e. there are no intersection points remaining on the grid at his/her move).

Assume that both players play optimally. Who will win the game?

Input

The first line of input contains two space-separated integers, n and m (1 ≤ n, m ≤ 100).

Output

Print a single line containing "Akshat" or "Malvika" (without the quotes), depending on the winner of the game.

Sample test(s)

input

2 2

output

Malvika

input

2 3

output

Malvika

input

3 3

output

Akshat

Note

Explanation of the first sample:

The grid has four intersection points, numbered from 1 to 4.

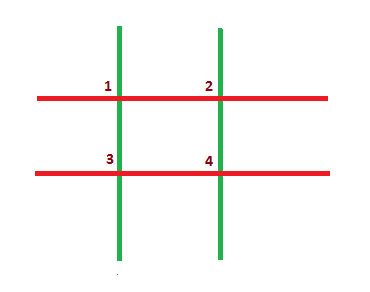
If Akshat chooses intersection point 1, then he will remove two sticks (1 - 2 and 1 - 3). The resulting grid will look like this.

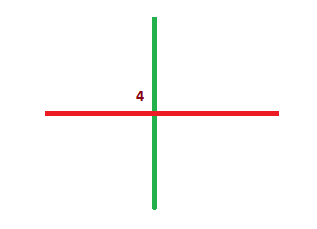
Now there is only one remaining intersection point (i.e. 4). Malvika must choose it and remove both remaining sticks. After her move the grid will be empty.

In the empty grid, Akshat cannot make any move, hence he will lose.

Since all 4 intersection points of the grid are equivalent, Akshat will lose no matter which one he picks.

题意 ：给定n×m根线，如图摆放，将交点从1到n×m编号，两个人轮流走到交点上，然后将经过这个交点的某条线移走，最后没有交点可走的人输。

思路 ：因为拿走一根线的话，所有别的跟这个线的交点也就没有了，所以实际上求的是min(n,m)对2取余。

//258A
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std ;

int main()
{
    int n, m ;
    while(scanf("%d %d",&n,&m) != EOF)
    {
        int s = min(n,m) ;
         if(s % 2)
            puts("Akshat") ;
         else puts("Malvika") ;
    }
    return 0 ;
}

 

B. Sort the Array

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

Being a programmer, you like arrays a lot. For your birthday, your friends have given you an array a consisting of n distinct integers.

Unfortunately, the size of a is too small. You want a bigger array! Your friends agree to give you a bigger array, but only if you are able to answer the following question correctly: is it possible to sort the array a (in increasing order) by reversing exactly one segment of a? See definitions of segment and reversing in the notes.

Input

The first line of the input contains an integer n (1 ≤ n ≤ 10⁵) — the size of array a.

The second line contains n distinct space-separated integers: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 10⁹).

Output

Print "yes" or "no" (without quotes), depending on the answer.

If your answer is "yes", then also print two space-separated integers denoting start and end (start must not be greater than end) indices of the segment to be reversed. If there are multiple ways of selecting these indices, print any of them.

Sample test(s)

input

3
3 2 1

output

yes
1 3

input

4
2 1 3 4

output

yes
1 2

input

4
3 1 2 4

output

no

input

2
1 2

output

yes
1 1

Note

Sample 1. You can reverse the entire array to get [1, 2, 3], which is sorted.

Sample 3. No segment can be reversed such that the array will be sorted.

Definitions

A segment [l, r] of array a is the sequence a[l], a[l + 1], ..., a[r].

If you have an array a of size n and you reverse its segment [l, r], the array will become:

a[1], a[2], ..., a[l - 2], a[l - 1], a[r], a[r - 1], ..., a[l + 1], a[l], a[r + 1], a[r + 2], ..., a[n - 1], a[n].

 

题意 ： 通过将数组a里的某一段逆置之后，能否将这个数组变成有序的。

思路 ：既然是逆置的，例如1 2 3 6 5 4 7 8 9

那就从头开始找大于下一个数的那个数的位置，然后再接着找小于下一个数的那个数的位置，将这两者之间的逆置，如果这样是有序的了，就yes，除此之外就是不可能的情况了，比如有两段需要逆置，或者这段逆置的也不是倒着有序的等等。

//258B
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>

using namespace std ;

int a[100010],b[100010] ;

int main()
{
    int n ;
    while(cin >> n)
    {
        for(int i = 0 ; i < n ; i++)
        {
            cin >> a[i] ;
            b[i] = a[i] ;
        }
        int be = -1,en = -1 ;
        for(int i = 0 ; i < n-1 ; i++)
        {
            if(a[i] > a[i+1])
            {
                be = i ;
                break ;
            }
        }
        if(be == -1) {puts("yes") ; puts("1 1");continue ;}
        int i ;
        for(i = be ; i < n-1 ; i++)
        {
            if(a[i] < a[i+1])
            {
                en = i ;
                break ;
            }
        }
        if(i == n-1) en = n-1 ;
        reverse(a+be,a+en+1) ;
        sort(b,b+n) ;
        for(i = 0 ; i < n ; i++)
        {
            if(a[i] != b[i]) break ;
        }
        if(i == n) {
                puts("yes") ;
        cout << be +1 << " "<< 1 + en <<endl ;
        }
        else puts("no") ;
    }
    return 0 ;
}

 

C. Predict Outcome of the Game

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

There are n games in a football tournament. Three teams are participating in it. Currently k games had already been played.

You are an avid football fan, but recently you missed the whole k games. Fortunately, you remember a guess of your friend for these kgames. Your friend did not tell exact number of wins of each team, instead he thought that absolute difference between number of wins of first and second team will be d₁ and that of between second and third team will be d₂.

You don't want any of team win the tournament, that is each team should have the same number of wins after n games. That's why you want to know: does there exist a valid tournament satisfying the friend's guess such that no team will win this tournament?

Note that outcome of a match can not be a draw, it has to be either win or loss.

Input

The first line of the input contains a single integer corresponding to number of test cases t (1 ≤ t ≤ 10⁵).

Each of the next t lines will contain four space-separated integers n, k, d₁, d₂ (1 ≤ n ≤ 10¹²; 0 ≤ k ≤ n; 0 ≤ d₁, d₂ ≤ k) — data for the current test case.

Output

For each test case, output a single line containing either "yes" if it is possible to have no winner of tournament, or "no" otherwise (without quotes).

Sample test(s)

input

5
3 0 0 0
3 3 0 0
6 4 1 0
6 3 3 0
3 3 3 2

output

yes
yes
yes
no
no

Note

Sample 1. There has not been any match up to now (k = 0, d₁ = 0, d₂ = 0). If there will be three matches (1-2, 2-3, 3-1) and each team wins once, then at the end each team will have 1 win.

Sample 2. You missed all the games (k = 3). As d₁ = 0 and d₂ = 0, and there is a way to play three games with no winner of tournament (described in the previous sample), the answer is "yes".

Sample 3. You missed 4 matches, and d₁ = 1, d₂ = 0. These four matches can be: 1-2 (win 2), 1-3 (win 3), 1-2 (win 1), 1-3 (win 1). Currently the first team has 2 wins, the second team has 1 win, the third team has 1 win. Two remaining matches can be: 1-2 (win 2), 1-3 (win 3). In the end all the teams have equal number of wins (2 wins).

 

题意 ：三个队伍，一共n场比赛，已经进行了k场，在已经进行的k场中，三个队伍分别赢了A，B，C场，|A-B|=d1.|B-C|=d2 .在符合这些条件的情况下，安排这k场比赛以及还未比的n-k场，要求最后三个队伍打平。

思路 ： 因为三个队伍要打平，所以n一定是可以整除3的，否则绝对无法打平。然后根据d1和d2的正负问题，即ABC的大小问题，分为正正、正负、负正、负负四种情况。

通过A+B+C=k与|A-B|=d1，|B-C|=d2，三式联合可求得ABC的表达式，然后再判断是不是满足各种要求

#include <cstdio>
#include <iostream>
#define LL long long

using namespace std ;

bool dose(LL n, LL k, LL d1,LL d2)
{
    for(int i = -1 ; i <= 1 ; i ++)
        for(int j = -1 ; j <= 1 ; j++)
        {
            if(i == 0 || j == 0)
                continue ;
            LL D1 = d1*i ,D2 = d2*j ;
            LL B = (k - D1 + D2) / 3 ;
            if((k - D1 + D2) % 3)  return false ;
            if(B >= 0 && B <= k)
            {
                LL A = D1+B,C = B-D2 ;
                if(A >= 0 && A <= k && C >= 0 && C <= k)
                    if(A <= n/3 && B <= n/3 && C <= n/3)
                        return true ;
            }
        }
    return false ;
}
int main()
{
    LL T,n,k,d1,d2 ;
    cin >> T;
    while(T--)
    {
        cin>>n >> k >> d1 >> d2 ;
        if(n % 3)
        {
            puts("no" );
            continue ;
        }
        bool flag = dose(n,k,d1,d2) ;
        if(flag) puts("yes") ;
        else puts("no") ;
    }
    return 0 ;
}

//A + B + C = k ---(1)
//|A - B| = d1  ---(a)
//|B - C| = d2  ---(b)
#include<cstdio>
#include<iostream>

using namespace std;

#define LL long long
LL n,k,d1,d2,ave,x;

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>k>>d1>>d2;
        if(n % 3)//如果n无法整除3，则无法达到三个平局
        {
            puts("no") ;
            continue ;
        }
        ave = n/3;
        bool flag = false ;
        //A>B&&B>C时，A-B=d1,B-C=d2
        //最小的是C，最大的是A
        //通过式子连立可求出C= (k-d1-2*d2)/3
        if( (k-d1-2*d2) % 3 == 0 && (k-d1-2*d2) >= 0)//C必须是整数并且大于等于0
        {
            x = (k-d1-2*d2)/3;
            if(x+d1+d2<=ave)//三者之中最大的是A，只要A小于等于平均值，BC都会满足
                flag = true;
        }
        //A>B&&B<C时，A-B=d1,B-C=-d2
        //最小的是B，AC无法辨大小
        //通过式子连立可求出B = （k-d1-d2）/3
        if( (k-d1-d2) % 3 == 0 && (k-d1-d2) >= 0)
        {
            x = (k-d1-d2)/3;
            if(x+d1<=ave&&x+d2<=ave)//AC比B大，只要判断AC是不是都小于平均数即可
                flag = true;
        }
        //A<B&&B<C时，A-B=-d1,B-C=-d2
        //最小的是A，C最大
        //通过式子连立可求出A = （k-2*d1-d2）/3
        if( (k-2*d1-d2) % 3 == 0 && (k-2*d1-d2) >= 0)
        {
            x = (k-2*d1-d2)/3;
            if(x+d1+d2 <= ave)
                flag = true;
        }
        //A<B&&B>C时，A-B=-d1,B-C=d2
        //最大的是B，AC无法辨大小
        //通过式子连立可求出A = （k-2*d1+d2）/3,C=(k+d1-2*d2)
        if( (k+d2-2*d1)%3==0 && (k+d2-2*d1)>=0 && (k+d1-2*d2)%3==0 && (k+d1-2*d2)>=0)
        {
            x = (k+d2-2*d1)/3;
            if(x+d1 <= ave)
                flag = true;
        }
        if(flag) puts("yes");
        else puts("no");
    }
    return 0;
}

 

 

D. Count Good Substrings

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

We call a string good, if after merging all the consecutive equal characters, the resulting string is palindrome. For example, "aabba" is good, because after the merging step it will become "aba".

Given a string, you have to find two values:

1. the number of good substrings of even length;
2. the number of good substrings of odd length.

Input

The first line of the input contains a single string of length n (1 ≤ n ≤ 10⁵). Each character of the string will be either 'a' or 'b'.

Output

Print two space-separated integers: the number of good substrings of even length and the number of good substrings of odd length.

Sample test(s)

input

bb

output

1 2

input

baab

output

2 4

input

babb

output

2 5

input

babaa

output

2 7

Note

In example 1, there are three good substrings ("b", "b", and "bb"). One of them has even length and two of them have odd length.

In example 2, there are six good substrings (i.e. "b", "a", "a", "b", "aa", "baab"). Two of them have even length and four of them have odd length.

In example 3, there are seven good substrings (i.e. "b", "a", "b", "b", "bb", "bab", "babb"). Two of them have even length and five of them have odd length.

Definitions

A substring s[l, r] (1 ≤ l ≤ r ≤ n) of string s = s₁s₂... s_n is string s_ls_l + 1... s_r.

A string s = s₁s₂... s_n is a palindrome if it is equal to string s_ns_n - 1... s₁.

 

题意 ： 如果将一个字符串中连续相同的字符合并成一个该字符之后，合并之后的字符串如果是回文的话，我们定义原串为good。然后给你一个字符串，让你找他的是good的子串中长度为奇数的串的个数以及长度为偶数的串的个数。

思路 ：先看偶数长度的串，子串 s_ls_l + 1... s_r如果是偶数长度的话，那么左边界 L 和右边界r，肯定一个在奇数位置一个在偶数位置，这样长度就是偶数。对，忘了说，因为可以合并连续的相同的字母，所以只要一个串首跟尾是同字母，就肯定是good。求偶数长度的话，只要求出奇数位置的a，偶数位置的a有多少个，两者相乘，就可以求出以a为头和尾的字符串的并且长度是偶数的串的个数。同理，奇数长度的串，只要两者都在奇数位置或者都在偶数位置就可以。

//258D
#include <stdio.h>
#include <string.h>
#include <iostream>

typedef long long LL ;

using namespace std ;

string str ;

LL calcu(LL x)
{
    return x * ( x - 1 ) / 2 ;
}
int main()
{
    while(cin >> str)
    {
        LL odda = 0,oddb = 0, evena = 0 ,evenb = 0 ;
        for(int i = 0 ; i < str.length() ; i++)
        {
            if(str[i] == 'a')
            {
                if(i & 1)
                    odda ++ ;
                else evena ++ ;
            }
            else
            {
                if(i & 1)
                    oddb ++ ;
                else evenb ++ ;
            }
        }
        LL Odd = evena*odda+evenb*oddb ;
        LL Even = str.length() + calcu(evena) + calcu(oddb) + calcu(odda) + calcu(evenb) ;
        cout<< Odd <<" "<< Even << endl ;
    }
    return 0 ;
}