IMO 2024 (P1, P5)

水群的时候看到题了。挑点看上去能做的做做。
不保证做法对。

Problem 1.
求所有实数 \(\alpha\) 满足：对任意正整数 \(n\)，整数 \(\lfloor \alpha \rfloor + \lfloor 2\alpha \rfloor + \cdots + \lfloor n\alpha \rfloor\) 均为 \(n\) 的倍数.

sol: 别急。

Problem 5.
有一个游戏，提供了一个 2024 行 2023 列的网格，上面恰有 2022 个坏人，且除了第 1 行和第 2024 行，每一行都恰有一个坏人；每一列都至多有一个坏人。你每次可以做一个尝试：从第 1 行的任意位置出发，向有公共边的相邻格走一步（可以走到之前走过的位置），如果遇到坏人就结束尝试。每次尝试后你都有记忆，可以记住坏人的位置。当你走到第 2024 行的任意位置时，游戏结束。
求最小的正整数 \(n\)，使得无论坏人位置的分布如何，都能确保你在最优策略下至多进行 \(n\) 次尝试就能结束游戏。

sol：怎么大家都觉得这题挺简单的，是不是也没那么简单。

一开始想了一个 \(\log\) 级别的答案的构造，后来群友说答案是 3，给我直接干碎了。解法是这样：
考虑先找到第 \(2\) 行的坏人位置，这个好找。从 \((1,1)\) 出发，先走到 \((2,1)\) （如果这里本身是坏人那就找到了），然后向右扫。假设坏人坐标是 \((2, x)\).

• $ 1 < x < 2023$ : 我们有一种想法：找到一种方式绕到 \((2, x)\) 的下面直接走到最后一行。用同样的方法找到第 3 行的坏人 \((3, y)\). 不难发现无论 \(y\) 与 \(x\) 的关系如何，我们都有办法构造一条路径 \((1, k) \leadsto (2, k) \leadsto (3, k) \leadsto (3, x) \leadsto \cdots \leadsto (2024, x)\) ，原因就是因为 \((3, y)\) 只挡住了 \((2, x)\) 的一边，只要找到一个数 \(k\) 满足 \(k \neq x, k \neq y\) 且 \(k\) 在 \(y\) 相对于 \(x\) 的异侧即可。因为 \(1 < x < 2023\)，我们肯定能找到这样的 \(k\)。这里使用了 3 步。
  

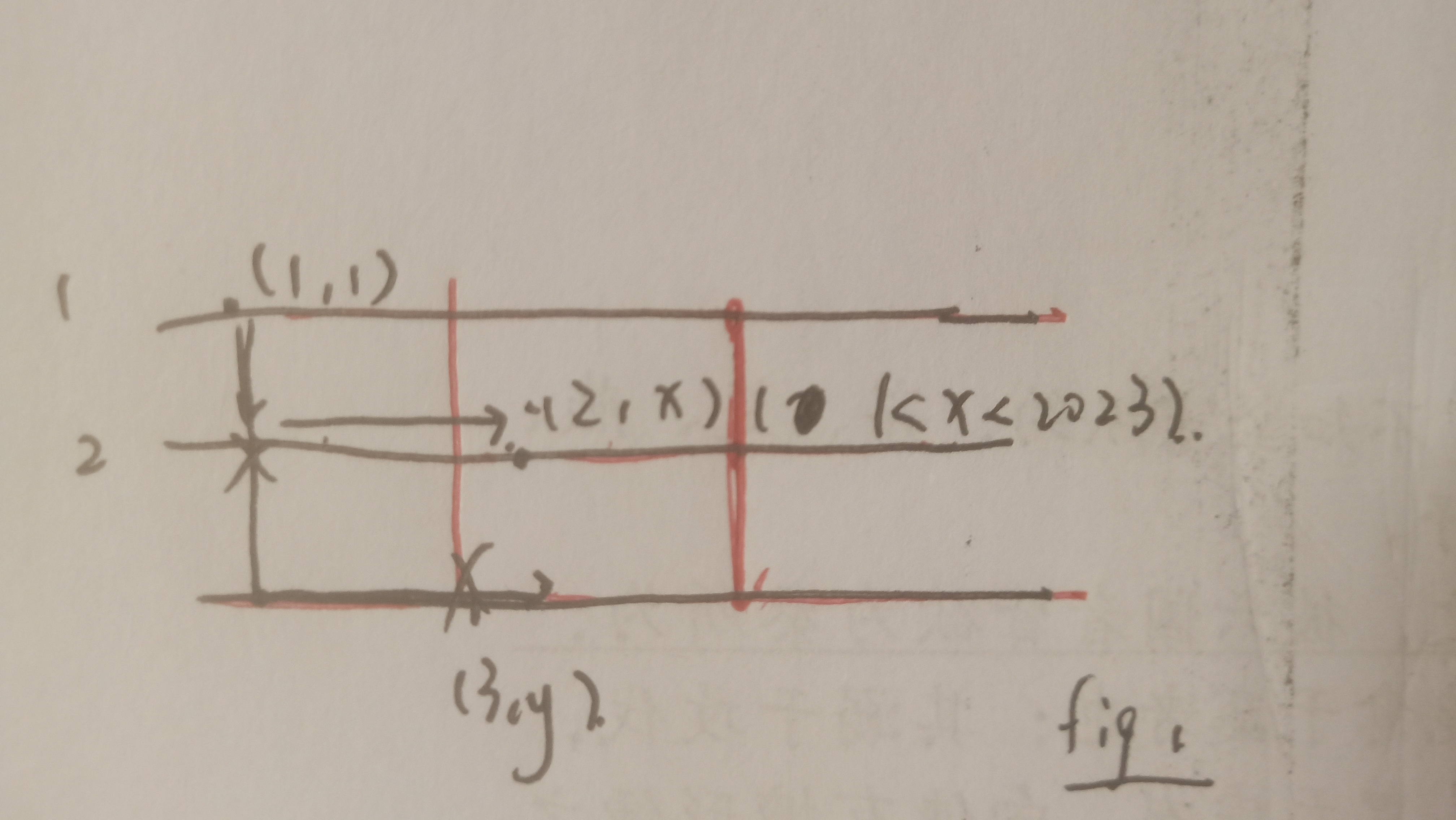
• \(x = 1\) 或 \(x = 2023\) : 不难发现这两种情况是对称的，接下来只讨论 \(x = 1\)。我们可能还会考虑继续找第 3 行的坏人位置，但是如果是 \((3, 2)\) 的话，局面似乎没有化简。这一次没有任何用。然后第 4 行找到 \((4, 3)\) 啥的靠在一起，这个就毁了。然后我就在这边做了些二分什么的，得到 \(\log\) 做法。
  这个显然不够牛啊，我们要向一个比较优秀的尝试的方法，使得这一次尝试能找到一个比较厉害的路径和得到尽可能多的合法点（行，列）而且要联通。
  考虑如下构造：我们做一次尝试：\((1, 1) \leadsto (1, 2) \leadsto (2, 2) \leadsto (2, 3) \leadsto (3, 3) \leadsto (3, 4) \leadsto \cdots\)，每次一右一下走格线。如果没碰到坏人那么就游戏结束；否则，假设我们碰到的坏人位置在 \(X\)。如果最后一次移动是向右（即图中 \(X_1\)）那么我们第三次尝试可以沿着上一次的路径走到 \(X_1\) 前一步然后向左走到底，然后向下走到底。如果最后一次是向下（即图中 \(X_2\)）那么我们第三次尝试可以沿路径走到 \(X_2\) 前两步直接向下走一步，然后向左走到底，向下走到底。这里可以看图。（其实可以换一种想法，就是我目前的尝试所发现的能走的点能否把第 1 行和第 2024 行联通，图中红色所标的就是能走的点构成的连通块）这样我们也只需要 3 次。
  

似乎没有更牛的构造了。\(n \le 2\) 不行怎么证。