CF1473E Minimum Path | Day7 path

说在前面

模拟赛撞题了，而我这场没打，/fad

题意简述

给一个\(n\)个点\(m\)条边的无向图，定义路径\(E\)的代价为

\[\sum_{i \in E} w_i + \min \{w_i\} + \max \{w_i\} \]

求从\(1\)出发，以\(2 \sim n\)为终点的最小代价。

测试点编号	\(n,m\)
\(1 \sim 2\)	\(\le 10\)
\(3 \sim 4\)	\(\le 100\)
\(5 \sim 6\)	\(\le 1000\)
\(7 \sim 8\)	\(\le 10 ^ 4\)
\(9 \sim 10\)	\(\le 2 \times 10 ^ 5\)
（以上数据范围根据模拟赛）

简单口胡

我们看一下式子，就会发现这玩意等于

\[\sum_{i \in E,w_i \not = \max\{w_i\},w_i \not= \min\{w_i\}} w_i + 2\max\{w_i\} \]

也就是减掉了\(\min\{w_i\}\)并且\(\max\{w_i\}\)是两倍贡献。

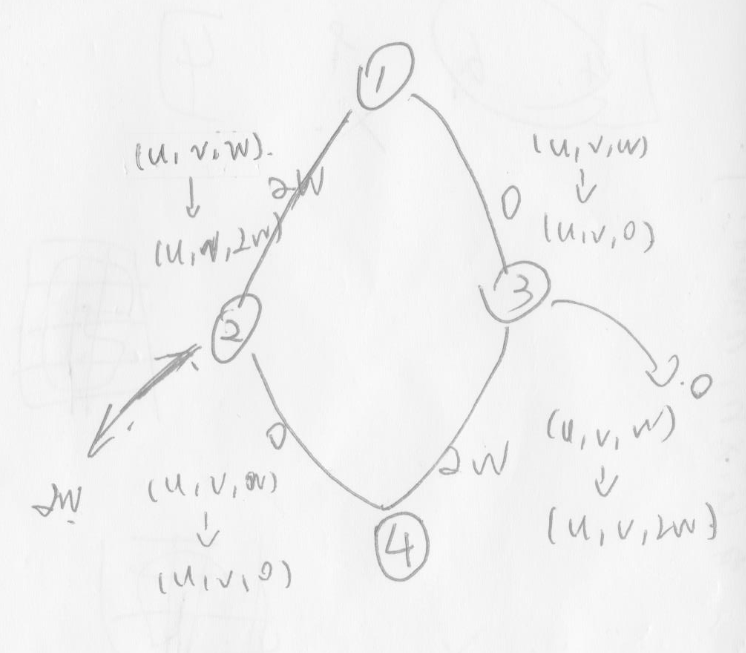
考虑分层图最短路，第一层为原图，第二层为\(0\)图，第三层为\(2w\)图，第四层两个都有

然后根据上图进行连边跑一遍dijkstra既珂。

# include <bits/stdc++.h>

using namespace std;

template <typename T> void read(T &x)
{
    int w = 1;
    x = 0;
    char ch = getchar();
    while(!isdigit(ch))
    {
        if(ch == '-') w = -1;
        ch = getchar();
    }
    while(isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    x *= w;
    return;
}

template <typename T> void write(T x)
{
    if(x < 0) putchar('-'),x = -x;
    if(x >= 10) write(x / 10);
    char ch = (x % 10) + 48;
    putchar(ch);
    return;
}

const int N = 2e5,M = 2e5;
int n,m;
struct edge
{
    int v;
    long long w;
    edge(int _v,long long _w) : v(_v),w(_w) {}
};

vector <edge> g[N << 2];

void add(int u,int v,long long w)
{
    g[u].push_back(edge(v,w));
    // g[v].push_back(edge(u,w));
    return;
}

long long dis[N << 2];

struct node
{
    int x;
    long long val;
    node() {}
    node(int _x,long long v) : x(_x),val(v) {}
};
priority_queue <node> q;
bool vis[N << 2];
bool operator < (const struct node x,const struct node y)
{
    return x.val > y.val;
}

void dij(void)
{
    for(int i = 1; i <= n * 4; i++) dis[i] = 1e12;
    dis[1] = 0;
    // vis[1] = 1;
    q.push(node(1,0));
    while(!q.empty())
    {
        int x = q.top().x;
        q.pop();
        if(vis[x]) continue;
        vis[x] = 1;
        for(int i = 0; i < (int)g[x].size(); i++)
        {
            int v = g[x][i].v;
            if(dis[v] > dis[x] + g[x][i].w)
            {
                dis[v] = dis[x] + g[x][i].w;
                q.push(node(v,dis[v]));
            }
        }
    }
    return;
}

int main(void)
{
    read(n),read(m);
    for(int i = 1; i <= m; i++)
    {
        int u,v;
        long long w;
        read(u),read(v),read(w);
        add(u,v,w);
        add(v,u,w);
        for(int j = 1; j < 4; j++)
        {
            add(u + j * n,v + j * n,w);
            add(v + j * n,u + j * n,w);
        }
        add(u,v + n,0);
        add(v,u + n,0);
        add(u,v + 2 * n,2 * w);
        add(v,u + 2 * n,2 * w);
        add(u + n,v + 3 * n,2 * w);
        add(v + n,u + 3 * n,2 * w);
        add(u + 2 * n,v + 3 * n,0);
        add(v + 2 * n,u + 3 * n,0);
    }
    dij();
    for(int i = 2; i <= n; i++)
    {
        write(min(dis[i],dis[i + 3 * n]));
        putchar(' ');
    }
    return 0;
}