平面最近点对

给定\(n\)个点\((x_1,y_1),(x_2,y_2,\cdots,(x_n,y_n)\)，求最近点对，即

\[\min_{i \not= j}\{\text{dis}(i,j)\} \]

其中\(\text{dis}(i,j)\)为点\(i\)和点\(j\)的距离，\(n \le 200000\)。

有一个很简单的\(\mathcal{O}(n ^ 2)\)做法，就是枚举\(i,j\)然后算距离，这里不展开讲。

讲一下分治的做法：
每次用一条直线（我称为分界线）将整个平面分成两部分\(L,R\)，将点分成两部分，如图。

算出两边的最近点对距离\(dis_L,dis_R\)，考虑如何算出\(L \to R\)的最近点对。

有一种比较简单的方法是在\(L\)当中枚举点和每一个\(R\)配对，复杂度太高了。

考虑什么样的情况对答案的更新是有效的。

设\(\delta = \min(dis_L,dis_R)\)，在这条分界线左右\(\delta\)远处作两条平行的直线，如图。

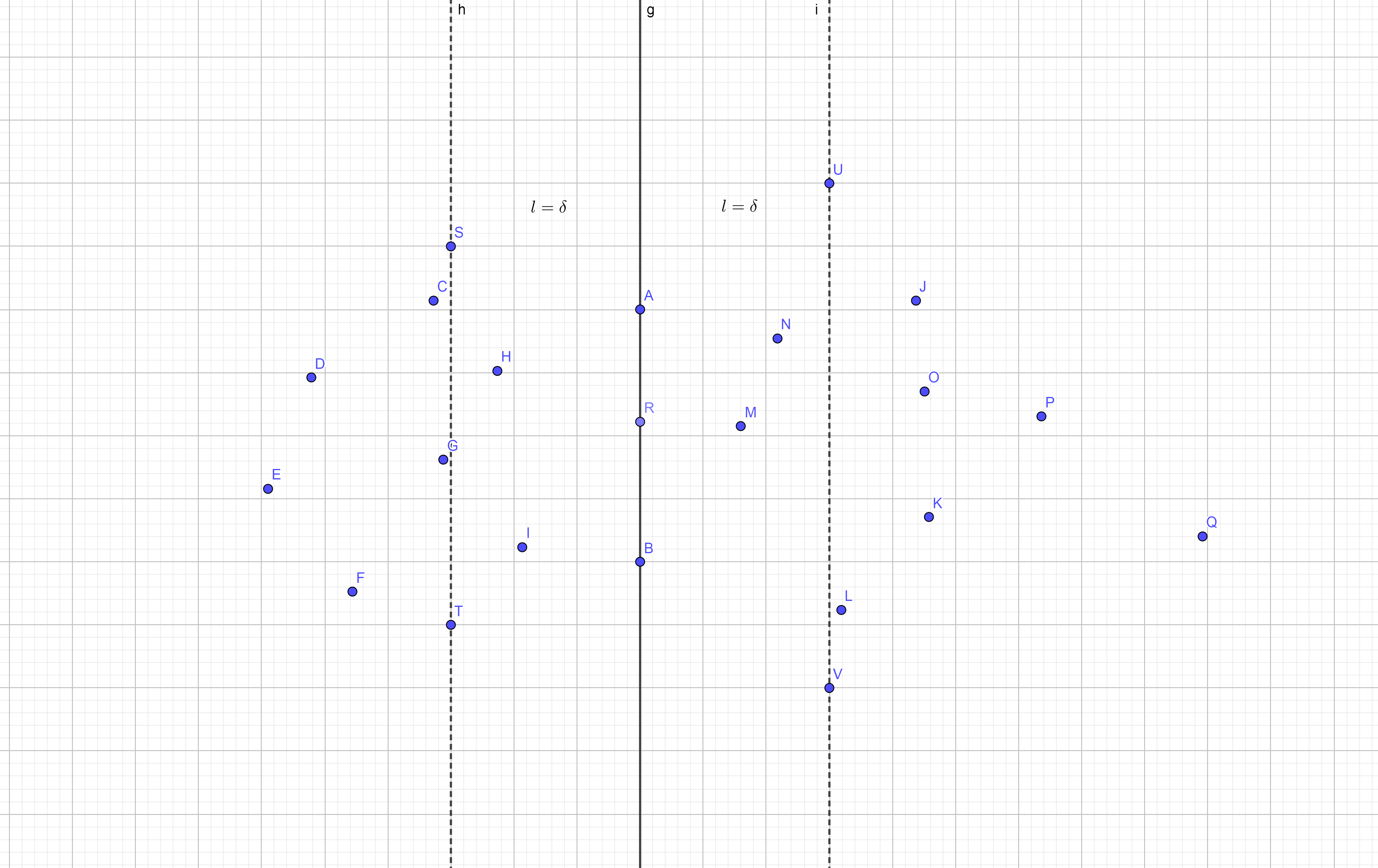
例如我现在考虑点R，以其为圆心，\(\delta\)为半径作圆，其中与右边那条虚线所框出来的点就是有意义的点，如图。

（N,M）
因为圆不好整，所以补成矩形。

证明：这个矩形里最多只有\(6\)个点。
将其分成六个等大的小矩形，长\(\frac{2}{3}\delta\)，宽\(\frac{1}{2}\delta\)，反证，如果个数\(>6\)，那么有一个矩形就会有\(2\)个点，这两个点的最远距离为\(\sqrt{\left(\frac{2}{3}\delta\right)^2 + \left(\frac{1}{2}\delta\right)^2} = \frac{5}{6}\delta < \delta\)，不符合\(\delta\)定义。

于是\(O(n\log{n})\)分治解决。