高 j 轨道上价核子波函数密度分布
高 \(j\) 轨道即高 \(l\) 轨道，\(j\) 是 \(l\) 与 \(s\) 的耦合：
可以先不考虑自旋，定性了解氢原子波函数的几率分布。
1. 氢原子波函数
氢原子波函数为
其密度为
所以密度分布是轴对称的。
用Sympy中的函数，可以绘制密度图。
首先绘制 \(|r*R_{nl}(r)|^2 \sim r\) 的图，取 \(l=4\)，这里 \(n\) 是主量子数：\(n = n_r + l + 1, ~~n, l = 0, 1, \cdots\)。
from sympy.physics.hydrogen import *
from sympy.abc import n, Z
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
#help(R_nl)
l = 4
def f(r):
return (r*R_nl(5,4,r))**2
I = quad( f, 0, 100 ); print("I = ", I) # 检验归一化
x = np.arange(0, 100, 0.1)
y1 = [(r*R_nl(l+1, l, r))**2 for r in x ]
y2 = [(r*R_nl(l+2, l, r))**2 for r in x ]
y3 = [(r*R_nl(l+3, l, r))**2 for r in x ]
plt.plot(x, y1, label=r"$r^2|R_{54}(r)|^2$");
plt.plot(x, y2, label=r"$r^2|R_{64}(r)|^2$");
plt.plot(x, y3, label=r"$r^2|R_{74}(r)|^2$");
plt.xlabel(r"$r ~~ (\AA)$")
plt.ylabel(r"$r^2|R_{nl}|^2$", fontsize=12);
plt.legend()
plt.show()
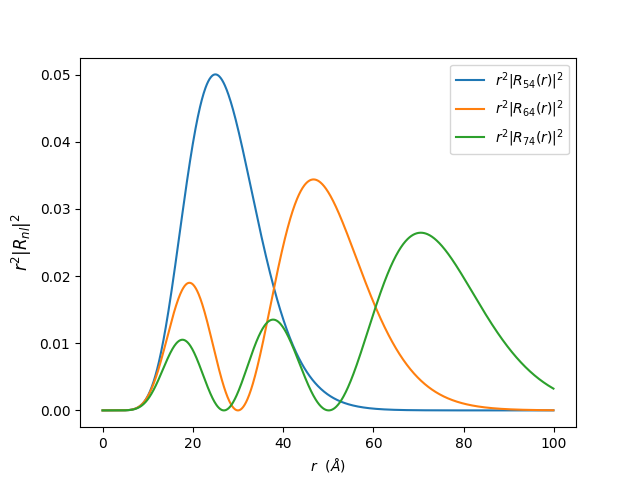
上图是几率密度与 \(r\) 的关系，有 \(n_r\) 个节点。可以非常简单地想象，有 \(n_r\) 层几率球壳。
然后绘制 \(|Y_{lm}|^2 \sim \theta, \phi\) 的图
import numpy as np
import matplotlib.pyplot as plt
from scipy import special
import mpl_toolkits.mplot3d.axes3d as axes3d
theta, phi = np.linspace(0, np.pi, 100), np.linspace(0, 2*np.pi, 100)
THETA, PHI = np.meshgrid(theta, phi)
help(special.lpmv)
m = 4
l = 4
#R = 0
#for m in np.arange(-l, l+1):
# R += abs(special.sph_harm(m,l,THETA,PHI))**2
R = abs(special.sph_harm(m,l,PHI,THETA))**2
X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)
fig = plt.figure()
ax = fig.add_subplot(1,1,1, projection='3d')
plot = ax.plot_surface(
X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('jet'),
linewidth=0, antialiased=False, alpha=0.5 )
plt.title(r"$\sum_m|Y^m_4|^2$")
# below are codes copied from stackoverflow, to make the scaling correct
max_range = np.array([X.max()-X.min(), Y.max()-Y.min(), Z.max()-Z.min()]).max() / 2.0
mid_x = (X.max()+X.min()) * 0.5
mid_y = (Y.max()+Y.min()) * 0.5
mid_z = (Z.max()+Z.min()) * 0.5
ax.set_xlim(mid_x - max_range, mid_x + max_range)
ax.set_ylim(mid_y - max_range, mid_y + max_range)
ax.set_zlim(mid_z - max_range, mid_z + max_range)
#help(ax)
#ax.view_init(elev=30,azim=0) #调节视角，elev指向上(z方向)旋转的角度，azim指xy平面内旋转的角度
#plt.legend(r"$|Y_{lm}|^2$")
plt.show()
（颜色没有物理意义，只是方便观看），
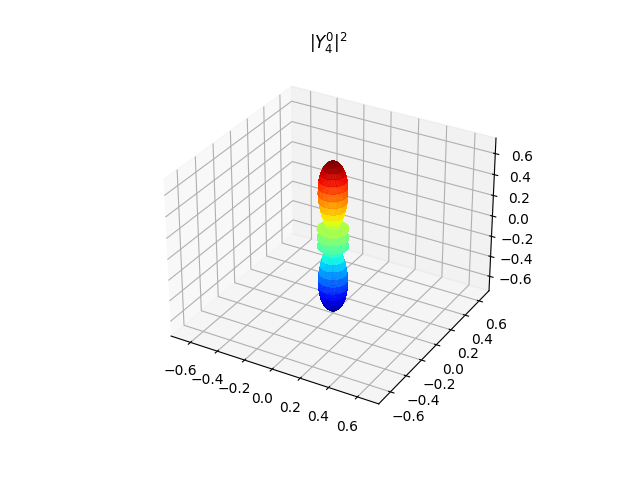
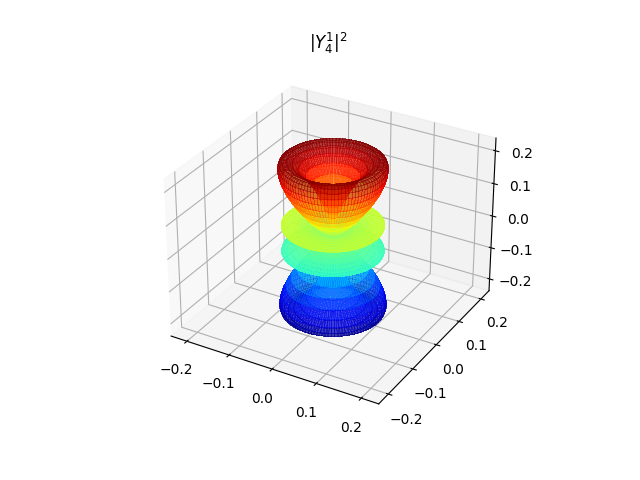
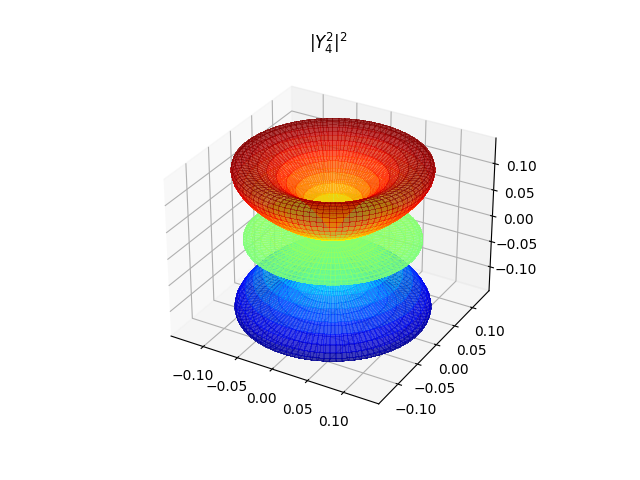
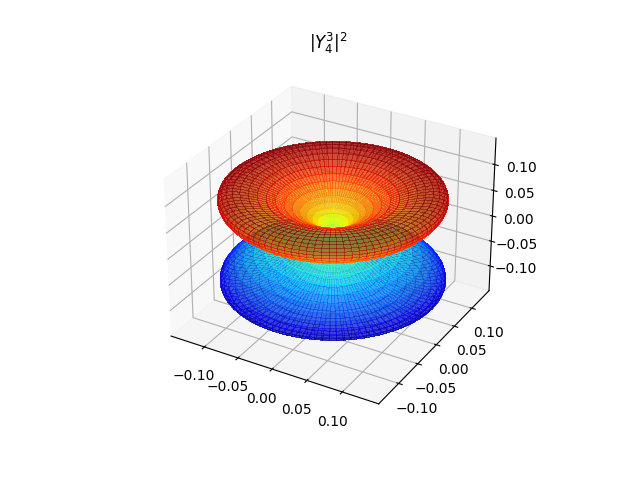
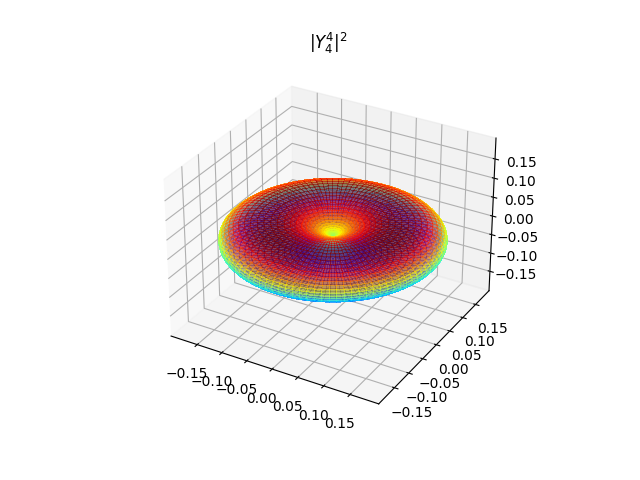
\(|Y^0_4|^2\) 是杆状，其他都是环状，\(|Y^1_4|^2~~ \rightarrow~~ |Y^4_4|^2\) 的环结构越来越简单，直到 \(|Y^4_4|^2\) 是一个甜甜圈。
结合 \(|r R_{nl}(r)|^2\) 的图，可以得到结论：
- \(\psi_{540}\) 的几率分布大致呈哑铃形—— \(z\) 方向两端几率较多，在 \(r\) 上有\(1\) 个极大值点。
- \(\psi_{541} ~~ \rightarrow \psi_{544}\) 的几率呈环状，如果按照 \(R_{nl}\) 的信息大致地认为有一层几率球壳，那么 \(Y^m_l\) 的影响是：球壳上有几个纬度是几率较大的，即有几个环结构，最简单的是 \(\psi_{544}\)——赤道上有一个几率环结构。
可以粗略地想象，密度球壳上，不同 \(m\) 值对应不同纬度的部分。
值得检查的想法：电子波函数中存在环绕 \(\vec{e}_z\) 的几率流，如果几率流的流速差不多，在赤道上的几率流会导致更大的 \(L_z\) 角动量。那么总角动量如何体现在这个经典图像中呢？
如果所有 \(m\) 轨道都占满，角向几率分布如下：
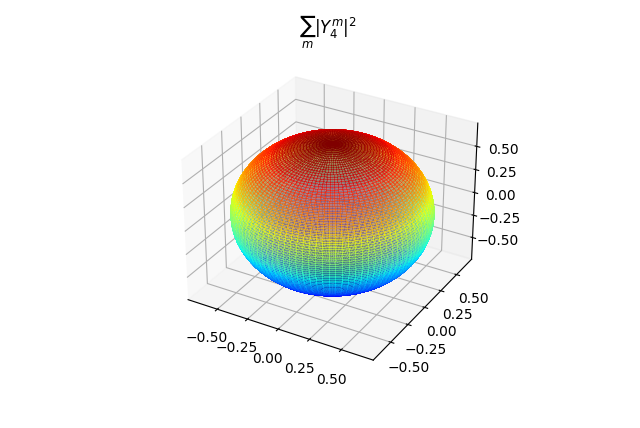
即几率呈球形分布，具有转动对称性，这是合理的（根据转动算符可以推断）。
2. 原子核高-j 轨道的几率分布
原子核中不是库仑势，我们相信更接近于 Woods-Saxon 势，但 \(l\) 仍然是好量子数，所以角向的几率分布是相同的。
径向会有些区别，但是同样是有 \(n_r\) 个极大值。所以上面对氢原子轨道的几率分布的定性讨论，对原子核中也是适用的。
只是，还需要考虑轨道自旋耦合。
任何一个 \((nljm)\) 轨道，都是几个 \((nl m_l)\) 轨道的线性叠加，密度也相应做叠加。
除了最小的 \(m\)，其他都是类环状结构。
如果是空穴，可以想象密度球壳上少了一块，如果是少了中间的一块，剩下的是一个哑铃形状。
