python 打靶法求解薛定谔方程

（未经允许，不得转载）

对于常微分方程边值问题/本征值问题，打靶法应该不是最稳定的算法，但是可能是最简单的算法。

图个简单，不妨用用打靶法。这里求解几个量子力学问题。

参考文献：

[1] Morten Hjorth-Jensen, "Computational Physics Lecture Notes Fall 2015"

[2] B. Alex Brown, "Lecture Notes in Nuclear Structure Physics"

[3] 马红儒，“计算物理讲义”

1. 热身：打靶法求解一维谐振子薛定谔方程

1.1 理论公式

一维谐振子薛定谔方程：

\[-\frac{\hbar^2}{2m} \frac{ d^2 }{d x^2} \psi(x) + \frac{1}{2}m \omega^2 x^2 \psi(x) = E \psi(x). \]

即

\[\frac{d^2}{dx^2} \psi(x) = [\frac{ m^2 \omega^2 x^2}{\hbar^2} - \frac{2mE}{\hbar^2} ] \psi(x). \]

可以设计一个长度量 \(x_0 = \sqrt{\hbar/(m\omega)}\)，然后整理方程，可以取 \(t = x/x_0\)，\(E'=E/(\hbar \omega/2)\), \(\Phi(t) = \psi(t x_0)\)，则可以把上面的方程整理为

\[\frac{ d^2 }{dt^2} \Phi(t) = (t^2 - E')\Phi(t), \]

这样整个方程中没有量纲，比较干净。我们知道，偶宇称解为 \(E' = 1, 5, 9, \cdots\)；奇宇称解为 \(E' = 3, 7, 11, \cdots\)。

1.2 代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import fsolve

# 一维谐振子： Phi''(t) = (t^2 - E' ) Phi(t)
def deriv(y,t,EE): # EE 即 E' = E/(hbar omega /2 )
    return [y[1], (t*t - EE) * y[0]]
    # y[0] 是 Phi, y[1] 是 Phi', 所以 [Phi, Phi'] 的导数是：
    # [Phi', Phi''] = [Phi', (t*t-E') Phi ]

tmax = 10; n = 1000
def shoot( EE): # 从 tmax 往　t=0 打靶
    t1 = np.linspace(tmax, 0, n); # 生成横坐标，从大到小
    sol1 = odeint(deriv, [1E-10, 0], t1, args=(EE,)) # ODE 从右往左推
    return sol1[-1,0] # 想要偶宇称，就打 sol1[-1,1]; 想要奇宇称，就打 sol1[-1,0]

root = fsolve(shoot, [-0.5]) # 得到本征能量
print("root=",root," shoot(root)=",shoot(root))

# 画个图，显示 [0, tmax] 上的波函数
t1 = np.linspace(tmax, 0, n); 
sol1 = odeint(deriv, [1E-10, 0], t1, args=(root,))
plt.plot(t1, sol1[:,0], label = "sol1"); plt.show();

代码思路：

  • 选定 \(t=10\) 的点，取值 \(\Phi(10) = 10^{-10}, \Phi'(10) = 0\)。
  • 调用 odeint 函数从 \(t=10\) 往 \(t=0\) 推；如果想要偶宇称解，就打靶 \(\Phi'(0)\)；如果想要奇宇称解，就打靶 \(\Phi(0)\)。
  • 理论上分析可知，无穷远处渐进解为 \(e^{r^2/2}, e^{-r^2/2}\) 的线性叠加，所以数值求解时，这两个组分都会混进来。如果从 \(t=0\) 往 \(t=10\) 推，\(e^{r^2/2}\) 相关的解就会被迅速放大，得到非物理的解。而从右往左推，这个组分就会很小，只剩下 \(e^{-r^2/2}\) 相关的物理的解。
  • 打靶即调节 \(E'\)，使得 \(\Phi'(0) \approx 0\)(偶宇称)，或者 \(\Phi(0) \approx 0\) （奇宇称）。

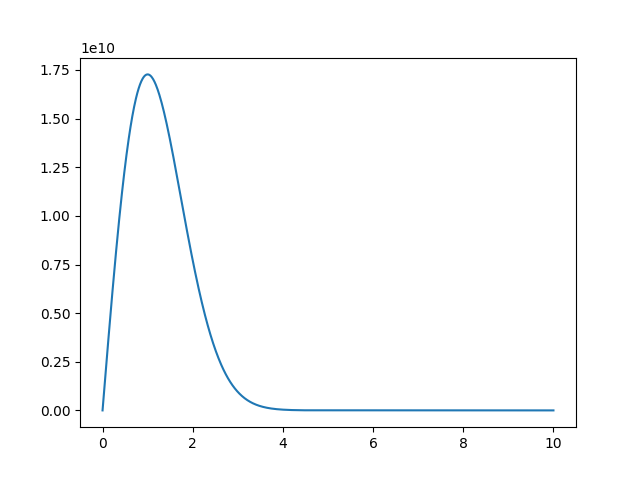
运行结果（以奇宇称第一激发态为例）：

root= [3.00000002]  shoot(root)= 0.0002180337905883789

image

2. 打靶法求解氢原子径向方程

2.1 理论公式

三维薛定谔方程：

\[- \frac{ \hbar^2 }{2m} \nabla^2 \psi(\vec{r}) + V(r) \psi(\vec{r}) = E \psi(\vec{r}), \]

代入 \(\psi(\vec{r}) = R(r) Y(\theta, \phi)\)，取 \(u(r) = R(r) / r\)，得到径向方程：

\[\frac{d^2}{dr^2}u(r) = [ \frac{-2m(E-V)}{\hbar^2} + \frac{l(l+1)}{r^2} ]u(r) \]

然后定义 \(\Kappa = \frac{ \sqrt{-2mE}}{\hbar}\), \(\rho = \Kappa r\), 可以将上面的方程整理为

\[\frac{d^2}{d \rho^2} u(\rho/K) = [ 1 - \frac{V(\rho/K)}{E} + \frac{l(l+1)}{\rho^2} ]u(\rho/K) \]

这个式子对于任意中心势都成立，

取　$\rho_0 = \frac{me^2}{4\pi \epsilon_0 \hbar^2 K} $，可以把径向方程整理为

\[\frac{d^2}{d \rho^2} u(\rho/K) = ( 1 - \frac{ 2\rho_0 }{\rho} + \frac{l(l+1)}{\rho^2})u(\rho/K). \]

理论上 \(\rho_0 = n = l+1, l+2, \cdots\)，相应地，本征能量为

\[E_n = - \frac{ me^4}{32 \pi^2 \epsilon^2_0 \hbar^2} \frac{1}{n^2} = - 13.6 eV \frac{1}{n^2}. \]

2.2 代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import fsolve

# 氢原子径向方程： u''(rho) = (1 - rho0/rho + l(l+1)/rho/rho ) u(rho)
def deriv(y,rho, rho0, l):
    return [y[1], (1 - 2*rho0/rho + l*(l+1)/rho/rho ) * y[0]]
    # y[0] 是 u, y[1] 是 u', 所以 [u, u'] 的导数是：
    # [u', u''] = [u', (1 - rho0/rho + l(l+1)/rho/rho ) u ]

rhomax = 50; n = 1000; l = 2
def shoot( rho0 ): # 从 tmax 往　t=0 打靶
    rho = np.linspace(rhomax, 1E-3, n); # 生成横坐标，从大到小
    sol1 = odeint(deriv, [1E-10, 0], rho, args=(rho0, l)) # ODE 从右往左推
    return sol1[-1,0] # u(r) = R(r) / r，要使得 R(0) 为有限大的数，u(0) = 0

root = fsolve(shoot, [2.5]) # 得到本征能量
print("root=",root," shoot(root)=",shoot(root))

# 画个图，显示 [0, tmax] 上的波函数
rho = np.linspace(rhomax, 1E-3, n);
sol1 = odeint(deriv, [1E-10, 0], rho, args=(root,l))
plt.plot(rho, sol1[:,0], label = "sol1"); plt.savefig("氢原子径向波函数.png"); plt.show();

代码思路：

  • 从 \(\rho = 50\) 往 \(\rho=0\) 推，边界条件为 \(u(0) = 0\)。
  • 因为微分方程中有 \(\rho^{-1}, \rho^{-2}\) 项，如果取值 \(\rho=0\) 会存在数值问题，所以打靶目标为 \(u(10^{-3}) \approx 0\)。
  • 无穷远处有 \(e^\rho, e^{-\rho}\) 两个渐进解，所以从右往左推，可以抑制 \(e^\rho\) 相关组分，剩下较为物理的解。
  • $ \rho \rightarrow 0$ 有 \(\rho^{-l}, \rho^{l+1}\) 两个渐进解，似乎前一个被抑制了，我觉得可能是因为从右往左推时，在 \(\rho \rightarrow 0\) 附近波函数的值比较大，而 \(\rho^{-l}\) 比较小。
  • \(n = l+1, l+2, \cdots\)。如果要得到 \(n\) 值较大的能级，可能需要调大 rhomax。

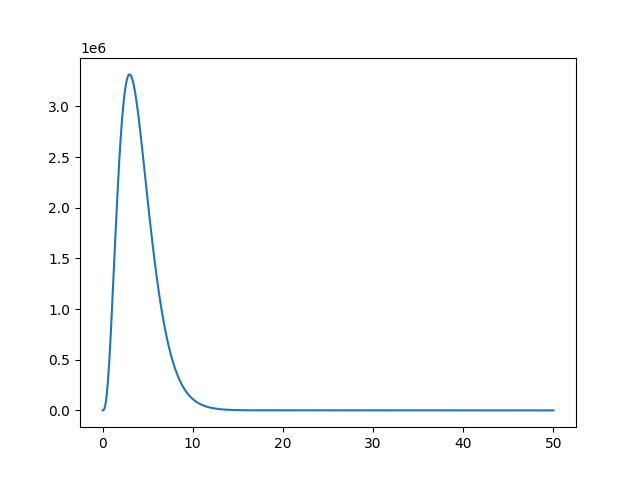
运行结果：

root= [2.99999998]  shoot(root)= -3.519999693543761

能级很准确。

image

3. Woods-Saxon 势

3.1 薛定谔径向方程

Again, 三维薛定谔方程：

\[- \frac{ \hbar^2 }{2m} \nabla^2 \psi(\vec{r}) + V(r) \psi(\vec{r}) = E \psi(\vec{r}), \]

代入 \(\psi(\vec{r}) = R(r) Y(\theta, \phi)\)，取 \(u(r) = R(r) / r\)，得到径向方程：

\[\frac{d^2}{dr^2}u(r) = [ \frac{-2m(E-V)}{\hbar^2} + \frac{l(l+1)}{r^2} ]u(r) \]

然后定义 \(\Kappa = \frac{ \sqrt{-2mE}}{\hbar}\), \(\rho = \Kappa r\), 可以将上面的方程整理为

\[\frac{d^2}{d \rho^2} u(\rho/K) = [ 1 - \frac{V(\rho/K)}{E} + \frac{l(l+1)}{\rho^2} ]u(\rho/K). \]

这个式子对于任意中心势都成立。把 $E = - \frac{ \hbar^2 K^2}{2m} = $ 代入，然后以 \(K\) 为参数进行打靶，由于 \(\frac{\hbar^2}{2m} \frac{ fm^{-2}}{MeV} = 19.4\)，即 \(-E/MeV = 19.4 (K/fm^{-1})^2\)，所以可以写成

\[\frac{d^2}{d \rho^2} u(\rho/K) = [ 1 + \frac{V(\rho/K)}{19.4 K^2} + \frac{l(l+1)}{\rho^2} ]u(\rho/K)． \]

3.2 Woods-Saxon 势参数

Woods-Saxon 势的定义如下[2]，

\[V(r) = V_o(r) + V_{so}(r) \vec{l} \cdot \vec{s} + V_c(r), \]

这里 \(V_o(r)\) 是自旋无关的中心势，有个费米函数形状，我还不清楚这个费米函数形状是如何 reasoning，

\[V_o(r) = V_o f_o(r) = \frac{ V_o }{ 1 + e^{\frac{r-R_o}{a_o}} } , \]

而 \(V_{so}(r)\) 是自选轨道耦合相互作用，据说是 Fermi 建议 Meyer 考虑，

\[V_{so}(r) = V_{so} \frac{1}{r} \frac{ d f_{so}(r) }{dr} = V_{so} \frac{1}{r} \frac{ d }{dr } \frac{1}{ 1 + e^{\frac{r-R_{so}}{a_{so}}}}, \]

另外还可以考虑库伦相互作用，这里暂时没有考虑，如果需要可以参考 Ref. [2] 113 页。此外还可以考虑质子、中子的平均场不同，也可以参考 Ref.[2]。

我用的 Ref. [2] 里给的参数：

\[V_o = -53 MeV, ~~~ r_o = 1.25 fm, ~~~ R_o = r_o A^{1/3}, ~~~ a_o = 0.65 fm, \\ V_{so} = 22 MeV, ~~~ r_{so} = 1.25 fm, ~~~ R_{so} = r_{so} A^{1/3}, ~~~ a_{so} = 0.65 fm. \]

3.3 打靶法代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import fsolve

Vo = -53; r0 = 1.25;  ao = 0.65;
Vso = 22; rso = 1.25;  aso = 0.65;
def V(r, l, j, A):
    Ro = r0 * np.power(A, 1.0 / 3); Rso = rso * np.power(A, 1.0/3);
    return Vo * np.exp( -(r-Ro)/ao ) / ( 1 + np.exp( -(r-Ro)/ao )) - Vso * rso * rso / r * np.exp( (r - Rso)/aso ) / np.power( 1 + np.exp( (r-Rso)/aso ), 2) / aso * (j*(j+1)-l*(l+1)-0.75)/2

# 径向方程： u''(rho) = (1 - V(rho * rho0 ) / E + l(l+1)/rho/rho ) u(r), rho0 =  hbar / sqrt(-2mE) = 27.67 / sqrt(-E) fm
def deriv(y,rho,K,l,j,A):
    return [y[1], (1 + V(rho / K, l, j, A ) /19.4/K/K + l*(l+1)/rho/rho ) * y[0]]
    # y[0] 是 u, y[1] 是 u', 所以 [u, u'] 的导数是：
    # [u', u''] = [u', (1 - V(r)/E + l(l+1)/r/r ) u ]

def shoot( K, l, j, A ):
    rhomax = 20; n = 1000;
    rho = np.linspace(rhomax, 1E-2, n); # 生成横坐标，从大到小，往 u(1E-2) 打靶
    sol1 = odeint(deriv, [1E-10, 0], rho, args=(K, l, j, A)) # ODE 从右往左推，右端边界条件　u(rhomax) = 1E-10, u'(rhomax)=0
    return sol1[-1,0] # 返还 u(1E-2) 值，希望它为 0。不做 u(0) 是因为公式里会有 1/0 的情况出现

def Eig( k0, l, j, A ):
    return fsolve(shoot, [k0], args = (l, j, A)) # 从 k = k0 出发，让 fsolve 自己去找 k 值

'''
# 画一个 u(1E-2) ~ k 的图，可以目测一下存在几根束缚态轨道
k = np.linspace(0.5, 1.5, 100)
Delta_u = [ shoot(it, 0, 0.5, 130) for it in k ]
plt.plot(k, Delta_u); plt.show()
'''
AA = np.arange(60, 200, 1) # 例子：观察 g9/2, g7/2 劈裂，A = [60, 200)
E = [ -19.4 * (Eig( 2, 4, 4.5, it )**2) for it in AA ]; plt.plot(AA, E, label="0g9/2" );
E = [ -19.4 * (Eig( 2, 4, 3.5, it )**2) for it in AA ]; plt.plot(AA, E, label="0g7/2" );
plt.legend(); plt.show()

跑了一两分钟，得到 0g9/2, 0g7/2 轨道劈裂，感觉是对的，见下图。

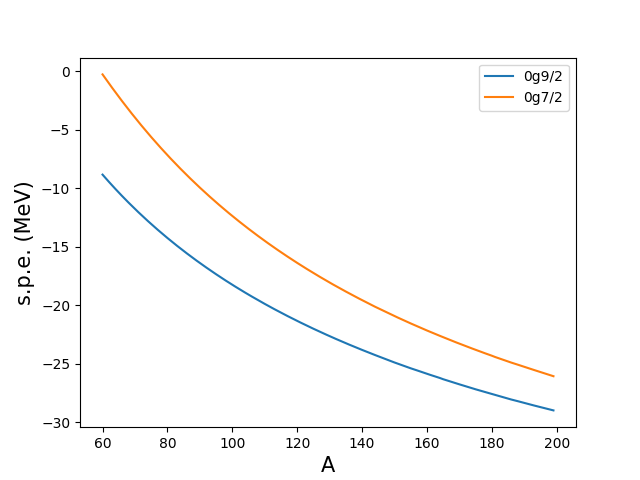
image

代码思路与氢原子几乎一致。此外我还有一个抱怨：

  • 对于给定的 \(l, j, A\)，有时候有多根轨道，用 fsolve 选不同的初值来得到，但是可能得手动选，不能像上图一样，选定初值 \(k_0 = 2\)，然后让 \(A\) 从 \(60\) 扫到 \(200\)，不是特别方便。但为了简洁性，这个代码先放在这里吧。

posted on 2022-10-02 01:02  luyi07  阅读(1016)  评论(0)  编辑  收藏  举报

导航